Численное решение нелинейных уравнений
Пусть дано нелинейное уравнение
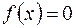, (20)
корни которого необходимо найти.
Допустим, что известен интервал [a,b], на котором непрерывная функция f(x) меняет знак (рис. 6). В этом случае можно считать, что известно приближенное решение уравнения x=(a+b)/2 с погрешностью, оценкой которой служит полуширина интервала неопределенности D(0)=|b-a|/2.
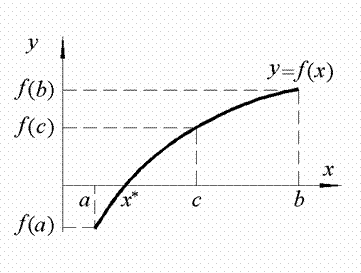
Рис. 6. Решение нелинейного уравнения
Метод бисекций
Метод бисекций (дихотомии, половинного деления) заключается в вычислении значения функции в середине отрезка [a,b], сравнении его знака со знаком функции, например, в точке а и отбрасывании той половины отрезка [a,b], на концах которой функция имеет одинаковые знаки. Далее это повторяется до тех пор, пока оценка погрешности D(k)=|b(k)-a(k)|/2 не станет меньше заданного числа e.
Алгоритм решения задачи может выглядеть следующим образом:
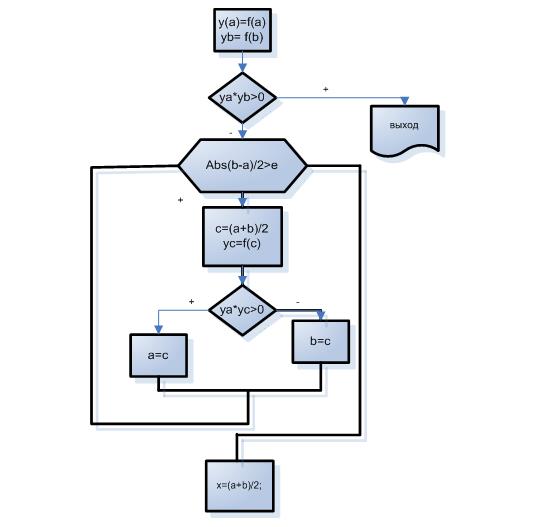
Метод простых итераций
Приведем (20) к виду
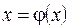, (21)
например, выбрав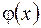 
в виде: 
.
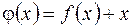Выберем начальное приближение x(0). Тогда можно организовать итерационный процесс по правилу
,
,
………………
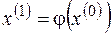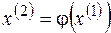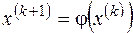, (22)
………………
Условие сходимости итерационного процесса записывается в виде неравенства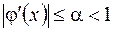 
(предполагая существование производной 
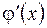в области поиска).
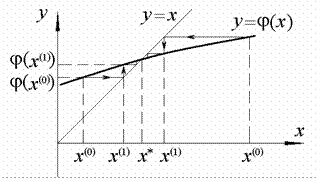
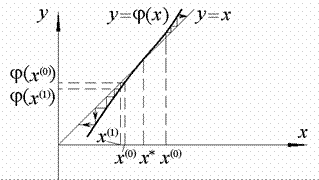
Процесс сходимости приближенного решения к точному иллюстрируется на рис. 7,а.
Условие сходимости a<1 является существенным, т.е. при a³1 имеет место расходимость (см. рис. 7,б).
 |  |
| а | б |
Рис. 7. Решение нелинейного уравнения методом простых итераций:
а сходимость при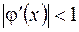 
, б расходимость при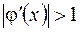 
Метод Ньютона (касательных)
Допустим, что функция f(x) непрерывно дифференцируема. Метод Ньютона заключается в построении касательной к графику функции y=f(x) в точке x=x(0), определению точки пересечения касательной с осью абсцисс, которая считается следующим приближением x(1), построению касательной в этой точке и т.д.
(рис. 8).
Используем уравнение касательной, проведенной в точке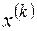 
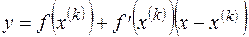(23)
и условие пересечения графиком касательной оси абсцисс (y=0), найдем
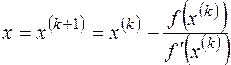. (24)
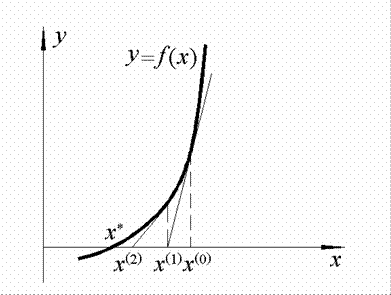
Рис.8. Метод Ньютона
Метод хорд (секущих)
Недостаток метода Ньютона связан с необходимостью вычисления производной. Однако производную можно приближенно вычислять конечно-разностным способом. На графике это можно изобразить, отметив на кривой y=f(x) две точки при x=x(0), x=x(1) и проведя через них секущую до пересечения с осью абсцисс (рис. 9). Если x(0)и x(1) расположены с разных сторон от корня x*, то ось абсцисс пересекает хорда, соединяющая две точки кривой (рис. 9).
Уравнение секущей, проходящей через две точки (x(0),f(x(0))), (x(1),f(x(1)))
.
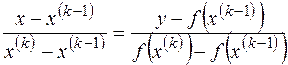Точка пересечения секущей с осью абсцисс (y=0) является следующим приближением решения уравнения
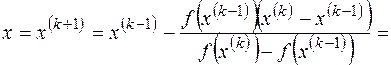
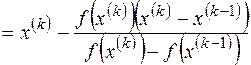. (25)
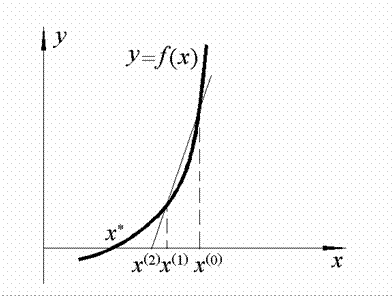
Рис. 9. Метод секущих (хорд)