Тема: Численное решение дифференциальных уравнений
Пусть дано дифференциальное уравнение первого порядка
 . (5.1)
. (5.1)
Требуется найти на отрезке 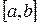 решение
решение  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию
 (5.2)
(5.2)
Будем предполагать, что условия теоремы существования и единственности выполнены. Для решения используем метод Эйлера (метод первого порядка точности, расчетные формулы (5.3)) и метод Рунге-Кутта (метод четвертого порядка точности, расчетные формулы (5.4)) с шагом h и 2h. Отметим, что результаты могут сильно отличаться, ввиду того, что метод Эйлера, имея только первый порядок точности, используется, как правило, для оценочных расчетов. Ориентировочную оценку погрешности метода Рунге-Кутта 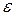 вычислить по формуле (5.5) [2].
вычислить по формуле (5.5) [2].
 , где h – шаг разбиения. (5.3)
, где h – шаг разбиения. (5.3)
 , где (5.4)
, где (5.4)

 .
.
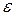 =
=  (5.5)
(5.5)
Задание 1
Написать программу решения дифференциального уравнения 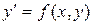 методом Эйлера на отрезке
методом Эйлера на отрезке 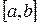 с шагом
с шагом 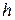 и 2h и начальным условием
и 2h и начальным условием 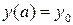 . Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.
. Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.
Задание 2
Написать программу решения дифференциального уравнения 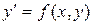 методом Рунге-Кутта на отрезке
методом Рунге-Кутта на отрезке 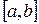 с шагом
с шагом 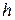 и 2h и начальным условием
и 2h и начальным условием 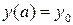 . Оценить погрешность по формуле (5.5). Исходные данные для выполнения задания берутся из таблицы 5.
. Оценить погрешность по формуле (5.5). Исходные данные для выполнения задания берутся из таблицы 5.
Примерный фрагмент выполнения лабораторной работы
1. Решить дифференциальное уравнение y’=f(x,y) методом Эйлера на отрезке [a,b] с шагом h c начальным условием y(a)=y0 , f(x,y)=(3x-y)/(x2+y), a=2, b=3, h=0.1, y0=1.
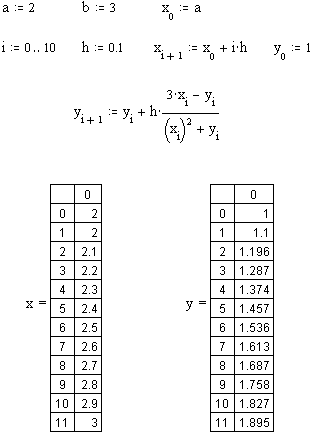
2. Решить дифференциальное уравнение y’=f(x,y) методом Рунге-Кутта на отрезке [a,b] с шагом h c начальным условием y(a)=y0.
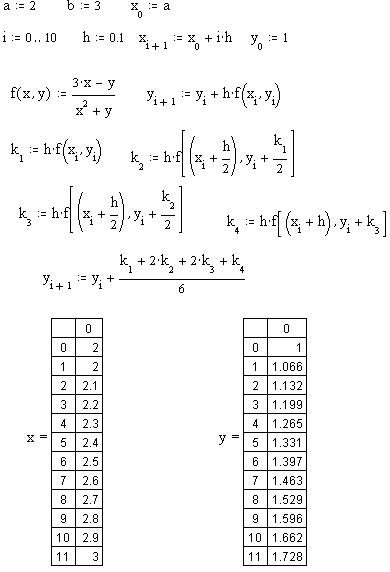
Таблица 5
| N | Функция | 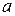 | 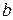 | 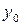 | 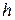 |
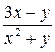  | 0.1 | ||||
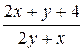 | 0.1 | ||||
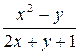 | 0.1 | ||||
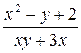 | 0.1 | ||||
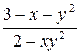 | 0.1 | ||||
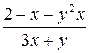 | 0.1 | ||||
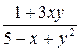 | 0.1 | ||||
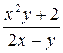 | 0.1 | ||||
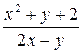 | 0.1 | ||||
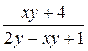 | 0.1 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Проверить для дифференциального уравнения условия теоремы существования и единственности.
2. На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений?
3. В какой форме можно получить решение дифференциального уравнения по методу Эйлера?
4. Каков геометрический смысл решения дифференциального уравнения методом Эйлера?
5. В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта?
6. Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и Рунге-Кутта?
7. Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?
Лабораторная работа №6
ТЕМА: Статистическая обработка опытных данных
Пусть зависимость между переменными  и
и  задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции
задана таблично (заданы опытные данные). Требуется найти функцию в некотором смысле наилучшим образом описывающую данные. Одним из способов подбора такой (приближающей) функции является метод наименьших квадратов. Метод состоит в том, чтобы сумма квадратов отклонений значений искомой функции  и заданной таблично
и заданной таблично  была наименьшей:
была наименьшей:
 (6.1)
(6.1)
где 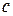 - вектор параметров искомой функции.
- вектор параметров искомой функции.
Задание 1
Построить методом наименьших квадратов две эмпирические формулы: линейную и квадратичную.
В случае линейной функции 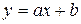 задача сводится нахождению параметров
задача сводится нахождению параметров 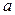 и
и 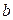 из системы линейных уравнений
из системы линейных уравнений
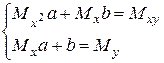 , где
, где
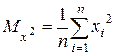 ,
, 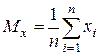 ,
, 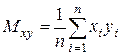 , My=
, My= 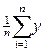 i
i
а в случае квадратичной зависимости 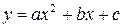 к нахождению параметров
к нахождению параметров 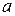 ,
, 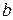 и
и 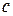 из системы уравнений:
из системы уравнений:
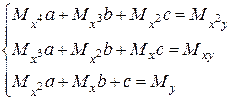 , где
, где
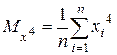 ,
, 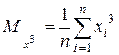 ,
, 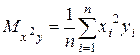
Выбрать из двух функций наиболее подходящую. Для этого составить таблицу для подсчета суммы квадратов уклонений по формуле (6.1). Исходные данные взять из таблицы 6.
Задание 2
Составить программу для нахождения приближающих функций заданного типа с выводом значений их параметров и соответствующих им сумм квадратов уклонений. Выбрать в качестве приближающих функций следующие: 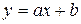 ,
, 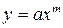 ,
, 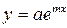 . Провести линеаризацию. Определить для какого вида функции сумма квадратов уклонений является наименьшей.
. Провести линеаризацию. Определить для какого вида функции сумма квадратов уклонений является наименьшей.
Исходные данные помещены в таблице 6.
Примерный фрагмент выполнения лабораторной работы
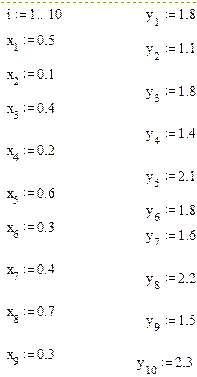
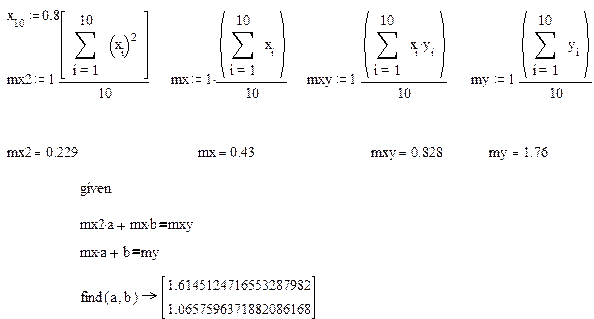
Таблица 6
  № № | |||||||||||
 | 0.5 | 0.1 | 0.4 | 0.2 | 0.6 | 0.3 | 0.4 | 0.7 | 0.3 | 0.8 | |
 | 1.8 | 1.1 | 1.8 | 1.4 | 2.1 | 1.8 | 1.6 | 2.2 | 1.5 | 2.3 | |
 | 1.7 | 1.5 | 3.7 | 1.1 | 6.2 | 0.3 | 6.5 | 3.6 | 3.8 | 5.9 | |
 | 1.5 | 1.4 | 1.6 | 1.3 | 2.1 | 1.1 | 2.2 | 1.8 | 1.7 | 2.3 | |
 | 1.7 | 1.1 | 1.6 | 1.2 | 1.9 | 1.5 | 1.8 | 1.4 | 1.3 | 1.0 | |
 | 6.7 | 5.6 | 6.7 | 6.1 | 7.4 | 6.9 | 7.9 | 5.9 | 5.6 | 5.3 | |
 | 1.3 | 1.2 | 1.5 | 1.4 | 1.9 | 1.1 | 2.0 | 1.6 | 1.7 | 1.8 | |
 | 5.5 | 5.9 | 6.3 | 5.8 | 7.4 | 5.4 | 7.6 | 6.9 | 6.6 | 7.5 | |
 | 2.3 | 1.4 | 1.0 | 1.9 | 1.5 | 1.8 | 2.1 | 1.6 | 1.7 | 1.3 | |
 | 5.3 | 3.9 | 2.9 | 5.0 | 4.0 | 4.9 | 5.1 | 4.5 | 4.1 | 3.7 | |
 | 1.8 | 2.6 | 2.3 | 1.3 | 2.0 | 2.1 | 1.1 | 1.9 | 1.6 | 1.5 | |
 | 4.4 | 6.4 | 5.3 | 3.7 | 4.9 | 5.6 | 3.0 | 5.0 | 4.3 | 3.7 | |
 | 1.9 | 2.1 | 2.0 | 2.9 | 3.0 | 2.6 | 2.5 | 2.7 | 2.2 | 2.8 | |
 | 6.6 | 7.6 | 6.7 | 9.2 | 9.4 | 7.8 | 8.4 | 8.0 | 7.9 | 8.7 | |
 | 2.0 | 1.4 | 1.0 | 1.7 | 1.3 | 1.6 | 1.9 | 1.5 | 1.2 | 2.1 | |
 | 7.5 | 6.1 | 4.8 | 7.4 | 5.7 | 7.0 | 7.1 | 6.8 | 6.0 | 8.9 | |
 | 2.0 | 1.2 | 1.8 | 1.9 | 1.1 | 1.7 | 1.6 | 1.4 | 1.5 | 1.3 | |
 | 7.5 | 5.9 | 7.0 | 8.0 | 5.0 | 7.4 | 6.4 | 6.6 | 6.3 | 5.7 | |
 | 1.9 | 1.1 | 1.4 | 2.3 | 1.7 | 2.1 | 1.6 | 1.5 | 1.0 | 1.2 | |
 | 4.7 | 3.4 | 3.8 | 5.2 | 4.6 | 5.5 | 3.9 | 3.9 | 3.2 | 3.5 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем суть приближения таблично заданной функции по методу наименьших квадратов?
2. Чем отличается этот метод от метода интерполяции?
3. Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции?
4. Может ли сумма квадратов уклонений для каких-либо приближающих функций быть равной нулю?
5. Какие элементарные функции используются в качестве приближающих функций?
6. Как найти параметры для линейной и квадратичной зависимости, используя метод наименьших квадратов?
Лабораторная работа №7
