Символьное решение систем уравнений
Фрагмент рабочего документа с соответствующими вычислениями приведен ниже. Здесь =- логическое равенство.
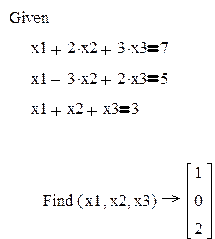 |
2. Решение системы линейных алгебраических уравнений как матричное уравнение Ax=b
Порядок выполнения задания.
1. Установите режим автоматических вычислений.
2. Введите матрицу системы и матрицу-столбец правых частей.
3. Вычислите решение системы по формуле x=A-1b.
4. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения.
5. Найдите решение системы с помощью функции lsolve и сравните результаты.
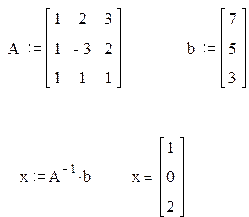 | 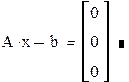 | ||
Решим систему с помощью функции lsolve и сравним результат с решением x=A-1b.
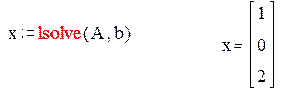 |
Решение линейной системы методом Гаусса
Комментарии. Функция augment(A,b) формирует расширенную матрицу системы добавлением к матрице системы справа столбца правых частей. Функция rref приводит расширенную матрицу системы к ступенчатому виду, выполняя прямой и обратный ходы гауссова исключения. Последний столбец содержит решение системы.
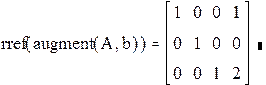 |
Решение системы методом Крамера
Порядок выполнения работы.
1. Вычисляем D определитель матрицы А.
2. Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1.
3. Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2.
4. Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3.
5. Определяем решение системы линейных уравнений x1, x2, x3.
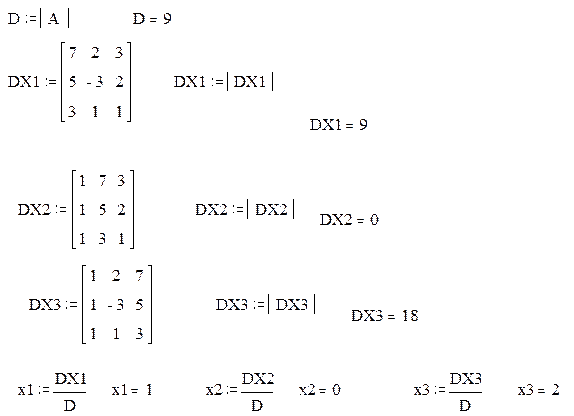 |
Решение системы линейных алгебраических уравнение методом простых итераций
Порядок выполнения задания
1. Введите матрицы C и d.
2. Преобразуйте исходную систему Cx=d к виду x=b+Ax.
3. Определите нулевое приближение решения.
4. Задайте количество итераций.
5. Вычислите последовательные приближения.
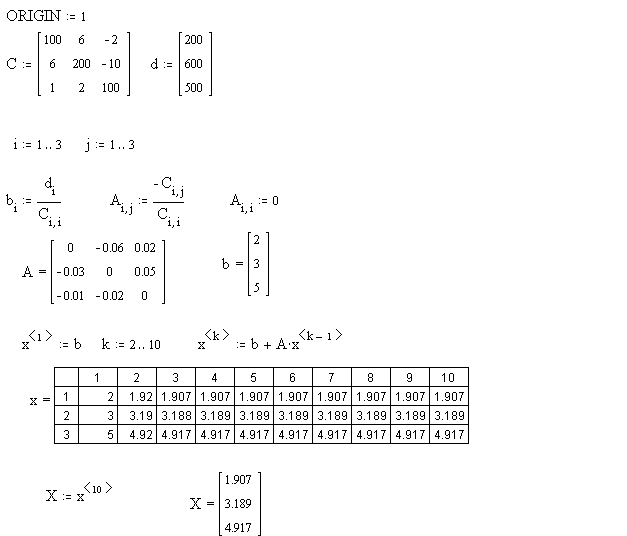
6.Решение системы линейных алгебраических уравнений методом Зейделя
Порядок выполнения задания
1. Введите матрицы С и d.
2. Преобразуйте систему Cx=d к виду x=b+A1x+A2x.
3. Определите нулевое приближение решения.
4. Задайте количество итераций.
5. Вычислите последовательные приближения.

Таблица 2
| № вар. |  | 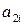 | 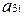 | 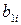 |
| 0.35 0.12 - 0.13 | 0.12 0.71 0.15 | - 0.13 0.15 0.63 | 0.10 0.26 0.38 | |
| 0.71 0.10 - 0.10 | 0.10 0.34 0.64 | 0.12 - 0.04 0.56 | 0.29 0.32 - 0.10 | |
| 0.34 - 0.04 0.06 | - 0.04 0.44 0.56 | 0.10 - 0.12 0.39 | 0.33 - 0.05 0.28 | |
| 0.10 - 0.04 - 0.43 | - 0.04 0.34 0.05 | - 0.63 0.05 0.13 | - 0.15 0.31 0.37 | |
| 0.63 0.05 0.15 | 0.05 0.34 0.10 | 0.15 0.10 0.71 | 0.34 0.32 0.42 | |
| 1.20 - 0.50 - 0.30 | - 0.20 1.70 0.10 | 0.30 - 1.60 - 1.50 | - 0.60 0.30 0.40 | |
| 0.30 - 0.10 - 1.50 | 1.20 - 0.20 - 0.30 | - 0.20 1.60 0.10 | - 0.60 0.30 0.70 | |
| 0.20 0.58 0.05 | 0.44 - 0.29 0.34 | 0.91 0.05 0.10 | 0.74 0.02 0.32 | |
| 6.36 7.42 1.77 | 1.75 19.03 0.42 | 1.0 1.75 6.36 | 41.70 49.49 27.67 | |
| 3.11 - 1.65 0.60 | - 1.66 3.15 0.78 | - 0.60 - 0.78 - 2.97 | - 0.92 2.57 1.65 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. К какому типу - прямому или итерационному - относится метод Гаусса?
2. В чем заключается прямой и обратный ход в схеме единственного деления?
3. Как организуется, контроль над вычислениями в прямом и обратном ходе?
4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?
5. Как формулируется достаточные условия сходимости итерационного процесса?
6. Как эти условия связаны с выбором метрики пространства?
7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?
Лабораторная работа №3
