Знакомство с системой MathCAD
Знакомство с системой MathCAD
Пользовательский интерфейс системы создан так, что пользователь, имеющий элементарные навыки работы с Windows-приложениями, может сразу начать работать с MathCAD.
Под интерфейсом понимается не только легкое управление системой, как с клавишного пульта, так и с помощью мыши, но и просто набор необходимых символов, формул, текстовых комментариев с последующим запуском документов (Worksheets) в реальном времени.
Запустив систему MathCAD из Windows, вы увидите на экране диалоговое окно, первоначально пустое (Рис. 1).
Рис. 1
Над ним видна строка с основными элементами интерфейса. Опции главного меню, содержащиеся в этой строке, легко изучит самостоятельно; некоторые из них очень похожи на стандартные опции, принятые в текстовых редакторах Windows.
Работа с документами MathCAD не требуют обязательного использования возможностей главного меню, так как основные из них дублируются кнопками быстрого управления, которые расположены в удобных перемещаемых с помощью мыши наборных панелях – палитрах. Наборные панели появляются в окне редактирования документов при активизации кнопок – пиктограмм. Они служат для вывода заготовок – шаблонов математических знаков (цифр, знаков арифметических операций, матриц, знаков интеграла, производных, приделов и др.). Указатель мыши подводим к “Вид” в главном меню, щелкаем левой кнопкой мыши; указатель подводим к “Панели инструментов” и щелкаем левой кнопкой мыши; Выпадает следующее меню. Указатель мыши подводим к “Математика” и щелкаем левой кнопкой мыши. Выпадают наборные панели. (Рис. 2)
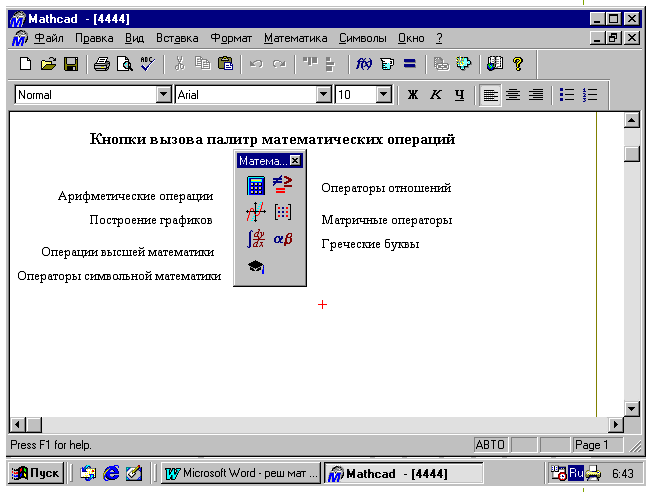
Рис. 2
Лабораторная работа №1
Задание 1
Сделать отделение корней: графически и по программе (точность 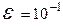 ). Индивидуальные задания приведены в таблице 1.
). Индивидуальные задания приведены в таблице 1.
Задание 2
1. Провести уточнение корней методом половинного деления.
В качестве начального приближения выберем 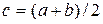 , затем исследуем функцию на концах отрезков
, затем исследуем функцию на концах отрезков 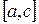 и
и 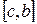 . Выбирается тот отрезок, у которого значение функции на концах имеет противоположные знаки. Процесс продолжается до тех пор, пока не выполнится условие
. Выбирается тот отрезок, у которого значение функции на концах имеет противоположные знаки. Процесс продолжается до тех пор, пока не выполнится условие 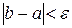 . Точность
. Точность 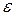 принять равной
принять равной 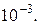
2. Сделать уточнение корней методом простой итерации.
Пусть корни отделены и 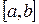 содержит единственный корень. Уравнение (1.1) приведем к итерационному виду:
содержит единственный корень. Уравнение (1.1) приведем к итерационному виду:
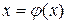 (1.2)
(1.2)
где функция 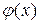 дифференцируема на
дифференцируема на 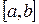 и для любого
и для любого 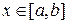
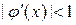 . Функцию
. Функцию 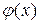 можно подобрать в виде
можно подобрать в виде
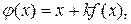 (1.3)
(1.3)
где 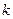 находится из условия
находится из условия 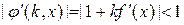 , для
, для 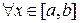 .
.
Последнее условие гарантирует сходимость итерационной последовательности 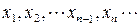 к корню
к корню 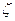 . Условием окончания счета будем считать выполнение неравенства
. Условием окончания счета будем считать выполнение неравенства
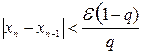
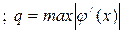 (1.4)
(1.4)
3. Сделать уточнение корней методом хорд или касательных (X, K в таблице 1) с заданной точностью 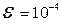 .
.
Расчетная формула для метода хорд:
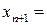
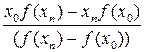 ,
,
для метода касательных:
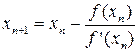 ,
,
Значение 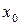 для метода хорд и начальная точка для метода касательных выбирается из условия выполнения неравенства
для метода хорд и начальная точка для метода касательных выбирается из условия выполнения неравенства 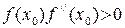 .
.
В результате вычислений по этим формулам может быть получена последовательность приближенных значений корня 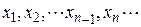 . Процесс вычислений заканчивается при выполнении условия
. Процесс вычислений заканчивается при выполнении условия 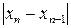 <
< 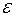 (
( 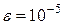 ). В каждом случае вывести на печать количество итераций, необходимых для достижения заданной точности.
). В каждом случае вывести на печать количество итераций, необходимых для достижения заданной точности.
Примерный вариант выполнения лабораторной работы на MathCad
1. Определение, построение таблиц значений и графиков функций и отделение корней уравнения y=x-sinx-0,25.
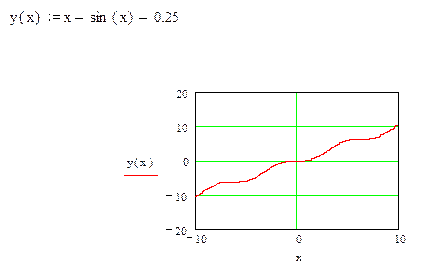 |
Отделяем корни графически.
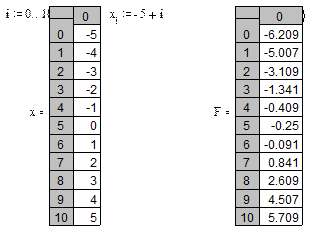 |
Вычисляем значения аргумента и функции.
Набираем i, xi Fi. Ниже, x= и рядом щелкаем мышью, набираем F= ,также рядом щелкаем мышью.
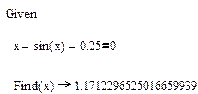 |
2. Решение с использованием операторов given, find.
3. Символьное решение.
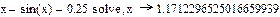 |
4. Слева решение методом итераций, посредине методом касательных, справа методом хорд.
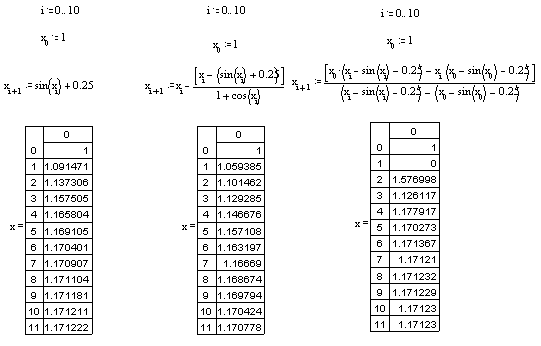
Таблица 1
| N | Метод | Уравнение |
| K | 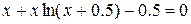 | |
| К | 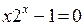 | |
| Х |  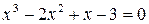 | |
| К | 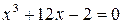 | |
| Х | 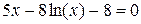 | |
| К | 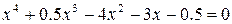 | |
| Х | 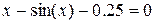 | |
| K | 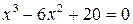 | |
| X | 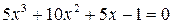 | |
| K | 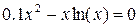 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Этапы решения уравнения с одной неизвестной.
2. Способы отделения корней.
3. Каким образом графическое отделение корней уточняется с помощью вычислений?
4. Дать словесное описание алгоритма метода половинного деления.
5. Необходимые условия сходимости метода половинного деления.
6. Условие окончания счета метода простой итерации. Погрешность метода.
7. Словесное описание алгоритма метода хорд. Графическое представление метода. Вычисление погрешности.
8. Словесное описание алгоритма метода касательных (Ньютона). Графическое представление метода. Условие выбора начальной точки.
Лабораторная работа №2
Задание 1
1. Решить систему линейных уравнений методом Гаусса. Задания приведены в таблице 2.
Комментарий. Контроль выполняемых вычислений является важным элементом решения любой вычислительной задачи. Для контроля прямого хода пользуются контрольными суммами, которые представляют собой суммы коэффициентов при неизвестных и свободного члена для каждого уравнения заданной системы.
Для контроля вычислений в основной части схемы единственного деления (столбцы коэффициентов при неизвестных и свободных членов) над контрольными суммами выполняют те же действия, что и над остальными элементами той же строки. При отсутствии вычислительных ошибок контрольная сумма для каждой строки в пределах влияниях погрешностей округления и их накопления должна совпадать со строчной суммой - вторым столбцом контроля. Строчные суммы представляют собой суммы всех элементов из основной части этой строки.
Задание 2
Решить систему (2.1) методом простой итерации. Предполагается в дальнейшем, что матрица А квадратная и невырожденная.
Предварительно приведем систему (2.2) к итерационному виду:
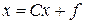 (2.3)
(2.3)
Для произвольного начального вектора 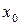 итерационный процесс
итерационный процесс
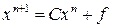
сходится, если выполнено одно из условий [2]
а) 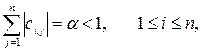 (2.4)
(2.4)
б) 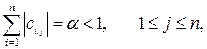 (2.5)
(2.5)
в) 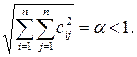 (2.6)
(2.6)
Процесс вычислений заканчиваем при выполнении условия
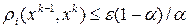 (2.7)
(2.7)
где 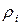 (i=1,2,3)- одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость,
(i=1,2,3)- одна из метрик, определяемая левой частью (2.4)-(2.6), по которой была установлена сходимость, 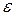 - заданная точность (
- заданная точность ( 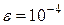 ).
).
Задание 3
Решить систему (2.1) методом Зейделя.
Метод Зейделя отличается от метода простой итерации тем, что найдя какое-то значение для компоненты, мы на следующем шаге используем его для отыскания следующей компоненты. Вычисления ведутся по формуле
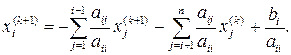 (2.8)
(2.8)
Каждое из условий (2.4)-(2.6) является достаточным для сходимости итерационного процесса по методу Зейделя. Практически же удобнее следующее преобразование системы (2.2). Домножая обе части (2.2) на АТ, получим эквивалентную ей систему
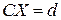 ,
,
где 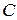 =
= 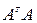 и d=
и d= 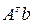 . Далее, поделив каждое уравнение на
. Далее, поделив каждое уравнение на 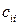 , приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.
, приведем систему к виду (2.8). Подобное преобразование также гарантирует сходимость итерационного процесса.
Примерный вариант выполнения лабораторной работы
Пример. Решите систему уравнений
X1+2X2+3X3=7,
X1-3X2+2X3=5,
X1+X2+X3=3.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. К какому типу - прямому или итерационному - относится метод Гаусса?
2. В чем заключается прямой и обратный ход в схеме единственного деления?
3. Как организуется, контроль над вычислениями в прямом и обратном ходе?
4. Как строится итерационная последовательность для нахождения решения системы линейных уравнений?
5. Как формулируется достаточные условия сходимости итерационного процесса?
6. Как эти условия связаны с выбором метрики пространства?
7. В чем отличие итерационного процесса метода Зейделя от аналогичного процесса метода простой итерации?
Лабораторная работа №3
Задание 1
По заданной таблице значений функции составить формулу интерполяционного многочлена Лагранжа (3.2) и построить график 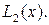 Исходные данные берутся из таблицы 3.1.
Исходные данные берутся из таблицы 3.1.
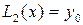
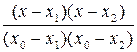 +
+ 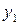
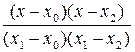 +
+ 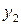
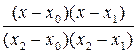 (3.2)
(3.2)
Tаблица 3.1.
| № | 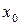 | 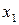 | 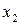 | 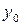 | 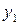 | 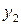 |
| -1 | -4 | |||||
| -2 | ||||||
| -3 | -1 | -1 | ||||
| -3 | -7 | |||||
| -2 | -1 | |||||
| -3 | ||||||
| -4 | -2 | |||||
| -1 | 1.5 | -7 | ||||
| -1 | -6 | |||||
| -9 | -7 | -4 | -3 | |||
| -1 | ||||||
| -7 | -5 | -4 | -4 |
Задание 2
Вычислить одно значение заданной функции для промежуточного значения аргумента ( 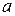 ) с помощью интерполяционного многочлена Лагранжа (3.3) и оценить погрешность интерполяции. Для выполнения задания исходные данные берутся из таблицы 3.2, 3.3 или 3.4.
) с помощью интерполяционного многочлена Лагранжа (3.3) и оценить погрешность интерполяции. Для выполнения задания исходные данные берутся из таблицы 3.2, 3.3 или 3.4.
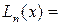
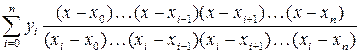 (3.3)
(3.3)
Для погрешности 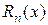 выполняется неравенство
выполняется неравенство
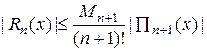 ,
, 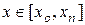 (3.4)
(3.4)
где 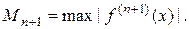
Таблица 3.2
| № варианта | Значение а | № таблицы |
| -2 | 3.3 | |
| 3.77 | 3.4 | |
| 0.55 | 3.3 | |
| 4.83 | 3.4 | |
| 3.5 | 3.3 | |
| 5.1 | 3.4 | |
| 1.75 | 3.3 | |
| 4.2 | 3.4 | |
| -1.55 | 3.3 | |
| 6.76 | 3.4 |
Таблица 3.3
 | -3.2 | -0.8 | 0.4 | 2.8 | 4.0 | 6.4 | 7.6 |
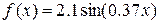 | -1.94 | -0.61 | 0.31 | 1.81 | 2.09 | 1.47 | 0.68 |
Таблица 3.4
 | 1.3 | 2.1 | 3.7 | 4.5 | 6.1 | 7.7 | 8.5 |
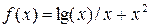 | 1.777 | 4.563 | 13.84 | 20.39 | 37.34 | 59.41 | 72.4 |
Таблица 3.5
 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 |
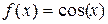 | 0.995 | 0.988 | 0.980 | 0.969 | 0.955 | 0.939 | 0.921 |
Таблица 3.6
 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 |
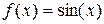 | 0.605 | 0.644 | 0.681 | 0.71 | 0.75 | 0.783 | 0.813 |
Задание 3.
Уплотнить часть таблицы заданной на отрезке 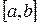 функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке
функции, используя интерполяционный многочлен Ньютона (3.5) и оценить погрешность интерполяции D (формула (3.6)). Таблицу 3.7 конечных разностей просчитать вручную на отрезке 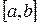 с шагом
с шагом 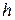 . Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
. Для выполнения задания исходные данные берутся из таблиц 3.8, 3.5 и 3.6.
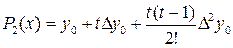 +
+ 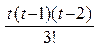
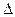 3y0, (3.5)
3y0, (3.5)
где 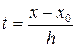 .
.
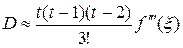 , (3.6)
, (3.6)
где 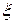 – некоторая внутренняя точка наименьшего промежутка, содержащего все узлы
– некоторая внутренняя точка наименьшего промежутка, содержащего все узлы 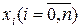 и x.
и x.
Формула (3.5) называется первой интерполяционной формулой Ньютона. Если вычисляемое значение переменной ближе к концу отрезка 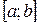 , то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).
, то применяют вторую формулу Ньютона – интерполирование назад (формула (3.6)).
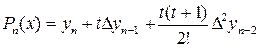 +
+ 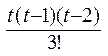

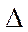 3yn-3 (3.6)
3yn-3 (3.6)
где 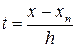 и
и 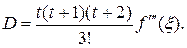
Таблица 3.7
 |  | 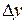 | 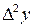 | 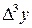 |
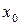 | 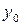 | 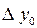 = = 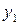 - - 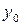 | 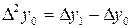 | 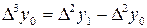 |
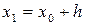 | 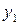 | 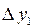 = = 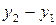 | 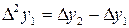 | |
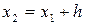 | 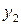 | 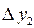 = = 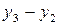 | ||
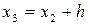 | 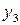 |
Таблица 3.8
| № | 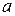 | 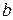 | 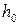 | 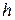 | № таблицы |
| 0.65 | 0.80 | 0.05 | 0.01 | 3.6 | |
| 0.25 | 0.40 | 0.05 | 0.025 | 3.5 | |
| 0.75 | 0.90 | 0.05 | 0.01 | 3.6 | |
| 0.70 | 0.85 | 0.05 | 0.025 | 3.6 | |
| 0.80 | 0.95 | 0.05 | 0.025 | 3.6 | |
| 0.1 | 0.25 | 0.05 | 0.025 | 3.5 | |
| 0.15 | 0.3 | 0.05 | 0.025 | 3.5 | |
| 0.7 | 0.85 | 0.05 | 0.025 | 3.6 | |
| 0.2 | 0.35 | 0.05 | 0.01 | 3.5 | |
| 0.80 | 0.95 | 0.05 | 0.01 | 3.6 |
Примерный фрагмент выполнения работы
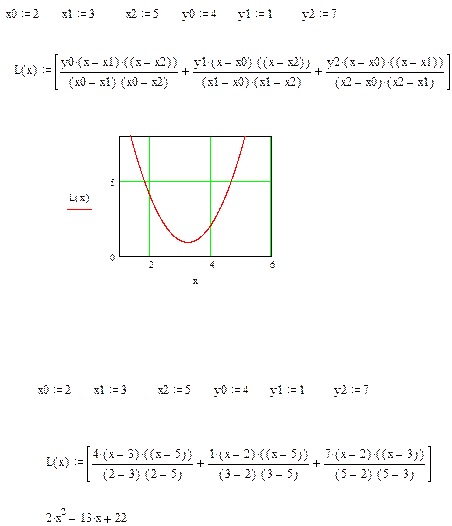
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем особенность приближения таблично заданной функции методом интерполирования?
2. Как обосновывается существование и единственность интерполяционного многочлена?
3. Как связана степень интерполяционного многочлена с количеством узлов интерполяции?
4. Как строятся интерполяционные многочлены Лагранжа и Ньютона?
5. В чем особенности этих двух способов интерполяции?
6. Как производится оценка погрешности метода интерполяции многочленом Лагранжа?
7. Как используется метод интерполирования для уточнения таблиц функций?
8. В чем отличие между первой и второй интерполяционными формулами Ньютона?
Лабораторная работа №4
Задание 1
Составить программу вычисления интеграла от заданной функции на отрезке 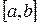 по формуле трапеций с шагом
по формуле трапеций с шагом 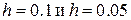 . Сравнить результаты. Оценить точность по формуле (4.3). Сравнить результаты. Исходные данные для выполнения задания берутся из таблицы 4.
. Сравнить результаты. Оценить точность по формуле (4.3). Сравнить результаты. Исходные данные для выполнения задания берутся из таблицы 4.
Задание 2
Составить программу вычисления интеграла от заданной функции на отрезке 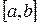 по формуле Симпсона методом повторного счета с точностью
по формуле Симпсона методом повторного счета с точностью 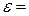 10-6. Исходные данные для выполнения задания берутся из таблицы 4.
10-6. Исходные данные для выполнения задания берутся из таблицы 4.
Примерный фрагмент выполнения лабораторной работы
Вычислить интеграл от заданной функции на отрезке [a,b] по формуле трапеций и прямым способом.
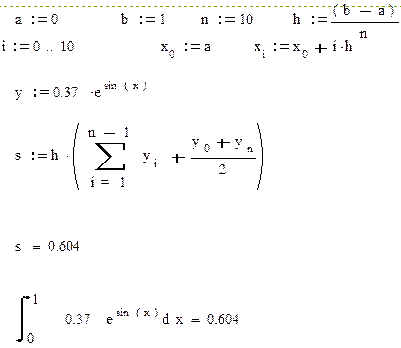 |
Таблица 4
| N | Функция | 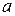 | 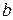 |
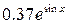 | |||
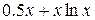 | |||
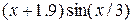 | |||
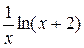 | |||
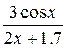 | |||
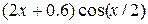 | |||
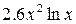 | 1.2 | 2.2 | |
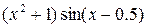 | |||
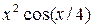 | |||
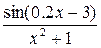 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Каковы преимущества формулы парабол по сравнению с формулой трапеций и следствием чего являются эти преимущества?
2. Верны ли формулы (4.2), (4.4) для неравноотстоящих узлов?
3. В каких случаях приближенные формулы трапеций и парабол оказываются точными?
4. Как влияет на точность численного интегрирования величина шага?
5. Каким способом можно прогнозировать примерную величину шага для достижения заданной точности интегрирования?
6. Можно ли добиться неограниченного уменьшения погрешности интегрирования путем последовательного уменьшения шага?
Лабораторная работа №5
Задание 1
Написать программу решения дифференциального уравнения 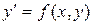 методом Эйлера на отрезке
методом Эйлера на отрезке 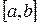 с шагом
с шагом 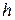 и 2h и начальным условием
и 2h и начальным условием 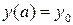 . Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.
. Исходные данные для выполнения задания берутся из таблицы 5. Сравнить результаты.
Задание 2
Написать программу решения дифференциального уравнения 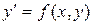 методом Рунге-Кутта на отрезке
методом Рунге-Кутта на отрезке 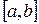 с шагом
с шагом 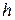 и 2h и начальным условием
и 2h и начальным условием 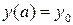 . Оценить погрешность по формуле (5.5). Исходные данные для выполнения задания берутся из таблицы 5.
. Оценить погрешность по формуле (5.5). Исходные данные для выполнения задания берутся из таблицы 5.
Примерный фрагмент выполнения лабораторной работы
1. Решить дифференциальное уравнение y’=f(x,y) методом Эйлера на отрезке [a,b] с шагом h c начальным условием y(a)=y0 , f(x,y)=(3x-y)/(x2+y), a=2, b=3, h=0.1, y0=1.
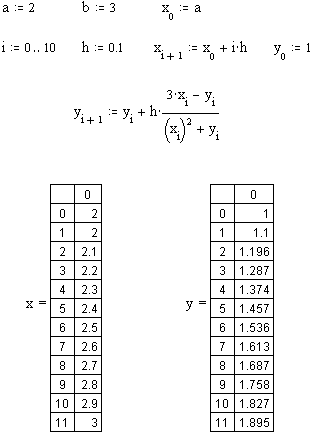
2. Решить дифференциальное уравнение y’=f(x,y) методом Рунге-Кутта на отрезке [a,b] с шагом h c начальным условием y(a)=y0.
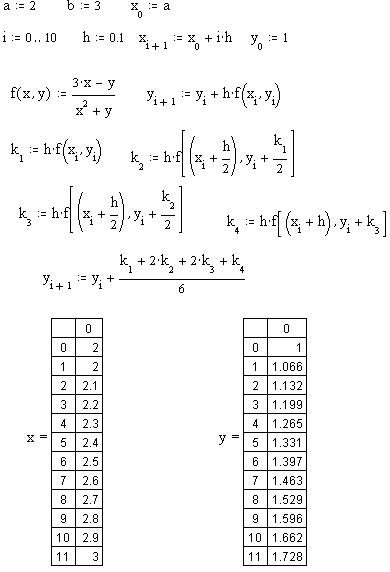
Таблица 5
| N | Функция | 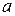 | 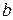 | 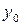 | 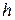 |
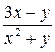  | 0.1 | ||||
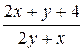 | 0.1 | ||||
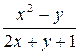 | 0.1 | ||||
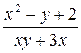 | 0.1 | ||||
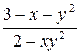 | 0.1 | ||||
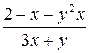 | 0.1 | ||||
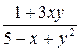 | 0.1 | ||||
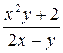 | 0.1 | ||||
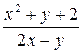 | 0.1 | ||||
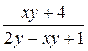 | 0.1 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Проверить для дифференциального уравнения условия теоремы существования и единственности.
2. На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений?
3. В какой форме можно получить решение дифференциального уравнения по методу Эйлера?
4. Каков геометрический смысл решения дифференциального уравнения методом Эйлера?
5. В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта?
6. Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и Рунге-Кутта?
7. Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?
Лабораторная работа №6
Задание 1
Построить методом наименьших квадратов две эмпирические формулы: линейную и квадратичную.
В случае линейной функции 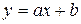 задача сводится нахождению параметров
задача сводится нахождению параметров 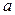 и
и 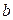 из системы линейных уравнений
из системы линейных уравнений
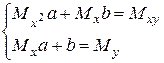 , где
, где
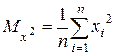 ,
, 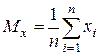 ,
, 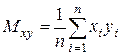 , My=
, My= 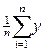 i
i
а в случае квадратичной зависимости 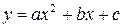 к нахождению параметров
к нахождению параметров 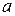 ,
, 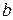 и
и 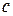 из системы уравнений:
из системы уравнений:
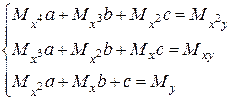 , где
, где
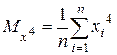 ,
, 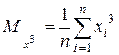 ,
, 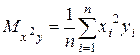
Выбрать из двух функций наиболее подходящую. Для этого составить таблицу для подсчета суммы квадратов уклонений по формуле (6.1). Исходные данные взять из таблицы 6.
Задание 2
Составить программу для нахождения приближающих функций заданного типа с выводом значений их параметров и соответствующих им сумм квадратов уклонений. Выбрать в качестве приближающих функций следующие: 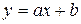 ,
, 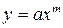 ,
, 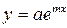 . Провести линеаризацию. Определить для какого вида функции сумма квадратов уклонений является наименьшей.
. Провести линеаризацию. Определить для какого вида функции сумма квадратов уклонений является наименьшей.
Исходные данные помещены в таблице 6.
Примерный фрагмент выполнения лабораторной работы
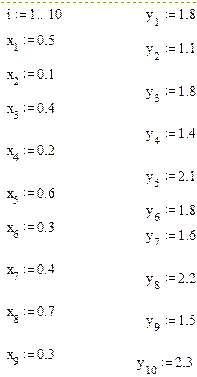
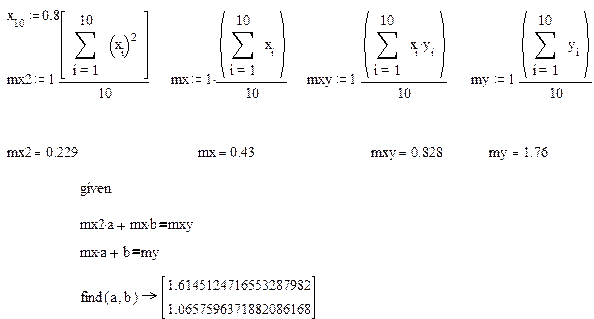
Таблица 6
  № № | |||||||||||
 | 0.5 | 0.1 | 0.4 | 0.2 | 0.6 | 0.3 | 0.4 | 0.7 | 0.3 | 0.8 | |
 | 1.8 | 1.1 | 1.8 | 1.4 | 2.1 | 1.8 | 1.6 | 2.2 | 1.5 | 2.3 | |
 | 1.7 | 1.5 | 3.7 | 1.1 | 6.2 | 0.3 | 6.5 | 3.6 | 3.8 | 5.9 | |
 | 1.5 | 1.4 | 1.6 | 1.3 | 2.1 | 1.1 | 2.2 | 1.8 | 1.7 | 2.3 | |
 | 1.7 | 1.1 | 1.6 | 1.2 | 1.9 | 1.5 | 1.8 | 1.4 | 1.3 | 1.0 | |
 | 6.7 | 5.6 | 6.7 | 6.1 | 7.4 | 6.9 | 7.9 | 5.9 | 5.6 | 5.3 | |
 | 1.3 | 1.2 | 1.5 | 1.4 | 1.9 | 1.1 | 2.0 | 1.6 | 1.7 | 1.8 | |
 | 5.5 | 5.9 | 6.3 | 5.8 | 7.4 | 5.4 | 7.6 | 6.9 | 6.6 | 7.5 | |
 | 2.3 | 1.4 | 1.0 | 1.9 | 1.5 | 1.8 | 2.1 | 1.6 | 1.7 | 1.3 | |
 | 5.3 | 3.9 | 2.9 | 5.0 | 4.0 | 4.9 | 5.1 | 4.5 | 4.1 | 3.7 | |
 | 1.8 | 2.6 | 2.3 | 1.3 | 2.0 | 2.1 | 1.1 | 1.9 | 1.6 | 1.5 | |
 | 4.4 | 6.4 | 5.3 | 3.7 | 4.9 | 5.6 | 3.0 | 5.0 | 4.3 | 3.7 | |
 | 1.9 | 2.1 | 2.0 | 2.9 | 3.0 | 2.6 | 2.5 | 2.7 | 2.2 | 2.8 | |
 | 6.6 | 7.6 | 6.7 | 9.2 | 9.4 | 7.8 | 8.4 | 8.0 | 7.9 | 8.7 | |
 | 2.0 | 1.4 | 1.0 | 1.7 | 1.3 | 1.6 | 1.9 | 1.5 | 1.2 | 2.1 | |
 | 7.5 | 6.1 | 4.8 | 7.4 | 5.7 | 7.0 | 7.1 | 6.8 | 6.0 | 8.9 | |
 | 2.0 | 1.2 | 1.8 | 1.9 | 1.1 | 1.7 | 1.6 | 1.4 | 1.5 | 1.3 | |
 | 7.5 | 5.9 | 7.0 | 8.0 | 5.0 | 7.4 | 6.4 | 6.6 | 6.3 | 5.7 | |
 | 1.9 | 1.1 | 1.4 | 2.3 | 1.7 | 2.1 | 1.6 | 1.5 | 1.0 | 1.2 | |
 | 4.7 | 3.4 | 3.8 | 5.2 | 4.6 | 5.5 | 3.9 | 3.9 | 3.2 | 3.5 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем суть приближения таблично заданной функции по методу наименьших квадратов?
2. Чем отличается этот метод от метода интерполяции?
3. Каким образом сводится задача построения приближающих функций в виде различных элементарных функций к случаю линейной функции?
4. Может ли сумма квадратов уклонений для каких-либо приближающих функций быть равной нулю?
5. Какие элементарные функции используются в качестве приближающих функций?
6. Как найти параметры для линейной и квадратичной зависимости, используя метод наименьших квадратов?
Лабораторная работа №7
Задание 1
Используя метод сеток, найти приближенное решение уравнения (7.1)-(7.3), удовлетворяющее условиям 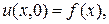
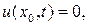
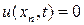 , для
, для 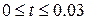 ,
, 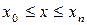 и h=0.1, l=0.005.
и h=0.1, l=0.005.
Решение должно быть оформлено в виде таблицы 7.1 подсчитанной вручную. Исходные данные заданы в таблице 7.2. Оценить погрешность вычислений по формуле (7.6).
Комментарий. Значения 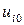 находим, подставляя значение хо в
находим, подставляя значение хо в 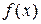 . Например,
. Например, 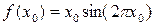 при
при 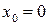 равна 0. Значения
равна 0. Значения 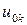 и
и 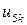 определяются краевыми условиями (в нашем случае нулевые). Далее значение, например,
определяются краевыми условиями (в нашем случае нулевые). Далее значение, например, 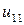 находим, используя формулу (7.5), т.е.
находим, используя формулу (7.5), т.е. 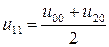 и т.д.
и т.д.
Таблица 7.1.
 j j |  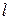 | 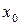 | 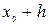 | 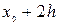 | 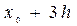 | 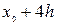 | 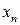 |
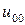 | 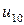 | 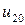 | 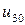 | 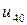 | 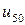 | ||
| 0.005 | 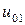 | 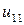 | 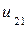 | 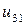 | 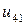 | 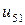 | |
| 0.010 | 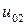 | 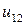 | 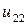 | 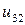 | 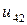 | 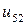 | |
| 0.015 | 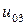 | 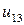 | 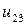 | 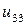 | 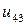 | 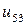 | |
| 0.020 | 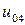 | 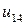 | 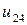 | 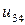 | 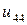 | 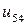 | |
| 0.025 | 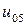 | 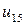 | < |
