Понятие и свойства тел вращения

Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости [2].

Выделяется несколько основных тел вращения:

Шар. Это геометрическая фигура, которая образована в результате вращения полукруга вокруг диаметра разреза [2].

Цилиндр. Это геометрическая фигура, которая образована в результате вращения прямоугольника вокруг одной из его сторон [2].

Конус. Это геометрическая фигура, которая образована в результате вращения прямоугольного треугольника вокруг одного из своих катетов [2].

Тор. Это геометрическая фигура, которая образована в результате вращения окружности вокруг прямой, при этом окружность прямую не пересекает[2].

Стоит отметить такой интересный факт, что если вращаются контуры фигур, то у нас возникает поверхность вращения. Пример – сфера, которая образовывается в результате вращения окружности. Если же вращаются заполненные контуры, то у нас возникают тела. Тела вращения, разумеется, имеют свой объем и свою площадь. И то и другое, можно узнать с помощью теорем Гульдина-Паппа.

Первая теорема гласит о том, что площадь поверхности линии, которая образуется при вращении и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению длины линии на длину окружности, пробегаемой центром масс этой линии.

Вторая теорема говорит о том, что объем тела, который образуется при вращении фигуры и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры [5].

Изучим более подробно тела:

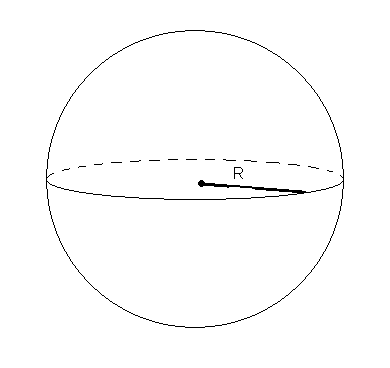
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки. Эта точка называется центром шара, а данное расстояние– радиусом шара[13].

Шар, так же как цилиндр и конус, является телом вращения.

Граница шара называется шаровой поверхностью или сферой. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом[13].

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом, а сечение сферы – большой окружностью[13].

Любая плоскость, проходящая через центр шара, является его плоскостью симметрии. Центр шара является его центром симметрии.

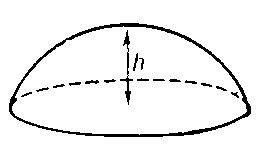
Шаровой сегмент – это часть шара, которая отсекается секущей плоскостью [13].

Шаровой сектор – это геометрическое тело, получающееся при вращении кругового сектора около одного из его радиусов [13].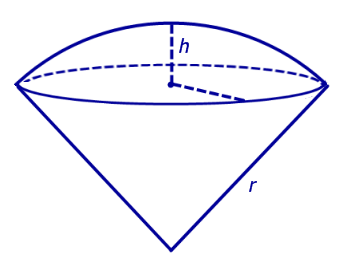

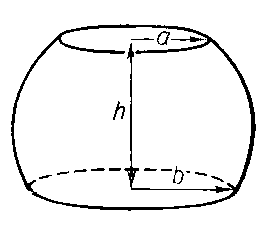Шаровой слой – часть шара, которая содержится между двумя параллельными плоскостями, пересекающими шар.

Основания шарового слоя это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями[13].

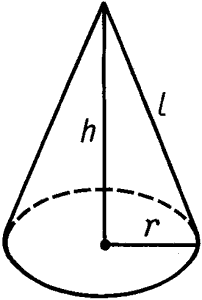Конус – тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.Поверхность конуса состоит из основания и боковой поверхности.Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.Конической поверхностью называется поверхность, образуемая движением прямой, проходящей всё время через неподвижную точку вдоль данной линии. Выделяется прямой конус.

Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называется осью прямого конуса [13].

У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

Конус называетсяпрямым круговым, если его направляющая – окружность, а вершина ортогонально проектируется в его центр.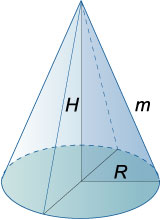

В элементарной геометрии прямой круговой конус часто называют просто конусом.

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса[13].

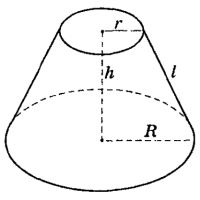Боковая поверхность прямого кругового конуса равна произведению половины длины окружности основания на образующую. Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус, гомотетичный данному, причём центром гомотетии служит вершина конуса.

Часть конуса, ограниченная его основанием и секущей плоскостью, параллельной основанию, называется усечённым конусом.

Цилиндрическая поверхность – поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению [13].

Бесконечный цилиндр – тело, ограниченное цилиндрической поверхностью.[13]

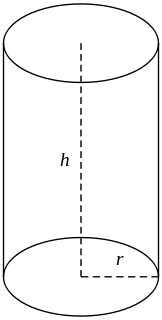
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра.

Высотой цилиндра называется расстояние между плоскостями его оснований.

Другая часть, ограниченная параллельными плоскостями – это основания цилиндра.У цилиндра:основания равны;образующие параллельны и равны.Боковая поверхность всякого цилиндра равна произведению образующей на периметр перпендикулярного сечения.Цилиндр, у которого основания перпендикулярны образующим и являются кругами, называется прямым круговым цилиндром (часто, и далее, – просто цилиндром).

Прямой круговой цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.Радиусом цилиндра называется радиус его основания. Осью цилиндра называется прямая, проходящая через центры его оснований. Ось цилиндра параллельна образующим.Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник [13].

Тор (от лат. torus — выпуклость), геометрическое тело, образуемое вращением круга вокруг не пересекающей его и лежащей в одной с ним плоскости прямой. Приблизительную форму тора имеет спасательный круг, баранка.Поверхность, ограничивающую тор, иногда также называют тором [2]. Площадь поверхности и объем тора вычисляются по теоремам Гульдина-Паппа. Если увеличить радиус трубы тора до тех пор, пока он не станет равен радиусу окружности, мы получим тор, в котором отсутствует центральное "отверстие". Такой тор называют пиковым тором. При дальнейшем увеличении радиуса трубы тор превращается в осевой тор. Внутренние "стенки" осевого тора пересекают друг друга, образуя в центре ось в виде веретена.Различают открытый тор, образованный вращением окружности вокруг оси, которая не пересекает образующую и закрытый тор, образованный вращением окружности вокруг оси, которая пересекает образующую окружность или касается ее[2].

В начальной школе знакомят с телами вращения. Дети изучают конус, цилиндр, шар. Изучение начинается с 1 класса. Например, с шаром детей знакомит учебник математики Рудницкой В.Н.. Во 2 классе информация присутствует во многих учебниках, как например Демидова Т.Е., Козлова С.А., Тонких А.П., Истомина А.И. и другие.

Таким образом, подводя итоги данного пункта, нами были изучены тела вращения и их свойства. Описали понятие тел вращения. Привели примеры. Проследили и пришли к выводу, что дети знакомятся с телами вращения уже в 1 классе начальной школы.