Тема 3.2. Понятие бесконечно малой величины.
Практических работ- нет
Тема 3.3. Дифференциал и его геометрический смысл.
Практическая работа № 17
«Дифференцирование сложной функции»
Цель работы:научиться дифференцировать.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- применять методы дифференциального и интегрального исчисления.
знать:
- основы дифференциального и интегрального исчисления.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
Краткие теоретические и учебно-методические материалы по теме практической работы
Понятие производной функции
Пусть функция ƒ (x) определена в некоторой окрестности точки x0. Производной функции ƒ (x) в точке x0называется отношение приращения функции ∆ƒ (x0) к приращению аргумента ∆x при ∆x → 0, если этот предел существует, и обозначается ƒ’(x0).
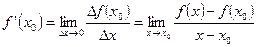 (1)
(1)
Производную функции y = ƒ (x), x є ( a;b ) в точке x обозначают ƒ’(x), y’(x), 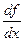 ,
, 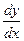 , причём все эти обозначения равноправны. Операция нахождения производной называется дифференцированием функции. Функция, имеющая производную в точке x0, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала (a;b), называется дифференцируемой на этом интервале; при этом производную ƒ’(x) можно рассматривать как функцию на (a ;b).
, причём все эти обозначения равноправны. Операция нахождения производной называется дифференцированием функции. Функция, имеющая производную в точке x0, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке интервала (a;b), называется дифференцируемой на этом интервале; при этом производную ƒ’(x) можно рассматривать как функцию на (a ;b).
Таблица производных элементарных функций
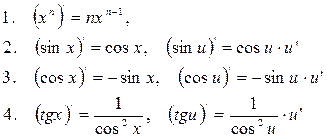
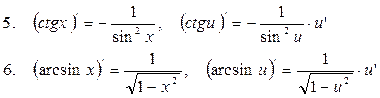
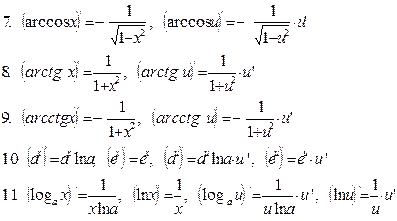
Правила дифференцирования
На практике применяют следующие правила дифференцирования
1. 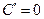
2. 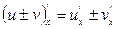 ,
,
3. 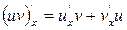 ,
, 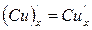 ;
;
4. 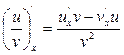 ,
,
где u и υ обозначают дифференцируемые функции переменной x, C - константа.
Дифференцирование сложной функции
Теорема.Пусть дана сложная функция 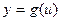 , где
, где 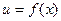 . Если функция
. Если функция 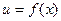 дифференцируема в некоторой точке х0, а функция
дифференцируема в некоторой точке х0, а функция 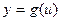 определена на множестве значений функции
определена на множестве значений функции 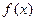 и дифференцируема в точке
и дифференцируема в точке 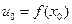 , то сложная функция
, то сложная функция 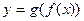 в данной точке х0 имеет производную, которая находится по формуле
в данной точке х0 имеет производную, которая находится по формуле
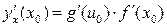 или
или 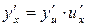
Пример по выполнению практической работы
Пример 1. Вычислить 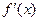 , если
, если 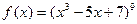 .
.
Решение:
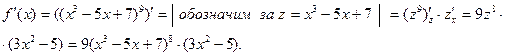
Пример 2. Вычислить 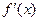 , если
, если 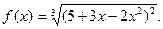
Решение:
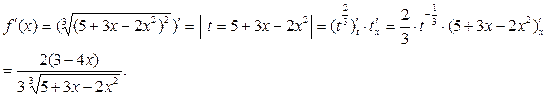
Пример 3. Вычислить 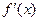 , если
, если 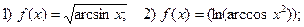
Решение:
1) 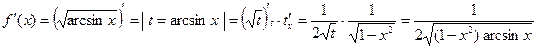 ;
;
2) данная функция является суперпозицией трех функций, поэтому имеем
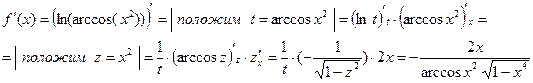
Задания для практического занятия:
Вариант 1
1. Вычислить производные следующих функций:
1) 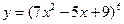 ; 2)
; 2) 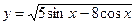 ; 3)
; 3) 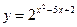 ;
;
4) 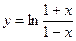 ; 5);
; 5); 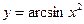 6)
6) 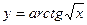 ;
;
2. Вычислить 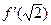 , если
, если 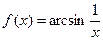 ;
;
3. Вычислить 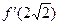 , если
, если 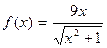 .
.
Вариант 2
1. Вычислить производные следующих функций:
1) 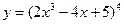 ; 2)
; 2) 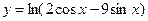 ; 3)
; 3) 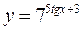 ;
;
4) 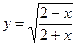 5)
5) 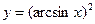 ; 6)
; 6) 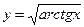 ;
;
2. Вычислить 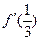 , если
, если 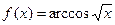 ;
;
3. Найти 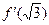 , если
, если 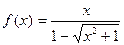 .
.
Вариант 3
1. Вычислить производные следующих функций:
1) 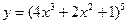 ; 2)
; 2) 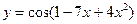 ; 3)
; 3) 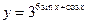 ;
;
4) 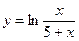 ; 5)
; 5) 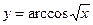 ; 6)
; 6) 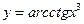 ;
;
2. Вычислить 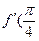 ), если
), если 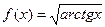 ;
;
3. Найти 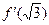 , если
, если 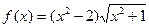 .
.
Вариант 4
1. Вычислить производные следующих функций:
1) 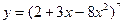 ; 2)
; 2) 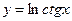 ; 3)
; 3) 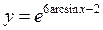 ;
;
4) 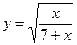 5)
5) 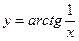 ; 6)
; 6) 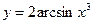 ;
;
2. Вычислить 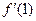 , если
, если 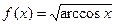 ;
;
3. Найти 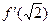 , если
, если 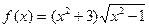 .
.
Контрольные вопросы
1. Что называется производной функции в точке?
2. Что такое дифференцирование?
3. Какая функция называется дифференцируемой в точке?
4. Перечислите табличные производные.
5. Какие правила дифференцирования вы знаете?
Практическая работа № 18
«Физические и геометрические приложения производной»
Цель работы:научиться применять физический и геометрический смысл
производной.
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
- применять методы дифференциального и интегрального исчисления.
знать:
- основы дифференциального и интегрального исчисления.
Оборудование: рабочая тетрадь, ручка, методические рекомендации по выполнению практической работы, справочная литература.
Методические указания по выполнению работы:
1. Ознакомиться с теоретическим материалом по практической работе.
2. Рассмотрите образцы решения задач по теме.
3.Выполнить предложенное задание согласно варианту по списку группы.
4.Изучить условие заданий для практической работы и выполнить её.
5. Ответить на контрольные вопросы даются письменно, после решения заданий в тетради для практических работ. Во время выполнения работы обучающийся может пользоваться своим конспектом, а также учебной литературой и справочным материалом.
5. Оформить отчет о работе. Сделайте вывод.
