Графическое определение передаточного отношения.

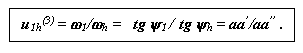
Двухрядный механизм с двумя внутренними зацеплениями.

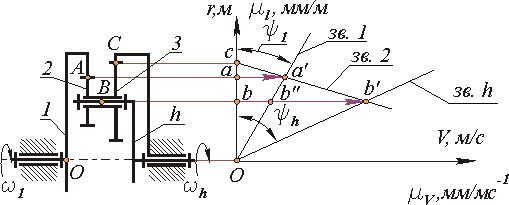
Рис.15.7

Аналитическое определение передаточного отношения.

В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:

z2 , который зацепляется с зубчатым венцом z1 звена 1

z3 , который зацепляется с внутренним зубчатым венцом z4 звена 3.

По формуле Виллиса отношение угловых скоростей звеньев для внутреннего зацепления колес z2 и z1 :

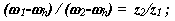
для внутреннего зацепления колес z4 и z3:

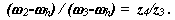
Перемножим, правые и левые части этих уравнений, и получим:

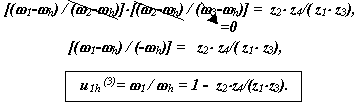
Графическое определение передаточного отношения.

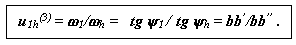
§ 5. Кинематическое исследование пространственных планетарных механизмов методом планов угловых скоростей.

Рассмотрим этот метод исследования на примере планетарного механизма конического дифференциала заднего моста автомобиля. На рис. 15.8 изображена схема механизма и планы угловых скоростей.

Рис.15.8

Планы угловых скоростей строятся в соответствии с векторными уравнениями:

w2=w1+w21; w4=w3+w43

w3=w2+w32; w5=w3+w53

Вектора относительных угловых скоростей направлены по осям мгновенного относительного вращения:

w21- по линии контакта начальных конусов звеньев 2 и 1;
w32- по оси шарнира С;
w43- по линии контакта начальных конусов звеньев 4 и 3;
w53 - по линии контакта начальных конусов звеньев 5 и 3.

Вектора абсолютных угловых скоростей направлены по осям кинематических пар, которые образуют звенья со стойкой:

w2 - по оси пары В ; w1 - по оси пары А ;
w4 - по оси пары Е ; w5 - по оси пары D .

Направление угловой скорости сателлита 3 определяется соотношением величин угловых скоростей w2 и w32 .

Рассмотрим три режима движения автомобиля:

• прямолинейное движение w4 = w5 (векторная диаграмма на рис.15.8a). В этом режиме движения корпус дифференциала 2 и полуоси 4 и 5 вращаются с одинаковыми угловыми скоростями w4 = w5 = w2 , а относительная угловая скорость сателлита w32=0.
• поворот автомобиля направо w4 < w5 (векторная диаграмма на рис.15.8б). При повороте направо угловые скорости полуосей не равны и связаны неравенством w4 < w5 , поэтому сателлит будет вращаться с такой угловой скоростью w32, которая обеспечивает постоянство угловой скорости корпуса дифференциала w2.
• буксование левого колеса w4 = 0 (векторная диаграмма на рис.15.8в). При буксовании левого колеса, правое колесо останавливается w4 = 0, а левое будет вращаться с угловой скоростью w5 = 2∙w2 .

Для того, чтобы в условиях низкого сцепления колес с грунтом, уменьшить опасность их пробуксовывания в дифференциалы автомобилей высокой проходимости включают элементы трения или блокировки.

Вопросы для самопроверки

- Какой зубчатый механизм называется сложным?

- Какой механизм называется планетарным?

- Как определить передаточное отношение одной из схем планетарного редуктора аналитическим способом ?

- Как используются графический и аналитический способы для определения угловых скоростей звеньев планетарных зубчатых механизмов?

- Как устанавливаются кинематические зависимости в планетарном зубчатом механизме с коническими колесами?

- Как используется графический способ для определения угловых скоростей звеньев дифференциалов?

- Какова цель применения метода обращения движения при кинематическом анализе планетарных механизмов?

- Что отличает передаточное отношение от передаточного числа?

- Как определяют передаточное отношение многоступенчатого рядового механизма? Какое участие в формуле передаточного отношения принимают числа зубьев связанных колес?

- Какие звенья планетарного механизма называют центральными?

- Что представляет собой «обращенный механизм»?

- Запишите формулы Виллиса: для дифференциальной ступени типа 2КН; для планетарной ступени типа 3К.

- Как вычисляют передаточное отношение комбинированного механизма с последовательным соединением ступеней?

- Опишите методику кинематического анализа замкнутого дифференциального механизма.

Вопросы для самопроверки

Задача 1

Сколько оборотов сделает колесо , когда водило H совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 2(см. рисунок к задаче 1)

Сколько оборотов сделает водило H, когда колесо совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 3(см. рисунок к задаче 1)

Определить величину передаточного отношения , если соотношение чисел зубьев колес .

Задача 4(см. рисунок к задаче 1)

Сколько оборотов сделает колесо относительно водила H, когда водило совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 5

Определить величину передаточного отношения , если соотношение чисел зубьев колес .

Задача 6(см. рисунок к задаче 5)

Сколько оборотов сделает водило H, когда колесо совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 7(см. рисунок к задаче 5)

Сколько оборотов сделает колесо , когда водило H совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 8(см. рисунок к задаче 5)

Сколько оборотов сделает колесо относительно водила H, когда последнее совершит один оборот; колесо неподвижно, соотношение чисел зубьев колес .

Задача 9

Найти угловую скорость сателлита , если =1 c^-1, =-1 c^-1. Соотношение чисел зубьев колес .

Задача 10

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 11(см. рисунок к задаче 10)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 12

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 13(см. рисунок к задаче 12)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 14

Для планетарной ступени комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 15(см. рисунок к задаче 3.14)

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес; рассчитать величину при =18; =36; =77; =22; =21; =75.

Задача 16(см. рисунок к задаче 14)

Для комбинированного редуктора установить условие, при выполнении которого его передаточное отношение .

Задача 17

Считая, что =3, найти частоту относительного вращения , если выходной вал B вращается с частотой =-10 об/мин.

Задача 18

Считая, что , найти частоту относительного вращения , если выходной вал вращается с частотой =-20 об/мин.

Задача 19

Формулу передаточного отношения редуктора 3К выразить через числа зубьев колес.

Задача 20(см. рисунок к задаче 19)

Для редуктора 3К написать условия соосности, соседства (в предположении, что ) и сборки, выразив их через числа зубьев колес.

Задача 21

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 22

Для непланетарной части комбинированного редуктора написать формулы для проверки условий соосности, соседства и сборки, выразив их через числа зубьев колес.

Задача 23

Для комбинированного редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес. Рассчитать величину при .

Задачи 24 – 26

Формулу передаточного отношения каждого из редукторов типа 4К выразить через числа зубьев колес.

Задача 27

Для планетарного двухступенчатого редуктора вывести формулу передаточного отношения , выразив его через числа зубьев колес.

Задача 28(см. рисунок к задаче 27)

Для планетарного двухступенчатого редуктора определить величину передаточного отношения при , .

Задача 29

Вал B редуктора вращается с частотой =100 об/мин, передаточное отношение редуктора =-25. Найти частоту вращения вала колеса относительно водила H, если соотношение чисел зубьев .

Задача 30

Вал B редуктора вращается с частотой =100 об/мин; найти частоту вращения колеса относительно вала водила H, если соотношение чисел зубьев .

Задача 31

Вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 32

Вал B редуктора вращается с частотой =100 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 33

Вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 25; найти частоту вращения колеса относительно вала A, если соотношение чисел зубьев .

Задача 34

Выходной вал B редуктора вращается с частотой =40 об/мин; найти частоту вращения колес и относительно вала водила, если соотношение чисел зубьев .

Задача 35

Выходной вал B редуктора вращается с частотой =40 об/мин, передаточное отношение редуктора = 31; найти частоту вращения колес и относительно входного вала, если соотношение чисел зубьев .

Задача 36

Передаточное отношение редуктора =-40, соотношение чисел зубьев , частота вращения входного вала =1400 об/мин; определить относительную частоту вращения .

Задача 37

Вал A редуктора вращается с частотой =1500 об/мин, передаточное отношение =40. Определить частоту вращения колеса относительно вала A, если =12.

Задача 38(см. рисунок к задаче 37)

Вал A редуктора вращается с частотой =1500 об/мин, передаточное отношение =40. Определить частоту вращения колеса относительно водила H, если .

Задача 39

Выходной вал B редуктора вращается с частотой =-40 об/мин, передаточное отношение редуктора =-35; найти частоту вращения водила H относительно вала A, если соотношение чисел зубьев .

Задача 40(см рисунок к задаче 39)

Входной вал A редуктора вращается с частотой =1400 об/мин, передаточное отношение редуктора =-35; найти частоту вращения водила H относительно вала A, если соотношение чисел зубьев .

Задача 41

Определить частоту вращения колеса относительно вала A, если и передаточное отношение редуктора =40. Выходной вал редуктора вращается с частотой =50 об/мин.

Задача 42

Определить частоту вращения колеса относительно вала водила , если передаточное отношение и частота вращения выходного вала =100 об/мин

Задача 43

Частота вращения вала A редуктора , передаточное отношение ; определить частоту относительного вращения , если .

Задача 44

Частота вращения вала A редуктора =1400 об/мин, передаточное отношение ; определить частоту вращения водила , если .

Задача 45

Передаточное отношение редуктора выразить через числа зубьев колес.

Задача 46(см. рисунок к задаче 44)

Рассчитать передаточное отношение редуктора при следующих соотношениях чисел зубьев: ; .

Задача 47

Водило OAB планетарного механизма вращается с угловой скоростью =15 рад/с, колесо неподвижно. Определить угловые скорости сателлитов и , если числа зубьев колес =30, =20.

Задача 48

Рассчитать передаточное отношение редуктора, если числа зубьев колес равны: =33; =36.

Задача 49(см. рисунок к задаче 47)

Подобрать числа зубьев колес и редуктора, обеспечивающих получение передаточного отношения , если разность .