Расчет и конструирование узлов арки.
Расчет узлов арок производится на максимальные действующие в них продольные N и поперечные Q силы.
Опорный узел клеедеревянной арки без затяжки проверяется по прочности древесины при смятии по формуле:
s=N/Aсм≤Rсм.
В опорном узле сегментной или стрельчатой арки торец полуарки перпендикулярен ее оси, продольная сила N действует вдоль волокон древесины при угле смятия a=0, и расчетное сопротивление смятию является максимальным, равным расчетному сопротивлению сжатию Rс. В опорном узле треугольной арки торец полуарки обычно перпендикулярен продольной и поперечной силе, и сминающая сила
Nсм = 
Эта продольная сила действует под углом к волокнам древесины, определяемым из выражения tga=Q/N и расчетное сопротивление смятию Rсмa соответственно несколько ниже.
Число болтов крепления конца сегментной и стрельчатой арок к боковым фасонкам башмака определяется по величине попе- речной силы Q, как двухсрезных, работающих симметрично при стальных накладках под углом a =90° к волокнам древесины. В опорном узле треугольной арки, где равнодействующая сил N и Q действует перпендикулярно торцу полуарки, сдвигающая сила отсутствует, и болты крепления являются не расчетными, а конструктивными.
Опорный лист башмака работает на изгиб как балка на упругом основании. Максимальный изгибающий момент в его сечении при расчетной ширине b = 1 см определяется по приближенной формуле:
M= (q1l12-q2l22)/8,
где q1 и q2 равны давлению торца полуарки и реактивному давлению фундамента, а l1 и l2 равны соответственно длине листа и ширине сечения арки.
Требуемая толщина опорного листа d определяется из выражения
dтр = 
Анкерные болты рассчитываются на срез и смятие при действии поперечных сил по нормам проектирования стальных конструкций. Поверхность опор рассчитывается на смятие от действия продольных сил N.
При расчете конькового узла сегментной клеедеревянной арки со стальными узловыми креплениями проверяется прочность лобовых упоров торцов полуарок в упорные листы креплений на смятие продольными силами, действующими вдоль волокон древесины. Число двухсрезных симметрично работающих болтов, соединяющих концы полуарок с фасонками креплений, определяется по величине поперечной силы Q, действующей в узле, с учетом того, что эта сила давит на болты под углом смятия a=90° к волокнам древесины, поэтому при определении несущей способности болтов надо вводить коэффициент Ka. Монтажные болты, соединяющие упорные листы, рассчитывают на действие поперечной силы. Стальные листы крепления не требуют расчета, так как обычно работают со значительными запасами прочности.
Расчет коньковых узлов треугольных и стрельчатых клеедеревянных арок производится аналогично с учетом того, что продольная и поперечная силы действуют здесь под углами к волокнам древесины, равными a и 90-a, где a— угол наклона касательной к оси полуарки в этом узле.
Расчет коньковых узлов клеедеревянных и брусчатых малопролетных арок с накладками из толстых досок или клеедеревянными и с болтовыми креплениями производится на смятие торцов полуарок продольными силами N. Требуемое число соединительных болтов определяется при действии поперечной силы Q. При этом каждая половина накладки условно считается консольной балкой пролетом l, равным расстоянию между рядами болтов, и консолью a, равной расстоянию крайнего ряда болтов от оси узла, где действует поперечная сила Q. При этом в ближайшем к оси узла ряду болтов возникает усилие R1 = Q(l + а)/l, а в дальнем ряду — R2 = Qa/l. По этим усилиям определяются требуемые количества болтов с учетом того, что они работают под значительными углами к волокнам древесины как двухсрезные и симметричные. В ближайшем к оси узла ряду ставятся обычно два болта, а в более дальнем — один болт. Сами накладки обычно работают на изгиб с избыточным запасом прочности.
Приложение 1.
Пример расчета трехшарнирной клееной арки кругового очертания.
Конструирование арок.
Конструктивное решение: трехшарнирная клеедеревянная арка кругового очертания постоянного прямоугольного сечения без затяжки. Пролет - 15м. Высота - 4.85м. Материал - древесина 2 сорта. Шаг арок – 3м. Район строительства - Тюмень.
Определение геометрических размеров (рис. 1).
Начало прямоугольных координат принимается в центре левого опорного узла арки.
Определяем радиус арки:
r = (l2+4f2)/(8f)=(152+4*4.852)/(8*4.85)=8.22 м.
Длина дуги арки:
S= 
Центральный угол дуги полуарки:
sinj=l/(2r)=15/(2*8.22)=0.9, этому соответствует j=660; cosj=0.41;

Рис. 1. К расчету круговой арки.
Сбор нагрузок. 
Собственный вес арки:
 =
=  =11.27 кг/м2,
=11.27 кг/м2,
где gн – нормативная нагрузка от покрытия, кровли и утеплителя;
рн – нормативная снеговая нагрузка;
ксв – коэффициент собственного веса (для арок принимается равным 4-5)
Табличный сбор нагрузок без учета криволинейности элемента.
Таблица 1
| Наименование нагрузок | Нормативная, кг/м2 | Коэффициент надежности по нагрузке gf | Расчетная, кг/м2 |
| Кровля (металлочерепица) | 1,2 | 5,25 | |
| Покрытие (рабочий досчатый настил t=35мм.) | 1,1 | 16,5 | |
| Покрытие (досчатый настил t=25мм.) | 10,5 | 1,1 | 11,55 |
| Утеплитель δ=100мм, 2 слоя пароизоляции | 1,2 | ||
| Арка | 11,27 | 1,1 | 12,40 |
| Итого | q 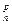 =61,77 =61,77 | q 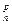 =69,70 =69,70 | |
| Снег по [2] п. 5.2, табл. 4 | |||
| Всего | qн =187,77 | qр =249,70 |
Расчетная нагрузка с учетом разницы между длиной дуги арки и ее проекцией (S/l).
Постоянная  =(5.25+16.50+11.55+24)*S/l=57.30*18.7/15=71.43 кг/м2
=(5.25+16.50+11.55+24)*S/l=57.30*18.7/15=71.43 кг/м2
Временная р=с*р*m2=0,4*180*2,25=162 кг/м2,
где с=l/(8f) – коэффициент снегозадержания для криволинейных покрытий.
Расчетная нагрузка на 1 п.м. арки:
Постоянная g=(71.43+12.40)*3.00=251.49 кг/м.
Временная р=162*3.00=486.00 кг/м.
Ветровая нагрузка не учитывается, т.к. разгружает конструкцию.
Вычисления усилий приводятся только в основных расчетных сечениях. Полупролет арки делитсяна четыре равных части, образующих пять сечений от x=0 до x=7,5 м. Согласно прил.3 п.2 [2] определяем координаты (х,у) дополнительного сечения арки, соответствующее φ=50  . Координаты сечений, углы наклона касательных к оси полуарки в этих сечениях определяются по формулам:
. Координаты сечений, углы наклона касательных к оси полуарки в этих сечениях определяются по формулам:
у= 
где Д=r-f=8.22-4.85=3.37м.
j=arcsin((l/2-x)/r).
Геометрические величины оси левой полуарки.
Таблица 2
| Координаты | 0’ | |||||
| Х,м | 1,203 | 1,875 | 3,75 | 5,625 | 7,5 | |
| У,м | 1,914 | 2,624 | 3,945 | 4,633 | 4,85 | |
φ  |
Статический расчет.
Сочетания нагрузок (рис.1 прил.2 методических указаний):
1. Постоянная + снег по всему пролету (по треугольно распределенной форме)
(см рис1а.)
2. Постоянная + снег слева (по треугольно распределенной форме) (см рис1б)
3. Постоянная + снег справа (по треугольно распределенной форме) (см рис1в)
а) от равномерно распределенной нагрузки по всему пролету (постоянной):
Определяем опорные реакции:
VА=VВ=ql/2=251.49*15/2=1886.18 кг.
Н=ql2/8f=251.49*152/8*4.85=1458.38 кг.
Определяем усилия:
Мх=VА=Бx-qx2/2-Hy;
Qx=(VA=Б-qx)cosj-Hsinj; 
Nx=(VA=Б-qx)sinj+Hcosj;
б) От распределенной по треугольнику нагрузке на полупролете слева р=486.00 кг/м.
VА=5рl’/24=5*486.00*12.594/24=1275.14 кг.
VВ=рl’/24=486.00*12.594/24=255.03 кг.
Н=l’2*p/(48f)=12.2942*486.00/(48*4.85)=331.12 кг.,
где l’=l-2х=15.000-2*1.203=12.594 м.
На участке 0≤х≥l/2: На участке l/2≤х≥l:
Мх= VАx-px2/2+px3/(3l’)-Hy; Мх= VБ (l’-x) -Hy;
Qx=(VA-px+px2/l’)cosj-Hsinj; Qx=-VБcosj+Hsinj
Nx=(VA-px+px2/l’)sinj+Hcosj; Nx=-VБsinj-Hcosj;
Примечание:
1) при определении усилий Мх Qx Nx значения координаты (y) в сечениях принимаем согласно табл.2, значения координаты х =хn -1.203,
где хn –координата х в n сечении.
2) при определении усилий в опорных шарнирах принимаем х=1.203 ; р=0
в) От распределенной по треугольнику нагрузке на полупролете справа р=486.00 кг/м.
Расчет выполняется аналогично п.б), при этом
VА=рl’/24=486.00*12.594/24=255.03 кг.
Vв=5рl’/24=5*486.00*12.594/24=1275.14 кг.
Н=l’2*p/(48f)=12.2942*486.00/(48*4.85)=331.12 кг.
г) Усилия от распределенной по треугольнику нагрузке на всем пролете определяются путем суммирования усилий от снеговых нагрузок на левом и правом полупролетах арки.
Вертикальная опорная реакция арки V определяется из условия равенства нулю изгибающего момента в противоположном опорном шарнире. Горизонтальная опорная реакция Н, численно равная распору арки без затяжки, определяется из условия равенства нулю изгибающего момента в коньковом шарнире.
Усилия в арке определяются методами строительной механики в основных расчетных сечениях. Промежуточные вычисления опускаются.
Результаты их сводятся в таблицу 3.
Эпюры усилий от сочетания нагрузок М, Q, N приведены в прил. 2 рис.2. методических указаний.
Усилия в сечениях арки
Таблица 3
| Сечение | Усилия | ||||||||||
| от постоян-ной нагрузки | От снеговой по треугольно распределенной форме. треугольной распределенной | Расчетные | |||||||||
| на левом полупролете | на правом полупролете | на всем пролете | |||||||||
| М (кг м) | |||||||||||
| 0’ | -704.24 | -633.76 | -633.76 | -1267.52 | -1337.96 | -1971.76 | |||||
| -732.27 | -117.80 | -697.48 | -815.28 | -850.07 | -1547.55 | ||||||
| -448.42 | 577.66 | -656.71 | -79.05 | 129.24 | -527.47 | ||||||
| -125.56 | 465.21 | -406.34 | 58.87 | 339.65 | -66.69 | ||||||
| -125.56 | -406.34 | 465.21 | 58.87 | -531.90 | -66.69 | ||||||
| -448.42 | -656.71 | 577.66 | -79.05 | -1105.13 | -527.47 | ||||||
| -732.27 | -697.48 | -117.80 | -815.28 | -1429.75 | -1547.55 | ||||||
| 8’ | -704.24 | -633.76 | -633.76 | -1267.52 | -1337.96 | -1971.76 | |||||
| Q (кг) | |||||||||||
| -565.12 | 216.15 | 198.76 | 414.91 | -348.97 | -150.21 | ||||||
| 0’ | -99.24 | 565.99 | 89.72 | 655.71 | 466.75 | 556.47 | |||||
| 39.99 | 480.65 | 39.31 | 519.96 | 520.64 | 559.95 | ||||||
| 178.21 | 105.96 | -76.91 | 29.05 | 284.17 | 207.26 | ||||||
| 131.40 | -190.79 | -174.01 | -364.80 | -59.39 | -233.40 | ||||||
| ±255.03 | ±255.03 | ±255.03 | ±255.03 | ±255.03 | |||||||
| 131.40 | -174.01 | -190.79 | -364.80 | -42.61 | -233.40 | ||||||
| 178.21 | -76.91 | 105.96 | 29.05 | 101.30 | 207.26 | ||||||
| 39.99 | 39.31 | 480.65 | 519.96 | 79.30 | 559.95 | ||||||
| 8’ | -99.24 | 89.72 | 565.99 | 655.71 | -9.52 | 556.47 | |||||
| -565.12 | 198.76 | 216.15 | 414.91 | -366.36 | -150.21 | ||||||
| N (кг) | |||||||||||
| 2316.29 | 1299.58 | -367.66 | 931.92 | 3615.87 | 3248.21 | ||||||
| 0’ | 2150.56 | 1189.65 | -408.20 | 781.45 | 3340.21 | 2932.01 | |||||
| 2031.37 | 900.96 | -416.10 | 484.86 | 2932.33 | 2516.23 | ||||||
| 1727.58 | 425.62 | -410.81 | 14.81 | 2153.20 | 1742.39 | ||||||
| 1527.08 | 295.78 | -380.00 | -84.22 | 1822.86 | 1442.86 | ||||||
| 1458.38 | ±331.12 | ±331.12 | ±331.12 | 1127.26 | 1127.26 | ||||||
| 1527.08 | -380.00 | 295.78 | -84.22 | 1147.08 | 1442.86 | ||||||
| 1727.58 | -410.81 | 425.62 | 14.81 | 1316.77 | 1742.39 | ||||||
| 2031.37 | -416.10 | 900.96 | 484.86 | 1615.27 | 2516.23 | ||||||
| 8’ | 2150.56 | -408.20 | 1189.65 | 781.45 | 1742.36 | 2932.01 | |||||
| 2316.29 | -367.66 | 1299.58 | 931.92 | 1948.63 | 3248.21 | ||||||
Подбор сечения арок.
Подбор сечения производим по максимальным усилиям:
Мmax=-1971.76 кг м., N соотв.=2932.01кг.
Оптимальная высота поперечного сечения арки находится:
hопт=(1/30-1/40)l=(0.5-0.375) м.
Требуемая высота сечения арки находится из условия устойчивости
в плоскости кривизны:
l=  ,
,
где l=120 – предельная гибкость, принимаемая по[1]табл.14;
l0=0,58S - расчетная длина элемента;
i =0.29h - радиус сечения элемента.
Отсюда hтр = 
Ширину сечения арки принимаем b=0.1м. по сортаменту пиломатериалов, рекомендуемых для клееных конструкций. [5] прил. 1
Толщину досок принимаем, а=2.5 см, а после острожки с двух сторон, а=2.1 см.
Поперечное сечение принимаем прямоугольным , постоянной высоты и ширины. Компонуем из 17 досок сечением 10х2.1 см, тогда высота сечения h=17*2.1=35.7=36 см.
Принятое сечение b x h=10x36 см.
