Конфигурация силовых линий основного типа поля

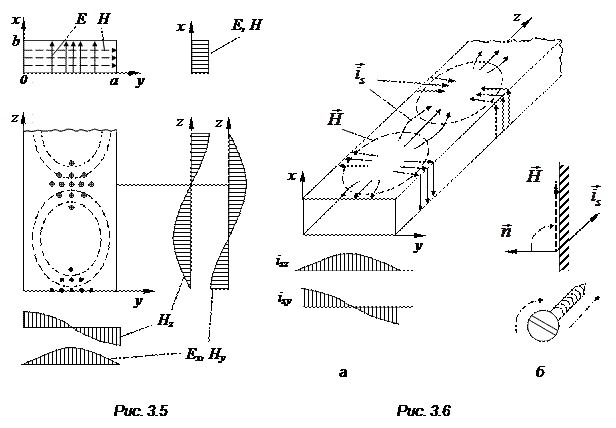
В формулах (3.27), (3.28) индекс «–» в показательной функции соответствует волне, бегущей в направлении +z, а индекс «+» – волне обратного направления. На рис. 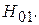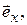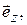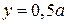3.5 изображен мгновенный «снимок» силовых линий электрического и магнитного полей волны Электрическое поле линейно поляризовано вдоль орта магнитное имеет эллиптическую поляризацию, которая у боковых стенок вырождается в линейную по орту а при – в линейную по орту 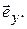На верхней и нижней стенках волновода 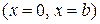имеются поверхностные заряды, плотность которых 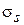пропорциональна густоте силовых линий вектора 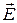в данной точке тонки. По стенкам текут поверхностные токи. Связь между вектором 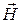и вектором плотности поверхностного тока 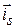определяется известным граничным условием на поверхности металла:

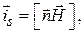(3.29)

где 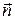– орт, направленный перпендикулярно к поверхности металла (рис. 3.6, б). На рис. 3.6, а изображена мгновенная картина линий вектора плотности поверхностного тока 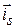, построенная согласно формуле (3.29). Направление линий тока определяется правилом «правого винта» (рис. 3.6, б).

Перенос мощности по волноводу

Использование нормированных собственных функций (3.27), (3.28) позволяет представить реальное поле в волноводе основного типа 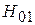в следующем виде:

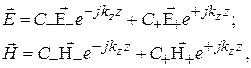(3.30)

где 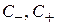– безразмерные комплексные амплитуды, соответственно падающей «–» и обратной «+» волн; 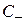определяется мощностью генератора, а 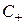еще зависит и от согласования волновода с нагрузкой. Средняя за период колебаний мощность, переносимая по волноводу падающей (прямой) и отраженной (обратной) волнами (3.30) определится очевидным образом:

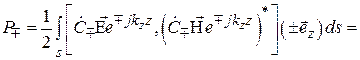
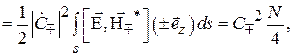(3.31)

где 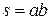– площадь поперечного сечения волновода. Таким образом, уровень переносимой мощности по волноводу (3.30) пропорционален квадратам модулей безразмерных амплитуд волн 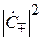, а норма N играет роль параметра, определяющего размерность мощности в ваттах (3.31).

Режим бегущей волны

В лабораторной работе исследуется волновой режим в волноводе, связывающем генератор и нагрузку. Рабочая частота выбирается так, чтобы в нем могла распространяться лишь основная мода 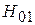(одномодовый режим). Если на конце волновода включена, согласованная Нагрузка, то в волноводе присутствует лишь падающая волна 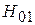с некоторой амплитудой С_–; ее поле можно представить в виде

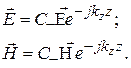(3.32)

Модули всех компонент электрического и магнитного полей (3.32) не зависят от z, а их фазы изменяются по линейному закону. Свойствами согласованной нагрузки могут обладать самые различные волновые двухполюсники. В практике измерений на СВЧ согласованные нагрузки обычно представляют собой отрезки волновода с клинообразной поглощающей вставкой из ферроэпоксида.

Режим смешанных волн

В общем случае нагрузка, включенная на конце волноводной линии в той или иной мере отражает, так что в волноводе одновременно присутствуют падающая и отраженная волны с амплитудам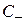и и 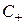(режим смешанных волн). Электрическое и магнитное поля этих волн могут быть записаны в виде формул (3.30). Для удобства, анализа явлений в волноводе целесообразно ввести (аналогично тому, как это сделано в длинной линии, см. 2) обратную продольную координату 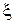, отсчитываемую от нагрузки в сторону генератора, выразив координату z следующим образом:

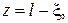(3.33)

где 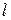– длина волновода от генератора до нагрузки.

Целесообразно также, как это сделано в длинной линии (см. (2.26)), ввести понятие коэффициента отражения от нагрузки:

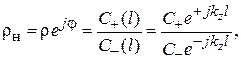(3.34)

где 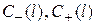– амплитуды падающей и отраженной волн на нагрузке (на конце волновода). Подстановка формул (3.33) и (3.34) в формулы (3.30) позволяет электрическое и магнитное поля представить в следующем виде:

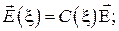(3.35)

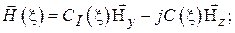(3.36)

где

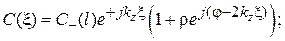(3.37)

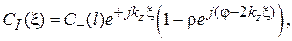(3.38)

где 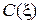– комплексная амплитуда напряженности электрического поля волновода; 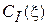– комплексная амплитуда поперечной составляющей вектора напряженности магнитного поля волновода.

Из (3.35)–(3.38) видно, что продольная составляющая вектора напряженности магнитного поля распределена так, как вектор напряженности электрического поля. Сравнивая (3.35) и (3.36) с (2.24) и (2.25), можно обнаружить прямую аналогию в описании волновых явлений волновода и длинной линии.

Функция продольного распределения электрического поля 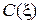аналогична распределению напряжения 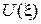в длинной линии. Распределение поперечной составляющей магнитного поля в волноводе (функция 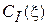) аналогична распределению тока 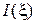в длинной линии. В силу этой аналогии функци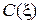и и 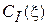подчиняются тем же закономерностям, которые известны для функци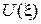й и 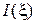соответственно. Все, что сказано о распределении модуле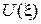й и 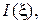полностью относится к функциям 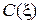и 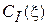(наличие максимумов и минимумов, их величины, понятия КБВ и КСВ, их связь с модулем коэффициента отражения, режимы бегущей, стоячей и смешанных волн, понятия условных концов и т. д.). При переходе от длинных линий к волноводам необходимо произвести следующие замены в соответствующих формулах, рисунках, векторных диаграммах, функциях продольного распределения амплитуд и т. п.:

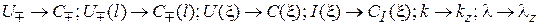
и т. д. Коэффициент отражения в волноводе обладает теми же свойствами, что и коэффициент отражения в длинной линии. Изложенная в 2 методика измерений длины волны, коэффициентов отражения и другое полностью распространяется на волноводы.

Поэтому при подготовке к выполнению данной работы следует подробно ознакомиться с 2. Выражения из 2 перепишутся для волноводов следующим образом:

1) распределение нормированного значения модуля амплитуды электрического поля:

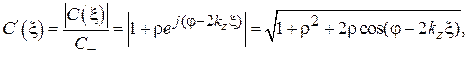(3.39)

2) распределение нормированного значения модуля амплитуды поперечной составляющей магнитного поля :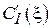

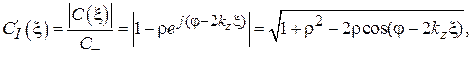(3.40)

3) КБВ, КСВ и модуль коэффициента отражения :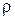

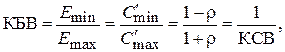(3.41)

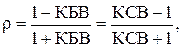(3.42)

4) расстояние между соседними условными концами волновода:

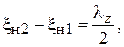(3.43)

5) определение фазы коэффициента отражения от нагрузки 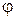(см. (1.23)):

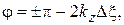(3.44)

где 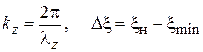, 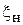– положение условного конца; 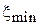– положение минимума электрического поля при установке на конце волновода нагрузки.

Формулы (3.39.) – (3.42), (3.44) идентичны формулам (2.32), (2.33). (2.36), (2.37), (1.23).