Конфигурация силовых линий полей в длинных линиях

На рис. 2.1, а изображены силовые линии векторов и плоской
Т-волны, распространяющейся вдоль оси z.

Если перпендикулярно линиям электрического поля поставить две параллельные идеально проводящие плоскости (рис. 2.1), то поле плоской
Т-волны (2.1) останется неизменным (согласно известному граничному условию на поверхности идеального металла равенства нулю касательной составляющей электрического поля: ). Поэтому между параллельными идеально проводящими плоскостями могут распространяться плоские
Т-волны. Непрерывной деформацией этих плоскостей в цилиндрические поверхности и поля между ними можно получить электромагнитное поле волны в коаксиальной и двухпроводной линиях (рис. 2.1, в, г). На рис. 2.1, д, е изображены симметричная и несимметричная полосковые линии и поля в них.

Из этих рассуждений следует, что возможно существование Т-волны в длинных линиях. Определим условия существования таких волн. Из структуры поля между двумя параллельными плоскостями однозначно следует, что поверхностный электрический ток на пластинах имеет только продольную составляющую:

(2.2)

2.3. Вектор напряженности магнитного поля в Т-волне

Граничное условие на идеальном металле однозначно связывает вектор напряженности магнитного поля и вектор плотности поверхностного тока :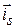

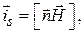(2.3)

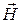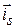где n – орт, нормальный к поверхности металла. Условие (2.3) означает, что векторы и перпендикулярны. Из (2.2) и (2.3) следует, что в длинных линиях вектор 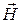имеет только поперечную составляющую:

(2.4)

Так как (в среде отсутствует внутренняя и внешняя намагниченности, магнитная проницаемость среды μ не зависит от координат), то силовые линии представляют собой замкнутые кольца в поперечном сечении линии. Кольца вектора охватывают токи проводников по правилу правого винта: если правый винт вращать по направлению силовых линий , то поступательное движение винта укажет направление тока. Таким образом, продольный ток (2.19) однозначно определяет поперечное магнитное поле (2.4).

2.4. Вектор напряженности электрического поля 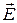в линии

Для определения вектора напряженности электрического поля в линии его можно представить через скалярный ψ и векторный потенциалы:

(2.5)

Использование условия калибровки Лоренца для потенциалов

(2.6)

позволяет однородные уравнения Максвелла преобразовать к однородному волновому уравнению для потенциала:

(2.7)

Потенциалы представляются в виде произведения двух функций: функции поперечных координат и экспоненциального множителя описывающего распространение волны вдоль оси линии z:

(2.8)

где – функции поперечных координат; 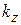– продольное волновое число, пусть пока неизвестное. Подставляя (2.8) в (2.6), а затем (2.6.) и (2.8) в (2.5) и (2.7), можно после преобразований получить волновое уравнение для функции ψ:

(2.9)

и формулу, для определения напряженности электрического поля:

(2.10)

где – поперечное волновое число:

(2.11)

Из формул (2.9)–(2.11) следует, что, если продольное волновое число 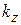отлично от , т. е. то в поле 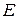обязательно имеется продольная составляющая. Это соответствует случаю 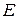– волн в длинной линии со всеми вытекающими отсюда свойствами волн, как для волноводов.

2.5. Т-волны

Однако формулы (2.9)–(2.11) позволяют обнаружить и другой класс волн. Если положить (см. (2.11)) то из уравнений (2.10), (2.9) следует:

(2.12)

(2.13)

где – векторная функция поперечных координат электрического поля. Подстановка (2.13) в уравнение Максвелла позволяет найти вектор напряженности магнитного поля:

(2.14)

где – векторная функция поперечных координат магнитного поля.

Поле, представленное формулами (2.13), (2.14), точно соответствует
Т-волнам:

и – синфазны;

(2.15)

– фазовая скорость Т-волны равна скорости света. Скалярный потенциал поперечном сечении линии удовлетворяет уравнению Лапласа (2.12), типичному для электростатических задач. Вектор напряженности электрического поля в поперечном сечении определяется как градиент потенциала , т. е. в поперечном сечении электрическое поле градиентно. Таким образом, функция в (2.13) является по структуре статическим полем, которое возникло бы между проводниками линии при подаче на них неизменной во времени разности потенциалов. В связи с этим говорят, что электрическое поле Т-волны имеет «электростатический характер». Такое поле в линии (2.13)–(2.15), поле Т-волны может быть названо квазистатическим. Формулы (2.13) и (2.14) для электромагнитного поля Т-волны получены с точностью до постоянных множителей – амплитуд, определяемых мощностью генератора 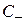и отражением от нагрузки линии 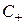. С учетом этих амплитуд поле в линии будет иметь вид

(2.16)

(2.17)

Структура электромагнитных полей для Т-волн (2.16), (2.17) в различных линиях получается различной в зависимости от конкретной геометрии поперечного сечения линии, конфигурации проводников, их размеров, относительного положения.