Вывод формул для нахождения коэффициентов.

Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 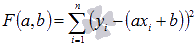по переменным а и b, приравниваем эти производные к нулю.

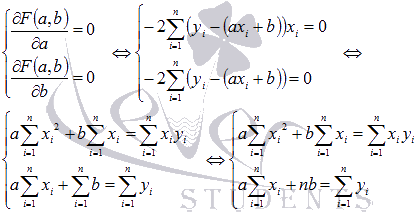
Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).

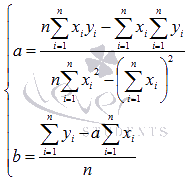
При данных а и b функция 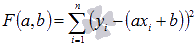принимает наименьшее значение. Доказательство этого факта приведено ниже по тексту в конце страницы .

Вот и весь метод наименьших квадратов. Формула для нахождения параметра aсодержит суммы 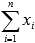, , 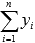, 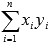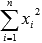и параметр n - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.

Пришло время вспомнить про исходый пример.

Решение.

В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.

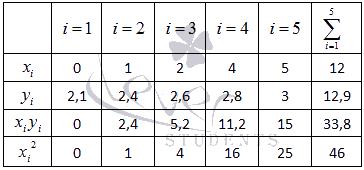
Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i .

Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i .

Значения последнего столбца таблицы – это суммы значений по строкам.

Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы:

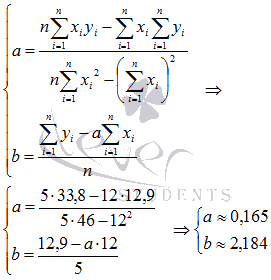
Следовательно, y = 0.165x+2.184 - искомая аппроксимирующая прямая.

Осталось выяснить какая из линий y = 0.165x+2.184 или 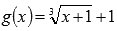лучше аппроксимирует исходные данные, то есть произвести оценку методом наименьших квадратов.

Оценка погрешности метода наименьших квадратов.

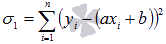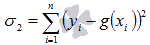Для этого требуется вычислить суммы квадратов отклонений исходных данных от этих линий и , меньшее значение соответствует линии, которая лучше в смысле метода наименьших квадратов аппроксимирует исходные данные.

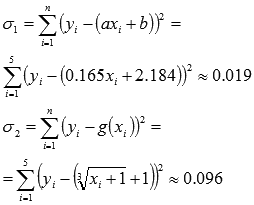
Так как 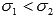, то прямая y = 0.165x+2.184 лучше приближает исходные данные.

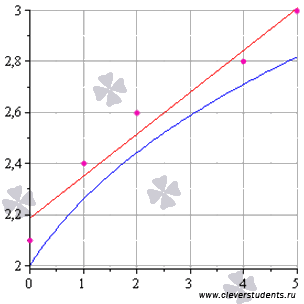
Графическая иллюстрация метода наименьших квадратов (мнк).

На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 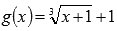, розовые точки – это исходные данные.

Для чего это нужно, к чему все эти аппроксимации?

Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.

Доказательство.

Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 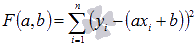была положительно определенной. Покажем это.

Дифференциал второго порядка имеет вид:

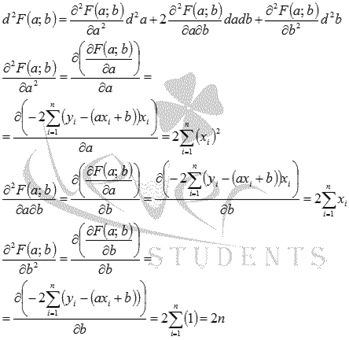
То есть

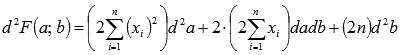
Следовательно, матрица квадратичной формы имеет вид

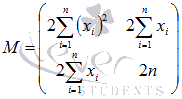
причем значения элементов не зависят от а и b .

Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.

Угловой минор первого порядка 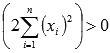. Неравенство строгое, так как точки несовпадающие. В дальнейшем это будем подразумевать.

Угловой минор второго порядка

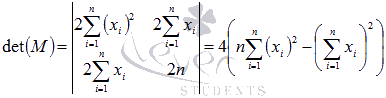
Докажем, что 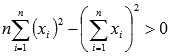методом математической индукции.

1. Проверим справедливость неравенства для любого значения n, например для n=2.

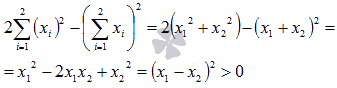
Получили верное неравенство для любых несовпадающих значени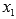й и .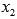

2. Предполагаем, что неравенство верное для n.

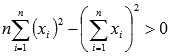- верное.

3. Докажем, что неравенство верное для n+1.

То есть, нужно доказать, что 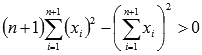исходя из предположения что 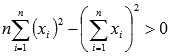- верное.

Поехали.

Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.

Вывод: найденные значения а и b соответствуют наименьшему значению функции 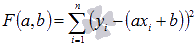, следовательно, являются искомыми параметрами для метода наименьших квадратов.

http://www.ekonomika-st.ru/drugie/metodi/metodi-prognoz-1-5.html

Разработка прогноза с помощью метода наименьших квадратов. Пример решения задачи

Экстраполяция - это метод научного исследования, который основан на распространении прошлых и настоящих тенденций, закономерностей, связей на будущее развитие объекта прогнозирования. К методам экстраполяции относятся метод скользящей средней, метод экспоненциального сглаживания, метод наименьших квадратов.

Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Расчетные величины находятся по подобранному уравнению – уравнению регрессии. Чем меньше расстояние между фактическими значениями и расчетными, тем более точен прогноз, построенный на основе уравнения регрессии.

Теоретический анализ сущности изучаемого явления, изменение которого отображается временным рядом, служит основой для выбора кривой. Иногда принимаются во внимание соображения о характере роста уровней ряда. Так, если рост выпуска продукции ожидается в арифметической прогрессии, то сглаживание производится по прямой. Если же оказывается, что рост идет в геометрической прогрессии, то сглаживание надо производить по показательной функции.

Рабочая формула метода наименьших квадратов: У t+1 = а*Х + b, где t + 1 – прогнозный период; Уt+1 – прогнозируемый показатель; a и b - коэффициенты; Х - условное обозначение времени.

Расчет коэффициентов a и b осуществляется по следующим формулам:

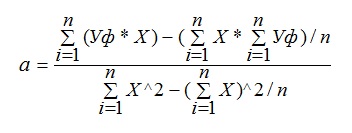
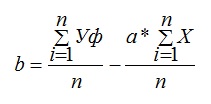
где, Уф – фактические значения ряда динамики; n – число уровней временного ряда;

Сглаживание временных рядов методом наименьших квадратов служит для отражения закономерности развития изучаемого явления. В аналитическом выражении тренда время рассматривается как независимая переменная, а уровни ряда выступают как функция этой независимой переменной.

Развитие явления зависит не от того, сколько лет прошло с отправного момента, а от того, какие факторы влияли на его развитие, в каком направлении и с какой интенсивностью. Отсюда ясно, что развитие явления во времени выступает как результат действия этих факторов.

Правильно установить тип кривой, тип аналитической зависимости от времени – одна из самых сложных задач предпрогнозного анализа.

Подбор вида функции, описывающей тренд, параметры которой определяются методом наименьших квадратов, производится в большинстве случаев эмпирически, путем построения ряда функций и сравнения их между собой по величине среднеквадратической ошибки, вычисляемой по формуле:

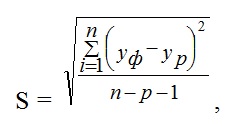
где Уф – фактические значения ряда динамики; Ур – расчетные (сглаженные) значения ряда динамики; n – число уровней временного ряда; р – число параметров, определяемых в формулах, описывающих тренд (тенденцию развития).

Недостатки метода наименьших квадратов:

· при попытке описать изучаемое экономическое явление с помощью математического уравнения, прогноз будет точен для небольшого периода времени и уравнение регрессии следует пересчитывать по мере поступления новой информации;

· сложность подбора уравнения регрессии, которая разрешима при использовании типовых компьютерных программ.

Пример применения метода наименьших квадратов для разработки прогноза

Задача. Имеются данные, характеризующие уровень безработицы в регионе, %

Январь	Февраль	Март	Апрель	Май	Июнь	Июль	Август	Сентябрь	Октябрь
2,99	2,66	2,63	2,56	2,40	2,22	1,97	1,72	1,56	1,42

· Постройте прогноз уровня безработицы в регионе на ноябрь, декабрь, январь месяцы, используя методы: скользящей средней, экспоненциального сглаживания, наименьших квадратов.

· Рассчитайте ошибки полученных прогнозов при использовании каждого метода.

· Сравните полученные результаты, сделайте выводы.