Работы, выполненные не по шифру, к проверке и защите не принимаются.

Решение задач необходимо сопровождать краткими пояснениями, всеми необходимыми расчетами и четкими схемами с указанием в необходимых случаях масштабов длин и сил.

Схемы заданий и методические указания

По их выполнению

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1

РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СИСТЕМ

НА ДЕЙСТВИЕ НЕПОДВИЖНОЙ НАГРУЗКИ

Задача 1.1. Расчет шарнирно-консольной балки

Литература: [1, с. 60–67], [3, c. 54–59], [4, c. 22–26],

[5, c. 98–101], [6, c. 12–21].

Исходные данные к задаче определяются по табл. 1.1 и схемам, представленным на рис. 1.1 и 1.2.

Последовательность расчета

1.1.1. Изобразить в масштабе схему балки с указанием размеров и действующих нагрузок.

1.1.2. Произвести анализ геометрической неизменяемости заданной схемы балки. Для этого использовать выражение, представляющее собой необходимое условие геометрической неизменяемости шарнирно-консольной балки Ш = С – 3, где Ш – число промежуточных шарниров; С – количество опорных связей, и выполнить анализ структуры взаимодействия отдельных дисков, построив поэтажную схему.

1.1.3. Показать схему взаимодействия отдельных дисков, расчленив заданную схему на главные и второстепенные балки, и определить реакции в связях от заданной нагрузки, составляя уравнения равновесия для каждого диска. Порядок рассмотрения дисков – сверху вниз по поэтажной схеме.

1.1.4. Показать схему взаимодействия отдельных дисков с найденными реакциями в связях.

1.1.5. Произвести проверку правильности определения реакций в связях из условия равновесия всей расчетной схемы.

1.1.6. Построить эпюры поперечных сил и изгибающих моментов для отдельных дисков с объединением их для всей расчетной схемы.

Таблица 1.1

Исходные данные к задаче 1.1 РГР № 1

Первая цифра шифра	l1, м	q, кН/м	F, кН	Вторая цифра шифра	l2, м	l3, м	q1, кН/м	q2, кН/м	F1, кН	F2, кН	Третья цифра шифра (№ схемы)	a, м	b, м	c, м	d, м
		1,5
		2,5
		3,6					1,5
		2,4						1,5
		1,2					2,5
		1,8						2,5
		1,6

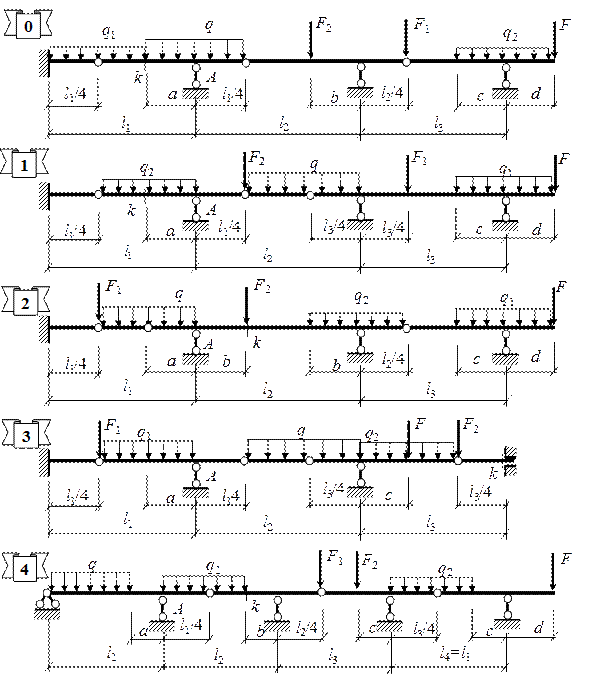
Рис. 1.1. Расчетные схемы 0 – 4 шарнирно-консольных балок

к задачам 1.1 и 2.1

1.1.7. Определить экстремальные значения изгибающих моментов в зонах действия распределенных нагрузок (при их наличии) и показать их значения и положения на эпюрах Q и M.

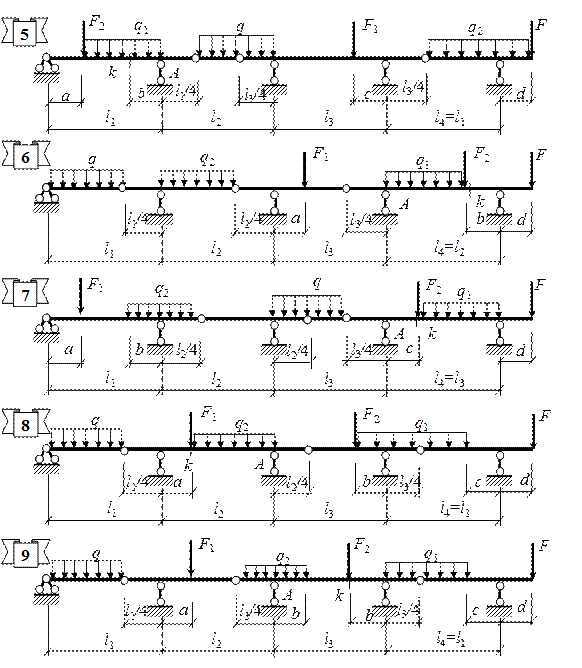
Рис. 1.2. Расчетные схемы 5 – 9 шарнирно-консольных балок

к задачам 1.1 и 2.1

1.1.8. Произвести проверку построения эпюр усилий. При правильном построении на каждом участке должно соблюдаться выполнение дифференциальных зависимостей

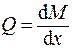и .

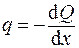Задача 1.2. Расчет рамы

Литература: [1, c. 113–124], [3, c. 63–66], [4, c. 38–42],

[5, c. 42–47], [6, c. 4–11, 49–53].

Исходные данные к задаче определяются по табл. 1.2 и схемам, представленным на рис. 1.3.

Таблица 1.2

Исходные данные к задаче 1.2 РГР № 1

Первая цифра шифра	M1, кН·м	M2, кН·м	Вторая цифра шифра	q1, кН/м	q2, кН/м	F1, кН	F2, кН	Третья цифра цифра (№ схемы)	l, м	h, м

Последовательность расчета

1.2.1. Произвести анализ геометрической неизменяемости заданной расчетной схемы.

Необходимым, но недостаточным условием геометрической неизменяемости, является выражение 3Д – 2Ш – С_оп = 0, где Д – количество дисков в расчетной схеме; Ш – количество простых шарниров или число связей, необходимых до полного защемления; С_оп – количество опорных связей.

Достаточное условие геометрической неизменяемости проверяется анализом геометрической структуры расчетной схемы.

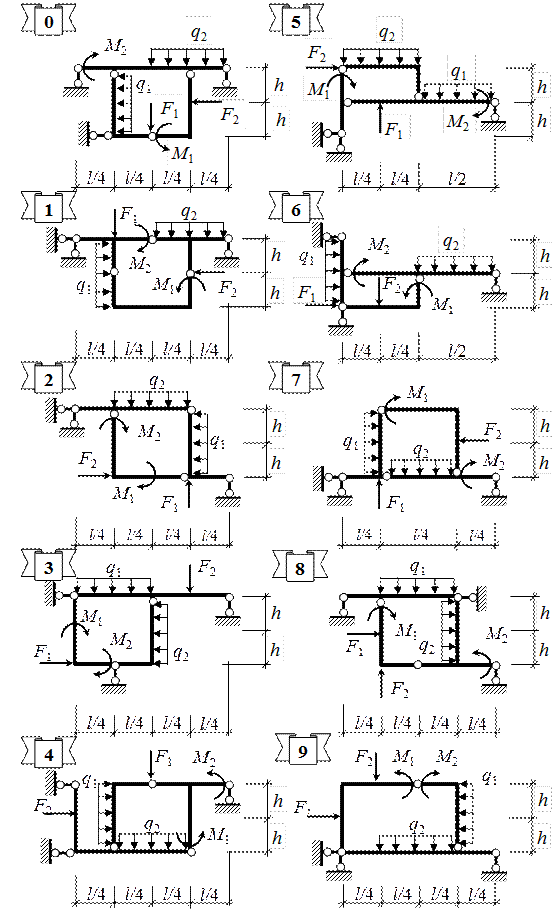Рис. 1.3. Расчетные схемы к задаче 1.2

1.2.2. Показать расчетную схему для определения реакций в опорных связях и определить эти реакции от действия заданной внешней нагрузки.

1.2.3. Показать расчетную схему для определения реакций внутренних связей. С этой целью замкнутый контур либо расчленяется по шарнирам на отдельные диски, либо при расчленении выделяется его трехшарнирная часть. Величины реакций в местах расчленения определяются из уравнений равновесия отдельных частей расчетной схемы.

1.2.4. Построить эпюры изгибающих моментов, поперечных и продольных сил. Эпюры можно построить сначала на отдельных частях расчетной схемы, а затем состыковать их в соответствии с заданной расчетной схемой.

1.2.5. Определить экстремальные значения изгибающих моментов в зонах действия распределенных нагрузок (при их наличии) и показать их значения и положение на эпюрах M и Q.

1.2.6. Произвести проверку построенных эпюр усилий. При правильном построении эпюр на каждом участке должны соблюдаться дифференциальные зависимост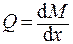и

и ,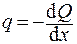

а любая отсеченная часть расчетной схемы и все ее узлы должны находиться в равновесии.