Интерполирование кубическими сплайнами

II. ЦЕЛЬ РАБОТЫ

Приобретение навыков использования интерполяционных сплайнов.

III. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть на 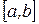в узлах сетки 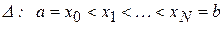заданы значения некоторой функции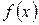

Для интерполирования функций воспользуемся кубическими сплайнами дефекта 1, которые обозначим 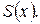На каждом из промежутков 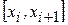сплайн 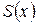записывается в виде

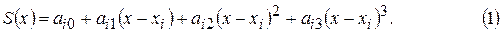
Причем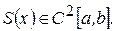

Рассмотрим два алгоритма построения интерполяционных кубических сплайнов, удовлетворяющих условиям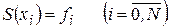

Введем обозначение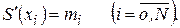

Решая систему уравнений

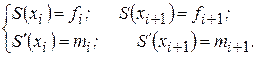
Найдем коэффициенты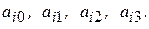

В результате выражение примет вид

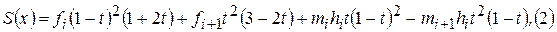где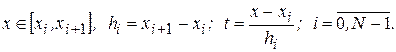

Кубический сплайн , записанный в терминах 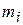, на каждом из промежутков 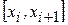непрерывен вместе со своей первой производной всюду на 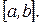Выберем величины 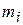так, чтобы была непрерывна и вторая производная сплайна. Условие

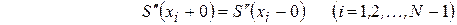
дает 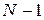уравнений для нахождения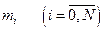

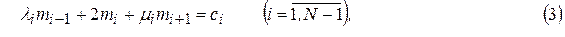
где

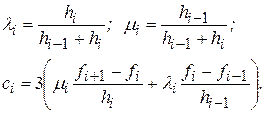
К уравнениям 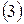следует присоединить еще два уравнения, являющихся краевыми условиями. Из полученной системы уравнений находятся значения величин 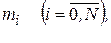которые подставляются в выражение для интерполяционного сплайна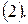

Если ввести обозначение 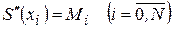и коэффициенты 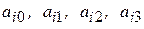найти как решение системы уравнений

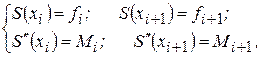
то на каждом 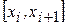интерполяционный кубический сплайн в терминах 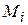будет представляться выражением

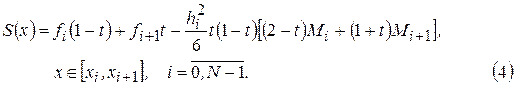
При этом сплайн 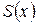и его вторая производная будут непрерывны на 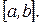Выберем величины 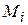так, чтобы была непрерывна и первая производная сплайна. Условие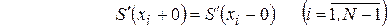

дает 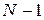уравнений

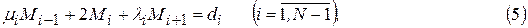
где

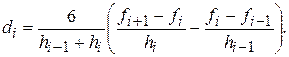
К уравнениям 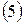следует присоединить два краевых условия. Из полученной системы уравнений находятся значения 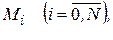которые подставляются в выражение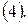

На практике наиболее употребительными являются краевые условия следующих типов:

I.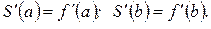

II.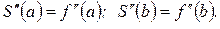

III.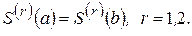

IV.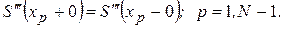

IV. ЗАДАНИЕ

С помощью интерполяционных кубических сплайнов, записанных в терминах 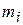и 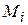, вычислить значения функции 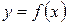в точках 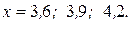Таблица значений функции 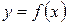приведена в лабораторной работе № 9.

Использовать следующие краевые условия

Указания:

1. При использовании сплайнов, записанных в терминах 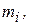к уравнениям 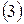присоединить следующие уравнения:

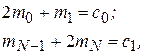
где

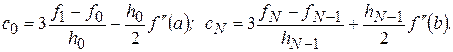
2. При использовании сплайнов, записанных в терминах 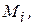к уравнениям 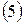присоединить следующие уравнения:

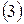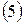3. Cистемы и являются системами с трехдиагональной матрицей. Осуществить их решение методом прогонки.

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Завьялов Ю.С., Квасов Б.И., Мирошниченко В.Л. Методы сплайн-функции. - М.: Наука, 1980. 248 с.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

Лабораторная работа № 11

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ

ПО ФОРМУЛЕ ТРАПЕЦИЙ

I. ЦЕЛЬ РАБОТЫ

Приобретение навыков приближенного вычисления интегралов с помощью квадратурных формул.

II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Пусть требуется вычислить интеграл .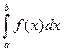

Разобьем отрезок 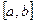с помощью равноотстоящих точек

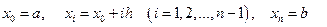
на 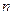равных частей. Шаг .

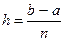Пусть = .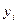

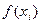Заменяя функцию 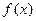многочленом Лагранжа

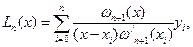
где ,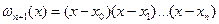

получаем квадратурную формулу

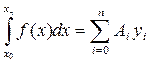. (1)

где

( ).

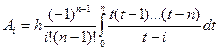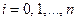При этом .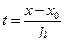

Полагая 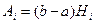, будем иметь

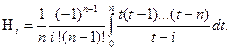(2)

Тогда квадратурная формула (1) принимает вид

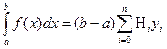. (3)

Формулы (2) и (3) называются формулами Ньютона – Котеса.

Полагая в формуле (2) 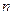=1, находим

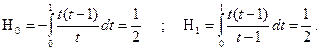
В результате получаем формулу трапеций

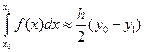. (4)

Для повышения точности на отрезке [a,b] вводится достаточно густая сетка

.

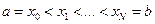Интеграл разбивается на сумму интегралов по шагам сетки и к каждому шагу применяют формулу (4).

Обобщенная формула трапеций на равномерной сетке с шагом 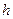имеет вид

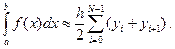(5)

Для равномерной сетки справедлива следующая мажорантная оценка погрешности формулы трапеций:

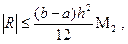
где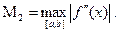

III. ЗАДАНИЕ

Вычислить с помощью формулы трапеций определенный интеграл от заданной функции.

Варианты заданий

№	f(x)	Пределы интегрирования
a	b
1.		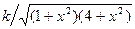0,1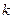
2.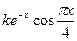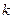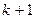
3.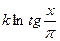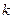
4.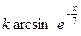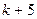
5.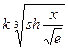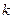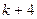
6.		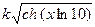	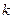3,2
7.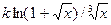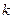
8.
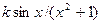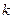9.
10.
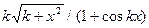11.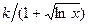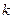
12.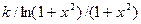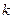
13.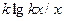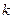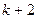
14.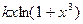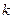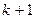
15.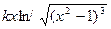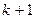
16.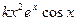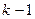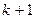
17.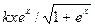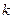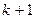
18.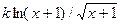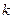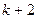
19.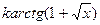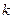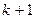
20.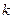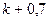
21.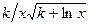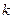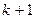
22.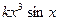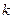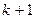
23.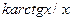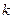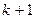
24.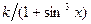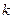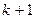
25.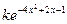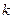

Здесь k-последняя цифра номера группы.

Указание: При вычислении интеграла положить h=0.1

IV. Оформление отчета

В отчете должны быть представлены:

1. Название работы.

2. Постановка задачи.

3. Описание алгоритма (метода) решения.

4. Текст программы с описанием.

5. Результаты работы программы.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.

2. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.

3. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.

Лабораторная работа № 12