Решение нелинейного уравнения методом
ДИХОТОМИИ
I. ЦЕЛЬ РАБОТЫ
Приобретение навыков нахождения с заданной погрешностью корней нелинейного уравнения.
II. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Требуется найти корни уравнения
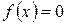, (1)
где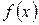 
- непрерывная функция.
Пусть нашли такие точки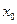 
и 
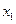, что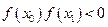 
, то есть на отрезке [ 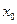, 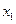] лежит по меньшей мере один корень. Найдем середину отрезка [ , ] 
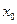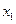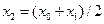и вычислим 
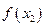. Если 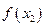=0, то 
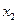есть корень 
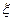. Если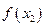 
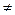0, то из двух половин отрезка [ 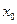, 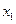] выберем ту, для которой 
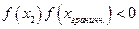, так как один корень лежит на этой половине. Затем новый отрезок делим пополам и выбираем ту половину, на концах которой функция 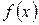имеет разные знаки. И так далее.
Деление продолжаем до тех пор, пока длина очередного отрезка, где лежит корень, не станет меньше 2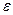 
, где 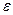- заданная погрешность. Тогда середина последнего отрезка даст значение корня с требуемой точностью.
III. ЗАДАНИЕ
Найти методом дихотомии один из действительных корней уравнения 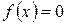с погрешностью 
.
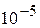Варианты задания:
| № | Уравнение |
 | |
  | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 |
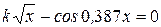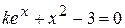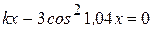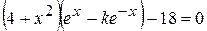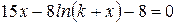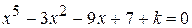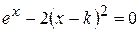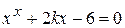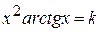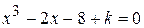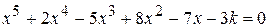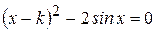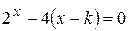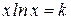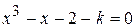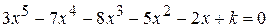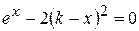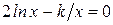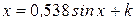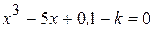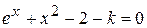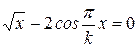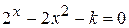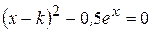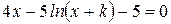Здесь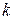 
- последняя цифра номера группы, 
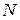- номер фамилии студента в журнале группы.
IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
Лабораторная работа № 7
РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ МЕТОДОМ
ИТЕРАЦИИ
II. ЦЕЛЬ РАБОТЫ
Приобретение навыков нахождения с заданной погрешностью корней нелинейного уравнения.
III. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Требуется найти корни уравнения
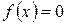, (1)
где 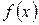- непрерывная функция.
Заменим исходное уравнение эквивалентным ему уравнением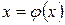 
.
Выберем некоторое нулевое приближение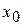 
и вычислим дальнейшие приближения по формуле
( 
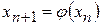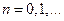). (2)
Если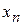 
стремится к некоторому пределу 
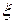, то этот предел есть корень исходного уравнения, т.е.
.
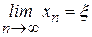Исследуем условия сходимости. Если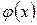 
имеет непрерывную производную, тогда (по теореме Лагранжа)
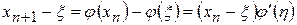, (3)
где точка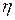 
лежит между точкам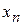и и 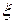. Поэтому, если всюду на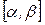 
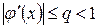, то отрезок 
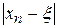убывает не медленней членов геометрической прогрессии со знаменателем 
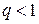и последовательность 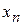сходится при любом начальном приближении 
.
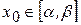Действительно, это видно из соотношений
.
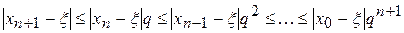Очевидно, чем меньше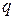 
, тем быстрее сходимость. Успех метода зависит от того, насколько удачно выбрано .
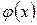Из выражения (3) видно, что, если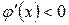 
, то итерации попеременно оказываются то с одной, то с другой стороны 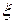, так что корень заключен в интервале 
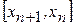. Это надежная, хотя несколько грубая оценка. Но она неприменима, когда 
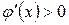, когда итерации сходятся к корню монотонно, т.е. с одной стороны.
Можно показать, что итерации следует прекращать, если выполняется условие
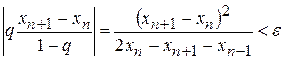, (4)
где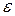 
- заданная точность.
Метод итераций имеет важное достоинство самоисправляемости. Ошибки вычислений в методе не накапливаются. Метод итераций устойчив даже к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости. Ошибочное приближение рассматривается как некоторое новое начальное.
IV. ЗАДАНИЕ
Найти методом итераций один из действительных корней уравнения 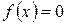с допустимой погрешностью .
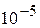Варианты задания приведены в лабораторной работе № 6.
IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.
Лабораторная работа № 8