Решение систем линейных уравнений
МЕТОДОМ ПРОСТОЙ ИТЕРАЦИИ
I. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения систем линейных алгебраических уравнений итерационными методами.
II. ТЕОРЕТИЧЕСКАЯ СПРАВКА
Рассмотрим метод простой итерации.
Пусть дана система линейных алгебраических уравнений
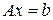
с неособенной матрицей (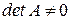 
). Согласно методу простой итерации ее предварительно приводят к виду
,
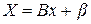где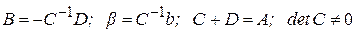 
, т.е. первое уравнение системы разрешили относительно 
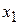, второе - относительно 
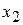и т.д.
Предположим, что известно начальное приближение
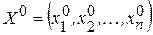
к точному решению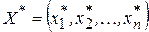 
системы. Тогда все следующие приближения найдем по формуле
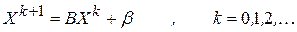
Если последовательность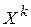 
сходится к некоторому предельному вектору 
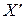, то он будет решением системы. Действительно, считая 
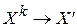при 
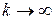, получаем из выражения
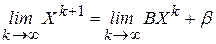
равенство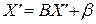 
.
Последовательность 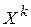в методе простой итерации сходится, если для матрицы 
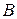выполняется одно из неравенств
1) 
;
.
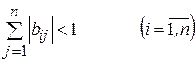III. ЗАДАНИЕ
Найти решение системы линейных уравнений, приведенной в лабораторной работе №1. При решении системы использовать метод простой итерации.
IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.
Лабораторная работа № 3
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
МЕТОДОМ ЗЕЙДЕЛЯ
II. ЦЕЛЬ РАБОТЫ
Приобретение навыков решения систем линейных алгебраических уравнений итерационными методами.
III. ТЕОРЕТИЧЕСКАЯ СПРАВКА
Рассмотрим метод Зейделя.
Пусть система 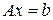приведена к канонической форме
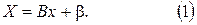
В методе простой итерации следующее приближение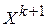 
находится по предыдущему 
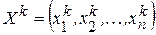путем подстановки 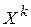в правую часть (1). При этом порядок выбора уравнений значения не имеет.
Согласно методу Зейделя осуществляется разумный выбор порядка уравнений для подстановок и немедленный ввод в вычисления каждого из полученных приближений для неизвестных.
Предположим, что для перехода от приближения 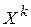к 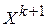выбран какой-то порядок привлечения уравнений для подстановок. Изменяя, если необходимо, нумерацию уравнений и неизвестных, можно считать, что уравнения для подстановок берутся в порядке роста их номеров. Для каждого шага порядок привлечения уравнений может быть своим. Перестановка уравнений и изменение нумераций влекут изменение матрицы 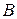и вектора 
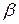. Чтобы отметить это, обозначим 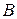и 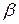для рассматриваемого шага через 
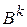и 
.
И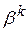терация в методе Зейделя выполняется в следующем порядке:
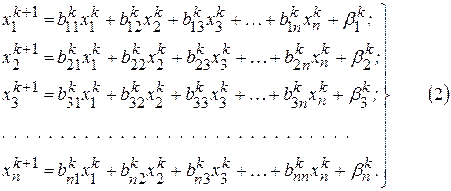
После нахождения вектора 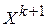устанавливается порядок подстановок в уравнения значений 
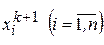и переходят к вычислению вектора 
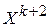и т.д.
Приведем теперь принцип установления порядка привлечения уравнений для подстановок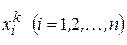 
. Можно пытаться улучшить ту составляющую решения, которая найдена наименее точно, чтобы при нахождении всех других составляющих употребить улучшенное ее значение.
О точности 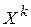можно судить по вектору поправки на шаге 
: 
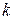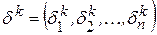, где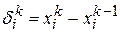 
. Величины поправок составляющих нумеруют в порядке убывания их модулей, и в том же порядке вычисляют составляющие следующего приближения 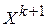, сначала ту составляющую, которая отвечает наибольшей по модулю поправке, и т.д.
Рассмотрим более подробно стационарный метод Зейделя, когда при итерациях порядок уравнений сохраняется, а следовательно, сохраняются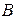 
и 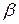. Вычисления по-прежнему проводят по формуле (2).
Разложим матрицу 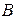на сумму двух матриц 
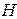и 
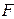, где
, 
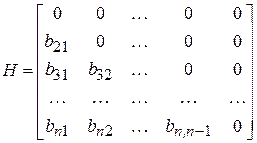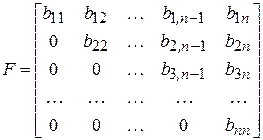
Тогда равенства (2) можно записать в матричной форме в виде
.
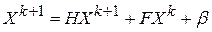Отсюда следует, что
,
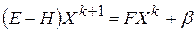а так как определитель матрицы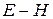 
равен единице и она имеет обратную матрицу, то равенство (2) равносильно
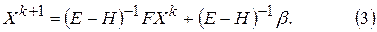
Поэтому стационарный метод Зейделя равносилен методу простой итерации, примененному к системе
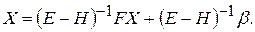
Последовательность 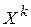в стационарном методе Зейделя сходится, если для матрицы 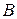выполняется одно из неравенств
2) ;
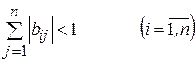3) .
IV. ЗАДАНИЕ
Найти решение системы линейных уравнений, приведенной в лабораторной работе №1. При решении системы использовать стационарный метод Зейделя.
IV. Оформление отчета
В отчете должны быть представлены:
1. Название работы.
2. Постановка задачи.
3. Описание алгоритма (метода) решения.
4. Текст программы с описанием.
5. Результаты работы программы.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Демидович Б.П., Марон И.А. Основы вычислительной математики. - М.: Лань, 2009. 672 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. — М.: БИНОМ. Лаборатория Знаний, 2007 636с.
3. Калиткин Н.Н. Численные методы. - М.: Наука, 1978. 512 с.
4. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы. Т.1. - М.: Наука, 1976. 350 с.
Лабораторная работа № 4