Исследование устойчивости по критерию Михайлова

Цель работы

Целью работы является изучение методов оценки устойчивости САР, исследование устойчивости системы с помощью частотного критерия Михайлова.

Общие сведения

Устойчивость– это свойство системы возвращаться в исходное состояние равновесия после снятия воздействия, выведшего систему из этого состояния.

Признаки (условия) устойчивости линейной системы:

а) физический – система устойчива, если свободная составляющая y_св(t) переходного процесса с увеличением времени стремится к нулю, неустойчива – если она стремится к бесконечности, и нейтральна, если она стремится к некоторой постоянной величине;

б) математический – для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную действительную часть (все полюса системы были левыми). Система находится на апериодической границе устойчивости, если при остальных левых корнях имеет один нулевой корень, и на колебательной (периодической) границе устойчивости, если при остальных левых корнях характеристического уравнения имеет пару чисто мнимых корней. Характеристическое уравнение образуется из знаменателя передаточной функции системы D(s) = 0.

При невозможности вычислить корни используют косвенные признаки их положения относительно мнимой оси – критерии устойчивости. Алгебраические критерии (Гурвица, Рауса) оценивают устойчивость системы по значениям коэффициентов характеристического уравнения, частотные критерии (Михайлова, Найквиста) – по виду частотных характеристик системы.

Критерий Михайлова основан на исследовании характеристической функции D(jω) = U(ω) + jV(ω), полученной из характеристического многочлена подстановкой s = jω.

Основная формулировка: система n-го порядка устойчива, если кривая Михайлова, начинаясь при w=0 на действительной положительной полуоси, проходит при изменении частоты w от нуля до плюс бесконечности последовательно против часовой стрелки n квадрантов комплексной плоскости.

Дополнительная формулировка (следствие или форма 2): система n-го порядка устойчива, если четная U(w) и нечетная V(w) функции при изменении частоты w от нуля до плюс бесконечности обращаются в нуль поочередно n раз, начиная с нечетной функции, т.е. их корни перемежаются. Для построения графика используется та же таблица частот, что и в основной форме.

Указания к работе

Предварительно следует найти главную передаточную функцию системы (рисунок 1) W_yr(s) по выходу y относительно входа r с учетом параметров блоков 5 и 6 – сначала в общем виде, затем с численными значениями данных по своему варианту (значение коэффициента обратной связи k _ос принять равным единице).

Используя программу MICHCHAR "Критерий Михайлова" из библиотеки LinCAD и характеристическое уравнение системы (знаменатель передаточной функции), необходимо получить кривую Михайлова на комплексной плоскости (рисунок 5) с таблицей частот, соответствующих пересечениям кривой с осями координат и крайним точкам кривой по каждой оси. Кривая Михайлова представляет собой раскручивающуюся спираль, уходящую в бесконечность. Поэтому диапазон частот следует подобрать экспериментально, от нуля до значения частоты, при котором кривая последний раз пересекает какую-либо ось, для более точного определения координат пересечения действительной и мнимой осей и желаемого вида кривой Михайлова.

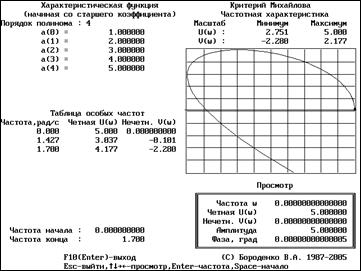
Рисунок 5

Таблица особых частот включает только минимум точек, поэтому, пользуясь перемещающимся маркером, желательно определить координаты точек, соответствующих наибольшим отклонениям по действительной или мнимой оси, и добавить их в таблицу. По расширенной таблице нужно построить кривую Михайлова в произвольном масштабе, по ее виду дать заключение об устойчивости системы. Если какой-либо оси не оказалось на графике, ее следует дорисовать приближенно, а на кривой поставить стрелку в сторону увеличения частоты.

Самостоятельно, используя полученную таблицу частот, построить графики четной U(ω) и нечетной V(ω) функций в соответ­ствии со второй формой (следствием) критерия Михайлова, проверить сделанный ранее вывод об устойчивости системы. На всех графиках обязательно указывать порядок системы (полинома) n.

3.4 Методический пример

Характеристическое уравнение САР

D(s) = s⁴ + 2s³ + 3s² + 4s + 5 = 0.

Расширенная таблица частот

ω, рад/с	U(ω)	V(ω)
0.000	5.000	0.000
0.800	3.490	2.176
1.230	2.750	1.198
1.427	3.037	-0.101
1.700	4.177	-2.280

Годограф характеристической функции D(jω)

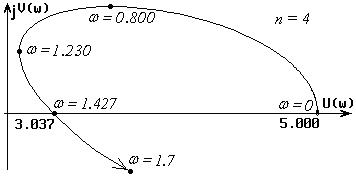
Система неустойчива, поскольку кривая Михайлова, начинаясь на положительной действительной оси, не проходит последовательно против часовой стрелки n квадрантов комплексной плоскости, где n=4 – порядок системы.

Графики четной и нечетной функций

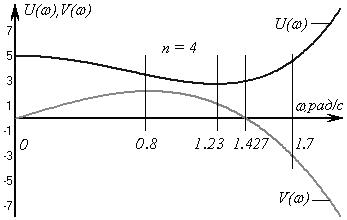
Система неустойчива, поскольку графики четной U(ω) и нечетной V(ω) функций, начинаясь с V(ω) = 0, не пересекают при возрастании частоты ось частот поочередно (число пересечений меньше n).

Содержание отчета

Отчет по лабораторной работе должен содержать название, цель работы, главную передаточную функцию системы в общем виде и после подстановки численных значений, характеристическое уравнение системы, полученные на ЭВМ таблицу частот и кривую Михайлова, построенный самостоятельно график четной и нечетной функций с заключением об устойчивости системы. На всех графиках должны быть указаны значения параметров в точках пересечения кривых с осями координат, порядок системы, обозначены оси и каждая кривая при количестве характеристик более одной.

К защите знать физический и математический признаки устойчивости систем, названия основных критериев устойчивости, формулировку критерия Михайлова и его следствия, методику построения кривой Михайлова вручную.

4 Выбор параметров регулятора методом D-разбиения

Цель работы

Целью работы является изучение методов проектирования систем с достижением заданных параметров устойчивости, в частности, метода D-разбиения по двум параметрам.

Общие сведения

Метод используется при синтезе систем для определения допус­тимых по условиям устойчивости пределов изменения некоторых па­раметров системы – обычно коэффициента усиления k или постоян­ной времени T регулятора.

Процесс построения в пространстве параметров системы об­ластей с разным числом правых корней характеристического урав­нения называется D-разбиением.

Областью устойчивости D(0) называют область в пространстве изменяемых параметров, каждой точке которой соответствуют только левые корни характеристического уравнения. Остальные D-области отличаются числом правых корней характеристического уравнения и обозначаются соответственно D(1) – область с одним правым полю­сом, D(2) – с двумя и т.д.

Граница любой D-области является отображением мнимой оси плоскости корней, она соответствует совокупности значений парамет­ров, при которых хотя бы один корень характеристического уравне­ния системы находится на мнимой оси.

Если система в пространстве всех своих параметров не имеет области устойчивости, она является структурно неустойчивой. На практике используют D-разбиение по одному параметру (результатом является отрезок на условной плоскости) и по двум параметрам (ре­зультатом является плоскость).

В случае D-разбиения по одному параметру все построения производят, изменяя значения одного параметра при постоянстве остальных. Чтобы получить плоскость, вещественный параметр искусственно делают двумерным, заменяя s = jw с образованием мнимой оси, однако окончательным результатом является отрезок на действительной оси.

Подставив s = jw в характеристическое уравнение системы, раз­решают его относительно изменяемого параметра, находят четную (действительную) U(w) и нечетную (мнимую) V(w) функции. Изменяя частоту w от 0 до плюс бесконечности, строят кривую D-разбиения и ее зеркальное отображение относительно действительной оси. Двига­ясь по кривой от точки w = -¥ до точки w = +¥ , наносят штриховку слева от кривой. (Напомним, что кривая D-разбиения является ото­бражением мнимой оси, а при движении по этой оси от -j¥ к +j¥ об­ласть устойчивости на плоскости корней располагается слева).

Направление штриховки указывает на область с наибольшим числом левых корней. При каждом переходе через кривую навстречу штриховке один корень характеристического уравнения становится правым, в обратном направлении – левым. Выбранную область-пре­тендент D(0) проверяют на устойчивость с помощью любого крите­рия, подставив значение параметра из этой области в характеристиче­ское уравнение. Поскольку изменяемый параметр является действи­тельной величиной, его допустимые значения лежат на отрезке дейст­вительной оси, заключенном внутри области устойчивости D(0).

Критическим называется значение параметра системы или коэффициента характеристического уравнения, при котором система находится на границе устойчивости.

Для проверки области-претендента на устойчивость системы четвертого порядка удобен критерий Гурвица, у которого должны выполняться два условия: необходимое – все коэффициенты характеристического уравнения положительны, и достаточное – определитель третьего порядка D₃ = a₃D₂ – a₁²a₄ = a₃·(a₁×a₂ - a₀×a₃) – a₁²a₄ > 0.

Указания к работе

В работе производится выбор значения коэффициента усиления k₁ регулятора, вошедшего в коэффициент характеристического уравнения a_n, по условию устойчивости системы при номинальных значениях остальных коэффициентов.

Предварительно следует выразить аналитически зависимость коэффициента характеристического уравнения a_n от коэффициента k₁.

Используя программу DRAZBTWO "D-разбиение по двум параметрам" из библиотеки LinCAD и характеристическое уравнение системы из предыдущей работы, получить на плоскости параметров область устойчивости при изменении в заданном диапазоне коэффициента a_n и одного из коэффициентов a₁ - a_n-1, оставив номинальными значения остальных коэффициентов. Какой из коэффициентов a₁ - a_n-1 лучше выбрать для изменения, подбирают экспериментально по наиболее характерному проявлению областей устойчивости, при этом его значение рекомендуется задавать в пределах 0.9-1.1 номинального.

На линии, соответствующей номинальному значению неосновного коэффициента a₁ - a_n-1, определить критическое значение a_{n, кр} , соответствующее пересечению границы области устойчивости, а в самой области устойчивости выбирается желаемое значение a_n приблизительно равноудаленным от границ области (рисунок 6).

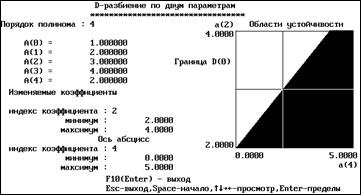
Рисунок 6

Самостоятельно оценить устойчивость системы по критерию Гурвица после подстановки выбранного значения a_n в характеристическое уравнение. Если устойчивость системы обеспечивается, по выбранной величине a_n найти значение k₁, которое должно использоваться во всех последующих работах взамен первоначально заданного. При нулевом значении k₁ следует немного изменить выбранное значение a_n.

4.4 Методический пример

Характеристическое уравнение системы

D(s) = a₀ s⁴ + a₁s³ + a₂ s² + a₃ s + a₄= s⁴ + 2s³ + 3s² + 4s + 2 = 0

Области устойчивости в пространстве коэффициентов 2 < a₂ < 4 и 0 < a₄ < 5

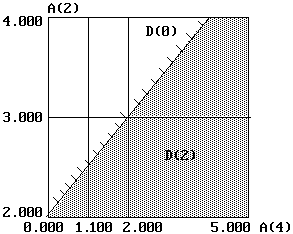
При номинальной величине a₂ = 3 критическое значение a_{4, кр1} = 0 в сторону уменьшения и a_{4, кр2} = 2 в сторону увеличения, оптимальное значение по устойчивости выбираем равным a₄ = 1.1.

Для проверки области-претендента на устойчивость по критерию Гурвица подставляем выбранное значение в характеристическое уравнение:

- характеристическое уравнение D(s) = s⁴ + 2s³ + 3s² + 4s + 1.1 = 0;

- условие D₃ = a₃·(a₁×a₂ - a₀×a₃) – a₁²a₄ = 8 – 4.4 =∙3.6 > 0 выполняется.

Принимая значение a₄ = 1.1, находим необходимое значение коэффициента k₁ = (a₄ – 1)/k₂/k₃ = (1.1 – 1)/(0.1∙10) = 0.1.

Рассчитанная с новым значением k₁ передаточная функция САР

.

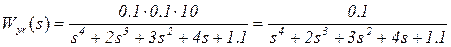Содержание отчета

Отчет по лабораторной работе должен содержать цель работы, характеристическое уравнение системы D(s) = 0, полученный на ЭВМ график областей D-разбиения с обозначением величин и масштаба по обеим осям, обозначением областей D( ) и штриховкой в сторону области устойчивости, визир с координатами выбранной точки, критическое значение a_{n, кр}, выбранное значение a_n, проверку устойчивости системы при этом значении по критерию Гурвица, зависимость a_n от коэффициента k₁, рассчитанное значение k₁ и вид передаточной функции системы после подстановки k₁.

К защите знать основные определения метода D-разбиения по одному параметру, порядок построения кривых, штриховки, выбора параметра, формулировки и порядок применения критериев Гурвица и Рауса, определение для критического параметра.