Генератор (блок 5) описывается дифференциальным уравнением

Республики Казахстан

Казахский агротехнический университет им. С.Сейфуллина

Кафедра

электроснабжения

ТЕОРИЯ

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Лабораторный практикум

В методических указаниях к лабораторному практикуму приво­дятся рекомендации по выполнению лабораторных работ, исходная схема моделируемой системы и варианты заданий, изложены после­довательность выполнения работ и порядок оформления отчета.

В качестве среды для компьютерного моделирования используется библиотека программ LinCAD.

Содержание

	Задание
	Исследование временных характеристик фильтра
	Исследование частотных характеристик фильтра
	Исследование устойчивости по критерию Михайлова
	Выбор параметров регулятора методом D-разбиения
	Коррекция системы методом корневого годографа
	Исследование прямых оценок качества регулирования
	Оценка запасов устойчивости системы регулирования
	Литература
	Приложение А

Задание

Структурная схема системы автоматического регулирования (САР) напряжения генератора постоянного тока (рисунок 1).

Рисунок 1

Генератор (блок 5) описывается дифференциальным уравнением

Исходные данные (таблица 1).

Таблица 1

Пара­метр	Вариант (выбирается согласно номеру по порядку в списке группы)
1, 11	2, 12	3, 13	4, 14	5, 15	6, 16	7, 17	8, 18	9, 19	10, 20
k1	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1.7	1,8	1,90
k2	12,0	11,0	10,0	9,0	8,0	7,0	6,0	5,0	4,0	3,00
k3	равен порядку первой буквы фамилии в алфавите
T1	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0	10,00
T2	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,00
T3	0,5	0,8	1,1	1,4	1,7	1,5	1,2	1,0	0,8	0,60
x	0,9	0,8	0,8	0,6	0,6	0,4	0,4	0,2	0,2	0,15

Примечание – точность расчетов не менее трех знаков после запятой. Все вычисления и графические построения выполняются в соответствии с теоретическими положениями, изложенными в [1-4] и конспекте лекций. Для обработки на ЭВМ используется пакет программ LinCAD. Последовательно выполняя работы, необходимо спроектировать устойчивую САР с заданными показателями качества.

Оформление отчета к лабораторной работе должно удовлетворять требованиям стандарта ПГУ. Допускается выполнять общий от

Цель работы

Целью работы является исследование реакции на типовое воздействие во временной области звеньев (фильтров) с разной передаточной функцией.

Общие сведения

Регулярные сигналы, используемые для исследования САР, называются типовыми воздействиями. Они позволяют сравнивать свойства различных систем при равных начальных условиях и входных сигналах одинаковой формы. К типовым обычно относятся ступенчатое (скачок) A∙1(t) или функция Хевисайда, импульсное A∙δ(t) или функция Дирака, гармоническое A∙sinωt и степенное A∙tⁿ воздействия (функции). При А = 1 воздействие называется единичным.

Любую функцию времени с допустимой погрешностью можно разложить на совокупность типовых воздействий с соответствующими коэффициентами веса. Тогда по принципу суперпозиции реакция на это воздействие определится как сумма реакций линейной системы на отдельные воздействия, принцип вычисления которых известен.

Переходной функцией h(t) называется реакция системы на еди­ничный скачок 1(t) при нулевых начальных условиях. Реакция на скачок произвольной величины называется кривой разгона.

Импульсной (весовой) функцией g(t) называется реакция систе­мы на единичный импульс δ(t) при нулевых начальных условиях.

Основным инженерным методом решения дифференциальных уравнений, т. е. исследования поведения САР во времени, является преобразование Лапласа, которое операции дифференцирования и интегрирования заменяет более простыми алгебраическими операциями умножения и деления на комплексную переменную s. Операторная передаточная функция (ПФ) является основной формой описания систем в операторной области по методу один вход, один выход.

Передаточной функцией W(s) называется отношение изображений по Лапласу выходной величины Y(s) к входной X(s) при нулевых начальных условиях. Обычно m ≤ n, где n – порядок системы.

По дифференциальному уравнению системы составим ПФ W(s)

,

.

В соответствии с теоремами о начальном и конечном значениях функции времени (оригинала) начальное и конечное (установившееся) значения переходной характеристики равны отношению коэффициентов при s в степени n числителя и знаменателя передаточной функции в первом случае, и отношению свободных членов ПФ (коэффициенту усиления в установившемся режиме k(∞) или k_уст) во втором.

Начальное значение:

Конечное значение: .

Указания к работе

Предварительно необходимо для фильтра, входящего в состав регулятора (рисунок 1) и состоящего из звеньев 1-4 , вычислить передаточные функции по выходам a, b, c, d относительно входа e сначала в общем виде, а затем с учетом численных значений своего варианта (таблица 1), используя правила структурных преобразований (приложение А).

Для получения экспериментальных переходных характеристик фильтра используется программа TIMECHAR "Временные характеристики" из библиотеки LinCAD (рисунок 2). Поочередно вводят передаточные функции фильтра W_ae(s), W_be(s), W_ce(s), W_de(s) для выходов a, b, c и d на ЭВМ – сначала порядок полинома числителя и его коэффициенты, начиная со старшего, затем порядок полинома знаменателя и его коэффициенты, включая нулевые. Не забывайте, что разделителем целой и дробной частей числа у программ LinCAD является точка.

Рисунок 2

На вход фильтра подают сигнал в виде единичного скачка 1(t) и зарисовывают полученный график переходной характеристики h(t) в масштабе рядом с соответствующей передаточной функцией, определяя числовые значения всех характерных точек (начальное, конечное значения, максимум, минимум). Длительность периода исследования подбирают экспериментально так, чтобы в конце графика переходный процесс заканчивался (кривая шла горизонтально), но в то же время все параметры начальной части характеристики легко определялись. Начать подбор можно с 50-80 секунд, затем уменьшать значение до оптимального. Учитывая периодический характер сигнала, допускается зарисовывать вид реакции только за первую половину периода.

Каждый раз входное воздействие разлагается в ряд Фурье

,

постоянная составляющая a₀, частота первой гармоники ω и коэффи­циенты A_k, B_k части гармоник которого (не более пятнадцати) выво­дятся для иллюстрации на экран. Поскольку отклик фильтра является суммой реакций на гармонические воздействия, число m которых ог­раничено, отсутствие высших гармоник может искажать начальную часть кривой – снижать ее максимальное значение при t = 0.

1.4 Методический пример

Передаточная функция фильтра по выходу a относительно входа e

.

Переходная характеристика h_aе(t) должна иметь начальное значение b₀/a₀ = 3.2/2 = 1.6 и конечное значение b_m/a_n = 1.6/1 = 1.6.

Содержание отчета

Отчет по лабораторной работе должен содержать название, цель работы, структурную схему фильтра с обозначениями входа и выходов, затем для каждого типа фильтра – передаточную функцию в общем виде и после подстановки численных значений, рядом полученную переходную характеристику h(t) в масштабе, с числовыми данными и обозначениями.

К защите знать назначение преобразования Лапласа, правила вычисления передаточной функции по структурной схеме, все типовые воздействия и временные характеристики. Уяснить взаимосвязь вида передаточной функции и соответствующей переходной характеристики фильтра с учетом свойств преобразования Лапласа, т.е. правил вычисления начального и конечного значений оригинала, уметь по виду передаточной функции представить вид переходной характеристики и наоборот.

Цель работы

Целью работы является изучение типовых частотных характеристик САР, исследование реакции на гармоническое воздействие в частотной области звеньев (фильтров) с разной передаточной функцией.

Общие сведения

Основной формой описания систем в частотной области является частотная передаточная функция или комплексный коэффициент передачи

.

Зависимости отношения амплитуд A(w) и разности фаз j(w) выходного и входного гармонического сигналов системы от частоты w в установившемся режиме называются соответственно амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. АЧХ начинается при значении b_m/a_n = k_уст и заканчивается в нуле (для m<n) или при b₀/a₀ (для m= n). P(ω) = ReW(jω) или вещественная частотная характеристика (ВЧХ) соответствует проекции вектора W(jω) на действительную ось, Q(ω) = ImW(jω) или мнимая частотная характеристика (МЧХ) соответствует проекции вектора W(jω) на мнимую ось.

Обобщающей является амплитудно-фазовая частотная характе­ристика (АФЧХ или просто АФХ) – графическое изображение частот­ной передаточной функции W(jω) на комплексной плоскости.

Кривая (годограф), которую чертит на комплексной плоскости конец вектора при изменении частоты ω от 0 до +∞, на­зывается АФЧХ.

Реакцию системы на гармоническое воздействие любой частоты ω в показательной форме получают путем умножения на А(ω) при этой частоте амплитуды входного сигнала и добавления φ(ω) к его фазе.

Частотные характеристики системы можно изменять желаемым образом с помощью специальных корректирующих звеньев (фильтров). Фильтром называется четырехполюсник, предназначенный для выделения из состава сложного входного сигнала частотных составляющих, расположенных в полосе пропускания, и подавления частотных составляющих, расположенных в полосе задерживания.

В зависимости от взаимного расположения полос пропускания и задерживания различают (рисунок 3):

а б в г

Рисунок 3

а) фильтр низких частот (ФНЧ) с полосой пропускания от нуля до w₂ и полосой задерживания от частоты w_з2 > w₂ до бесконечности;

б) фильтр верхних частот (ФВЧ) с полосой пропускания от частоты w₁ до бесконечности и полосой задерживания от нуля до частоты w_з1 < w₁;

в) полосовой фильтр (ПФ) с полосой пропускания, заключенной между частотами w₁ и w₂ и полосой задерживания частот меньших, чем w_з1, и больших, чем w_з2;

г) заграждающий (режекторный) фильтр (РФ) с полосой задерживания, заключенной между частотами w_з1 и w_з2, и полосой пропускания частот меньших, чем w₁, и больших, чем w₂.

Указания к работе

Используя программу FREQCHAR "Частотные характеристики" из библиотеки LinCAD (рисунок 4) и рассчитанные в предыдущей работе передаточные функции фильтра по выходам a, b, c, d относительно входа e, получить на ЭВМ (для логарифмического масштаба изменения частоты) и зарисовать в отчет АЧХ и ФЧХ для каждой передаточной функции. Начальное и конечное значения частот подбирают экспериментально, так, чтобы существенное изменение АЧХ приходилось примерно на середину графика, а в левой и правой части графика АЧХ была горизонтальной (можно начать подбор с частот 0.01 и 100).

Рисунок 4

Найти для каждого типа фильтра полосы пропускания и задерживания, построив по реальным характеристикам асимптотические (прямолинейные) и определив по точкам пересечения отрезков частоты сопряжения (граничные частоты полос), обозначить, какому типу фильтра соответствует каждая передаточная функция и график. Касательные к горизонтальным и наклонным участкам АЧХ (асимптоты) можно строить прямо на экране монитора, совмещая с получаемыми графиками линейку. Значения характеристик для конкретной точки получают в окне просмотра, перемещая стрелками курсора указатель по рабочему полю к месту сопряжения отрезков (касательных).

2.4 Методический пример

Передаточная функция фильтра по выходу a относительно входа e

.

Полученные амплитудная и фазовая частотные характеристики соответствуют заграждающему фильтру (РФ) с полосой задерживания на частоте ω_з = 0.697 рад/с, полосой пропускания менее частоты ω₁ = = 0.032 рад/с и более частоты ω₂ = 1.462 рад/с. Начальное значение АЧХ равно b_m/a_n = 1.6/1 = 1.6, конечное b₀/a₀ = 3.2/2 = 1.6.

Содержание отчета

Отчет по лабораторной работе должен содержать название, цель работы, для каждого из четырех фильтров рассчитанную передаточную функцию и полученную характеристику в масштабе с измеренными значениями амплитуды в характерных точках, частотами пропускания, задерживания и другими необходимыми обозначениями.

К защите знать все виды частотных характеристик, их смысл, методы вычисления и построения, формулировки, типы фильтров и вид их характеристик. Уяснить связь вида передаточной функции и соответствующей амплитудной частотной характеристики, т.е. уметь по виду передаточной функции построить АЧХ фильтра в соответствующем масштабе. Уметь определить с помощью АЧХ выходной сигнал по входному для заданной частоты и типа фильтра. Объяснить названия полос пропускания и задерживания.

Цель работы

Целью работы является изучение методов оценки устойчивости САР, исследование устойчивости системы с помощью частотного критерия Михайлова.

Общие сведения

Устойчивость– это свойство системы возвращаться в исходное состояние равновесия после снятия воздействия, выведшего систему из этого состояния.

Признаки (условия) устойчивости линейной системы:

а) физический – система устойчива, если свободная составляющая y_св(t) переходного процесса с увеличением времени стремится к нулю, неустойчива – если она стремится к бесконечности, и нейтральна, если она стремится к некоторой постоянной величине;

б) математический – для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную действительную часть (все полюса системы были левыми). Система находится на апериодической границе устойчивости, если при остальных левых корнях имеет один нулевой корень, и на колебательной (периодической) границе устойчивости, если при остальных левых корнях характеристического уравнения имеет пару чисто мнимых корней. Характеристическое уравнение образуется из знаменателя передаточной функции системы D(s) = 0.

При невозможности вычислить корни используют косвенные признаки их положения относительно мнимой оси – критерии устойчивости. Алгебраические критерии (Гурвица, Рауса) оценивают устойчивость системы по значениям коэффициентов характеристического уравнения, частотные критерии (Михайлова, Найквиста) – по виду частотных характеристик системы.

Критерий Михайлова основан на исследовании характеристической функции D(jω) = U(ω) + jV(ω), полученной из характеристического многочлена подстановкой s = jω.

Основная формулировка: система n-го порядка устойчива, если кривая Михайлова, начинаясь при w=0 на действительной положительной полуоси, проходит при изменении частоты w от нуля до плюс бесконечности последовательно против часовой стрелки n квадрантов комплексной плоскости.

Дополнительная формулировка (следствие или форма 2): система n-го порядка устойчива, если четная U(w) и нечетная V(w) функции при изменении частоты w от нуля до плюс бесконечности обращаются в нуль поочередно n раз, начиная с нечетной функции, т.е. их корни перемежаются. Для построения графика используется та же таблица частот, что и в основной форме.

Указания к работе

Предварительно следует найти главную передаточную функцию системы (рисунок 1) W_yr(s) по выходу y относительно входа r с учетом параметров блоков 5 и 6 – сначала в общем виде, затем с численными значениями данных по своему варианту (значение коэффициента обратной связи k _ос принять равным единице).

Используя программу MICHCHAR "Критерий Михайлова" из библиотеки LinCAD и характеристическое уравнение системы (знаменатель передаточной функции), необходимо получить кривую Михайлова на комплексной плоскости (рисунок 5) с таблицей частот, соответствующих пересечениям кривой с осями координат и крайним точкам кривой по каждой оси. Кривая Михайлова представляет собой раскручивающуюся спираль, уходящую в бесконечность. Поэтому диапазон частот следует подобрать экспериментально, от нуля до значения частоты, при котором кривая последний раз пересекает какую-либо ось, для более точного определения координат пересечения действительной и мнимой осей и желаемого вида кривой Михайлова.

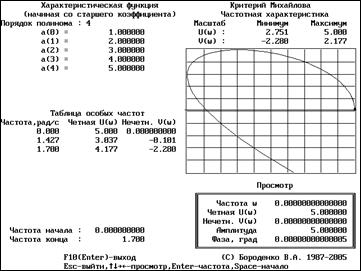
Рисунок 5

Таблица особых частот включает только минимум точек, поэтому, пользуясь перемещающимся маркером, желательно определить координаты точек, соответствующих наибольшим отклонениям по действительной или мнимой оси, и добавить их в таблицу. По расширенной таблице нужно построить кривую Михайлова в произвольном масштабе, по ее виду дать заключение об устойчивости системы. Если какой-либо оси не оказалось на графике, ее следует дорисовать приближенно, а на кривой поставить стрелку в сторону увеличения частоты.

Самостоятельно, используя полученную таблицу частот, построить графики четной U(ω) и нечетной V(ω) функций в соответ­ствии со второй формой (следствием) критерия Михайлова, проверить сделанный ранее вывод об устойчивости системы. На всех графиках обязательно указывать порядок системы (полинома) n.

3.4 Методический пример

Характеристическое уравнение САР

D(s) = s⁴ + 2s³ + 3s² + 4s + 5 = 0.

Расширенная таблица частот

ω, рад/с	U(ω)	V(ω)
0.000	5.000	0.000
0.800	3.490	2.176
1.230	2.750	1.198
1.427	3.037	-0.101
1.700	4.177	-2.280

Годограф характеристической функции D(jω)

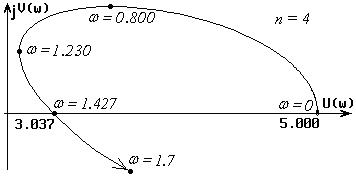
Система неустойчива, поскольку кривая Михайлова, начинаясь на положительной действительной оси, не проходит последовательно против часовой стрелки n квадрантов комплексной плоскости, где n=4 – порядок системы.

Графики четной и нечетной функций

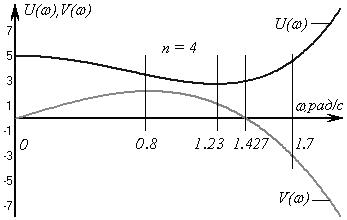
Система неустойчива, поскольку графики четной U(ω) и нечетной V(ω) функций, начинаясь с V(ω) = 0, не пересекают при возрастании частоты ось частот поочередно (число пересечений меньше n).

Содержание отчета

Отчет по лабораторной работе должен содержать название, цель работы, главную передаточную функцию системы в общем виде и после подстановки численных значений, характеристическое уравнение системы, полученные на ЭВМ таблицу частот и кривую Михайлова, построенный самостоятельно график четной и нечетной функций с заключением об устойчивости системы. На всех графиках должны быть указаны значения параметров в точках пересечения кривых с осями координат, порядок системы, обозначены оси и каждая кривая при количестве характеристик более одной.

К защите знать физический и математический признаки устойчивости систем, названия основных критериев устойчивости, формулировку критерия Михайлова и его следствия, методику построения кривой Михайлова вручную.

4 Выбор параметров регулятора методом D-разбиения

Цель работы

Целью работы является изучение методов проектирования систем с достижением заданных параметров устойчивости, в частности, метода D-разбиения по двум параметрам.

Общие сведения

Метод используется при синтезе систем для определения допус­тимых по условиям устойчивости пределов изменения некоторых па­раметров системы – обычно коэффициента усиления k или постоян­ной времени T регулятора.

Процесс построения в пространстве параметров системы об­ластей с разным числом правых корней характеристического урав­нения называется D-разбиением.

Областью устойчивости D(0) называют область в пространстве изменяемых параметров, каждой точке которой соответствуют только левые корни характеристического уравнения. Остальные D-области отличаются числом правых корней характеристического уравнения и обозначаются соответственно D(1) – область с одним правым полю­сом, D(2) – с двумя и т.д.

Граница любой D-области является отображением мнимой оси плоскости корней, она соответствует совокупности значений парамет­ров, при которых хотя бы один корень характеристического уравне­ния системы находится на мнимой оси.

Если система в пространстве всех своих параметров не имеет области устойчивости, она является структурно неустойчивой. На практике используют D-разбиение по одному параметру (результатом является отрезок на условной плоскости) и по двум параметрам (ре­зультатом является плоскость).

В случае D-разбиения по одному параметру все построения производят, изменяя значения одного параметра при постоянстве остальных. Чтобы получить плоскость, вещественный параметр искусственно делают двумерным, заменяя s = jw с образованием мнимой оси, однако окончательным результатом является отрезок на действительной оси.

Подставив s = jw в характеристическое уравнение системы, раз­решают его относительно изменяемого параметра, находят четную (действительную) U(w) и нечетную (мнимую) V(w) функции. Изменяя частоту w от 0 до плюс бесконечности, строят кривую D-разбиения и ее зеркальное отображение относительно действительной оси. Двига­ясь по кривой от точки w = -¥ до точки w = +¥ , наносят штриховку слева от кривой. (Напомним, что кривая D-разбиения является ото­бражением мнимой оси, а при движении по этой оси от -j¥ к +j¥ об­ласть устойчивости на плоскости корней располагается слева).

Направление штриховки указывает на область с наибольшим числом левых корней. При каждом переходе через кривую навстречу штриховке один корень характеристического уравнения становится правым, в обратном направлении – левым. Выбранную область-пре­тендент D(0) проверяют на устойчивость с помощью любого крите­рия, подставив значение параметра из этой области в характеристиче­ское уравнение. Поскольку изменяемый параметр является действи­тельной величиной, его допустимые значения лежат на отрезке дейст­вительной оси, заключенном внутри области устойчивости D(0).

Критическим называется значение параметра системы или коэффициента характеристического уравнения, при котором система находится на границе устойчивости.

Для проверки области-претендента на устойчивость системы четвертого порядка удобен критерий Гурвица, у которого должны выполняться два условия: необходимое – все коэффициенты характеристического уравнения положительны, и достаточное – определитель третьего порядка D₃ = a₃D₂ – a₁²a₄ = a₃·(a₁×a₂ - a₀×a₃) – a₁²a₄ > 0.

Указания к работе

В работе производится выбор значения коэффициента усиления k₁ регулятора, вошедшего в коэффициент характеристического уравнения a_n, по условию устойчивости системы при номинальных значениях остальных коэффициентов.

Предварительно следует выразить аналитически зависимость коэффициента характеристического уравнения a_n от коэффициента k₁.

Используя программу DRAZBTWO "D-разбиение по двум параметрам" из библиотеки LinCAD и характеристическое уравнение системы из предыдущей работы, получить на плоскости параметров область устойчивости при изменении в заданном диапазоне коэффициента a_n и одного из коэффициентов a₁ - a_n-1, оставив номинальными значения остальных коэффициентов. Какой из коэффициентов a₁ - a_n-1 лучше выбрать для изменения, подбирают экспериментально по наиболее характерному проявлению областей устойчивости, при этом его значение рекомендуется задавать в пределах 0.9-1.1 номинального.

На линии, соответствующей номинальному значению неосновного коэффициента a₁ - a_n-1, определить критическое значение a_{n, кр} , соответствующее пересечению границы области устойчивости, а в самой области устойчивости выбирается желаемое значение a_n приблизительно равноудаленным от границ области (рисунок 6).

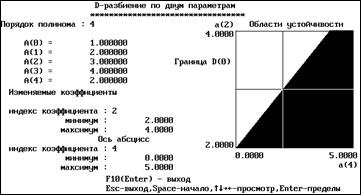
Рисунок 6

Самостоятельно оценить устойчивость системы по критерию Гурвица после подстановки выбранного значения a_n в характеристическое уравнение. Если устойчивость системы обеспечивается, по выбранной величине a_n найти значение k₁, которое должно использоваться во всех последующих работах взамен первоначально заданного. При нулевом значении k₁ следует немного изменить выбранное значение a_n.

4.4 Методический пример

Характеристическое уравнение системы

D(s) = a₀ s⁴ + a₁s³ + a₂ s² + a₃ s + a₄= s⁴ + 2s³ + 3s² + 4s + 2 = 0

Области устойчивости в пространстве коэффициентов 2 < a₂ < 4 и 0 < a₄ < 5

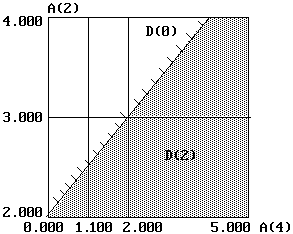
При номинальной величине a₂ = 3 критическое значение a_{4, кр1} = 0 в сторону уменьшения и a_{4, кр2} = 2 в сторону увеличения, оптимальное значение по устойчивости выбираем равным a₄ = 1.1.

Для проверки области-претендента на устойчивость по критерию Гурвица подставляем выбранное значение в характеристическое уравнение:

- характеристическое уравнение D(s) = s⁴ + 2s³ + 3s² + 4s + 1.1 = 0;

- условие D₃ = a₃·(a₁×a₂ - a₀×a₃) – a₁²a₄ = 8 – 4.4 =∙3.6 > 0 выполняется.

Принимая значение a₄ = 1.1, находим необходимое значение коэффициента k₁ = (a₄ – 1)/k₂/k₃ = (1.1 – 1)/(0.1∙10) = 0.1.

Рассчитанная с новым значением k₁ передаточная функция САР

.

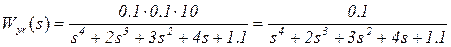Содержание отчета

Отчет по лабораторной работе должен содержать цель работы, характеристическое уравнение системы D(s) = 0, полученный на ЭВМ график областей D-разбиения с обозначением величин и масштаба по обеим осям, обозначением областей D( ) и штриховкой в сторону области устойчивости, визир с координатами выбранной точки, критическое значение a_{n, кр}, выбранное значение a_n, проверку устойчивости системы при этом значении по критерию Гурвица, зависимость a_n от коэффициента k₁, рассчитанное значение k₁ и вид передаточной функции системы после подстановки k₁.

К защите знать основные определения метода D-разбиения по одному параметру, порядок построения кривых, штриховки, выбора параметра, формулировки и порядок применения критериев Гурвица и Рауса, определение для критического параметра.

Цель работы

Целью работы является изучение методов проектирования систем по корням характеристического уравнения при заданных показателях качества регулирования.

Общие сведения

Корневые оценки учитывают влияние на вид переходного про­цесса положения полюсов и нулей системы на комплексной плоско­сти. Качество регулирования оценивают лишь для устойчивых систем.

Корни, ближайшие к мнимой оси, назы­вают доминирующими, если влиянием осталь­ных корней можно пренебречь (остальные кор­ни находятся в 5-10 раз дальше от мнимой оси).

Расстояние от мнимой оси до ближайше­го к ней корня характеристического уравнения (пары комплексных сопряженных корней) называется степенью устойчивости α_min или η, оно характеризует быстродействие системы. Максимальное по модулю отношение мнимой части корня к действительной из имеющихся полюсов называется степенью колебательности системы.

К основным показателям качества регулирования относятся время регулирования или установления (длительность процесса) и перерегулирование (размах качаний при переходном процессе). Для оценки времени регулирования t_рег находят сначала степень устойчивости системы α_min или η, откуда при ошибке ∆ = 5 %

.

Для оценки перерегулирования s определяют степень колеба­тельности μ системы, а затем значение перерегулирования . При нескольких парах комплексных корней максимальное значение μ у того корня, который первым встречается лучу, проведенному из начала координат по положительной мнимой полуоси и поворачиваемому против часовой стрелки. При единственной паре комплексных корней необходимость выбора отпадает.

Совокупность траекторий, описываемых на комплексной плос­кости корнями характеристического уравнения замкнутой системы при изменении одного из ее параметров от 0 до ∞, называется корне­вым годографом.

Поскольку обычно делают оценку для замкнутой системы, то в ее характеристическое уравнение попадают и нули, и полюса разомк­нутой системы. Если , то . Ча­ще всего изменяют k – коэффициент усиления регулятора, вычисляют для каждого значения корни и наносят их на комплексную плоскость.

При построении корневого годографа обычно используют или учитывают его свойства:

- число ветвей корневого годографа равно степени характеристиче­ского уравнения;

- ветви комплексных частей корневого годографа симметричны отно­сительно действительной оси;

- точки расхождения ветвей на действительной оси соответствуют кратным действительным корням характеристического уравнения;

- при k, стремящемся к нулю, траектории корней начинаются в полю­сах передаточной функции разомкнутой системы;

- при k, стремящемся к бесконечности, m траекторий корней заканчи­ваются в нулях передаточной функции разомкнутой системы, а ос­тальные n-m ветвей асимптотически уходят в бесконечность. Здесь m – это порядок полинома числителя, а n – порядок полинома знамена­теля передаточной функции системы.

Указания к работе

В работе производится выбор значения коэффициента обратной связи k_ос в звене 6, ранее принимаемого равным единице, по условию получения минимального времени регулирования.

Поскольку этот коэффициент попадает в свободный член характеристического уравнения a_n, предварительно следует выразить аналитически зависимость этого коэффициента от коэффициента k_ос, учитывая новое значение k₁, полученное в предыдущей работе.

Используя программу ROOTLOCS "Корневой годограф" из библиотеки LinCAD и характеристическое уравнение системы из предыдущей работы, получить корневой годограф системы (рисунок 7) при изменении коэффициента a_n в задаваемом диапазоне (от нуля до значения, при котором корни перемещаются вправо от мнимой оси). Перемещая маркер по годографу, найти значение коэффициента, при котором все корни максимально удалены от мнимой оси. При этом и будет обеспечиваться наименьшее возможное время регулирования (наибольшее значение степени устойчивости).

Перенести корневой годограф в отчет с обозначением осей и масштаба, показать стрелками на ветвях направления движения корней при увеличении a_n, провести линию степени устойчивости и луч выбора корней для оценки степени колебательности. Возле точек, соответствующих наименьшему, наибольшему и выбранному значениям коэффициента a_n подписать значения этого коэффициента. Допускается полюс, далеко отстоящий от мнимой оси, не показывать, если это не нарушает наглядности выбора показателей качества.

Рисунок 7

Для выбранного значения a_n записать соответствующие ему величины времени регулирования t_рег, перерегулирования s и полученное значение коэффициента обратной связи k_ос.

5.4 Методический пример

Характеристическое уравнение системы

D(s) = s⁴+2s³+3s²+4s+(k₁k₂k₃k_oc+1) = s⁴ + 2s³ + 3s² + 4s + 1.1 = 0.

Принимаем диапазон изменения коэффициента a₄, включающего коэффициент обратной связи, в пределах граничных значений 0-2, найденных в предыдущей работе.

Таблица значений корней знаменателя ПФ

	Значение коэффициента а4
а4, min = 0.000	а4, max = 2.000	а4, опт = 0.523
полюса системы	0.000	-1.000	-0.145
-0.174 + j1.547	-1.000	-0.140 + j1.506
-0.174 - j1.547	0.000 + j1.414	-0.140 - j1.506
-1.650	0.000 - j1.414	-1.574

Корневой годограф

Пока<