Tf-, zpk-, ss- формы для заданной передаточной функции
Глава 1
Математическое описание линейных систем
Tf-, zpk-, ss- формы для заданной передаточной функции
tf – полиномиальная форма, в которой передаточная функция задается двумя векторами-строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней S.
Результаты в MATLAB:
>>W= tf ([1260 2520 0], [1 16 81 126]);
Transfer function:
12620s^2+2520s
---------------------------------
s^3 + 16s^2 + 81s + 26
zpk - форма нулей, полюсов и коэффициента усиления, в которой полиномы записаны через нули числителя – zi и полюса знаменателя pj.
Результаты в MAT-LAB:
>>zpk(W)
Zero/pole/gain:
1260 s (s+2)
----------------------
(s+7) (s+6) (s+3)
ss - форма представляет передаточную функцию в параметрах пространства состояний. Система n-го порядка с одним входом и одним выходом в параметрах пространства состояний описывается системой уравнений:
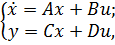
где А - матрица коэффициентов обратных связей, охватывающих все n интеграторов; B - матрица коэффициентов связей входов всех интеграторов с входом модели; C - матрица коэффициентов связей выходов всех интеграторов с выходом модели; D - матрица коэффициентов связей входов и выходов модели напрямую, минуя интеграторы.
Результаты в MATLAB:
>>ss(W)
a =
x1 x2 x3
x1 -16 -10.13 -3.938
x2 8 0 0
x3 0 4 0
b =
u1
x1 32
x2 0
x3 0
c =
x1 x2 x3
y1 39.38 9.844 0
d =
u1
y1 0
Временные характеристики системы в пакете MATLAB
| h(t) |
h(t ) >> step(W)
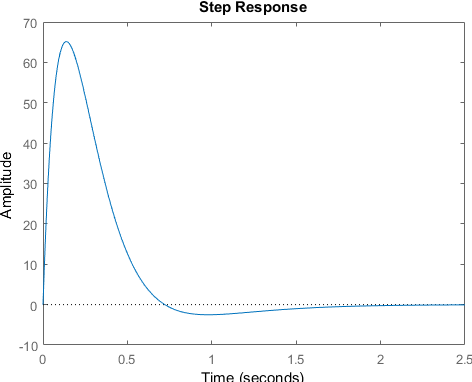
| t |
Рисунок 1.1 – Переходная характеристика h(t)
| w(t) |
Impulse Response
| t |
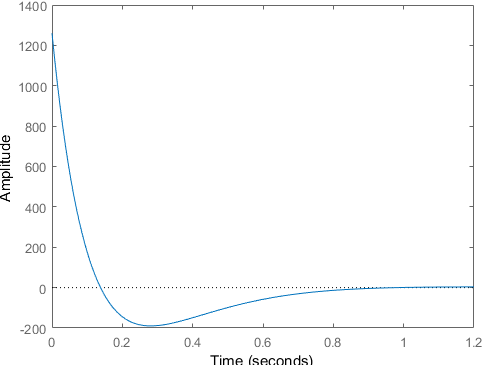
Рисунок 1.2 – Импульсная переходная характеристика w(t)
Значения выходных сигналов временных характеристик становятся равными коэффициенту усиления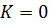 
. Полученные графики подтверждают расчетные данные.
Частотные характеристики в пакете MATLAB
>>bode(W)
| ω ) |
| L(ω) ) |
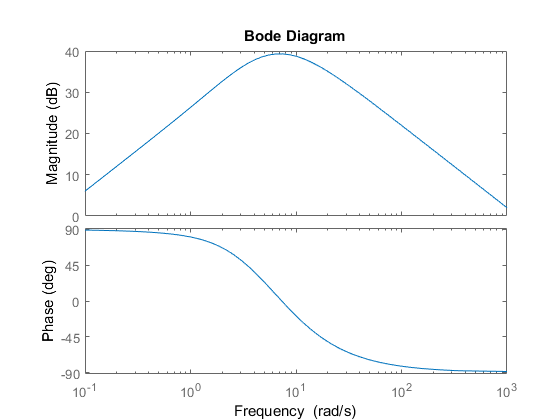
Рисунок 1.5 – ЛАЧХ и ЛФЧХ системы
Асимптотические ЛАЧХ и ЛФЧХ приведенные в приложении 1 совпадают с характеристиками построенными в пакете MATLAB. Следовательно, частотные характеристики построены верно.
Амплитудно-фазовая частотная характеристика (АФЧХ) — удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. На таком графике частота выступает в качестве параметра кривой, фаза и амплитуда системы на заданной частоте представляется углом и длиной радиус-вектора каждой точки характеристики.
>> nyquist(W)
| P(ω) |
| Q(ω) |
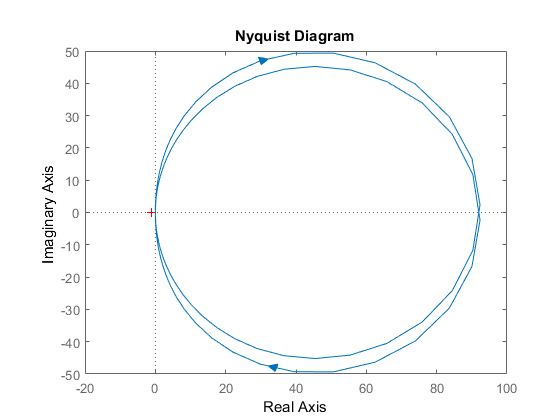
Рисунок 1.6 – АФЧХ системы
Глава 1
Математическое описание линейных систем
tf-, zpk-, ss- формы для заданной передаточной функции
tf – полиномиальная форма, в которой передаточная функция задается двумя векторами-строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней S.
Результаты в MATLAB:
>>W= tf ([1260 2520 0], [1 16 81 126]);
Transfer function:
12620s^2+2520s
---------------------------------
s^3 + 16s^2 + 81s + 26
zpk - форма нулей, полюсов и коэффициента усиления, в которой полиномы записаны через нули числителя – zi и полюса знаменателя pj.
Результаты в MAT-LAB:
>>zpk(W)
Zero/pole/gain:
1260 s (s+2)
----------------------
(s+7) (s+6) (s+3)
ss - форма представляет передаточную функцию в параметрах пространства состояний. Система n-го порядка с одним входом и одним выходом в параметрах пространства состояний описывается системой уравнений:
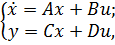
где А - матрица коэффициентов обратных связей, охватывающих все n интеграторов; B - матрица коэффициентов связей входов всех интеграторов с входом модели; C - матрица коэффициентов связей выходов всех интеграторов с выходом модели; D - матрица коэффициентов связей входов и выходов модели напрямую, минуя интеграторы.
Результаты в MATLAB:
>>ss(W)
a =
x1 x2 x3
x1 -16 -10.13 -3.938
x2 8 0 0
x3 0 4 0
b =
u1
x1 32
x2 0
x3 0
c =
x1 x2 x3
y1 39.38 9.844 0
d =
u1
y1 0