Раздел 1. Основы теоретической механики
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКРАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ ПГУПС
МЕТОДИЧЕСКОЕ ПОСОБИЕ
по практическим и лабораторным занятиям
по дисциплине
ТЕХНИЧЕСКАЯ МЕХАНИКА
для специальности
08.02.10. Строительство железных дорог, путь и путевое хозяйство
Преподаватель Яковцева Галина Борисовна
Птрозаводск
СОДЕРЖАНИЕ
Предисловие…………………………………………………………………………….3
Перечень практических занятий……………………………………. …………….3-5
Практическая 1. Решение задач на равновесие сил в аналитической форме…….6-9
Практическая2. Определение главного вектора и главного момента произвольной плоской системы сил…………………………………………………………………9-12
Практическая3. Определение реакций в опорах балочных систем с проверкой
Правильности решения…………………………………………………………………… 12-18
Практическая 4. Выполнение расчетов на прочность при растяжении
и сжатии …………………………………………………………………………….18-23
Практическая5. Определение диаметра вала из условия прочности при кручении......................................................................................................................24-29
Практическая6. Построение эпюр поперечных сил и изгибающих
моментов.……………………....................................................................................30-35
Практическая7. Выполнение расчетов на жесткость при изгибе……….. …...35-41
Практическая 8. Выполнение расчета прямозубых передач и определение параметров зубчатых колес……………………………………………………………………..41-49
Практическая 9. Подбор подшипников качения по динамической
грузоподъемности…………………………………………………………………..50-55
Перечень лабораторных занятий……………………………………………………56
Подготовка студентов к проведению лабораторных занятий…………………..56-57
Лабораторное занятие 1. Определение центра тяжести плоских фигур…………………………………………………………………………… …..58-60
Лабораторное занятие 2. Проведение испытаний на растяжение образца из низкоуглеродистой стали………………………………………………………….60-65
Лабораторное занятие 3. Определение максимального вращающего момента по мощности на валу………………………………………………………………….65-70 Приложение………………………………………………………………………..70-73 Литература…………………………………………………………………………….74
ПРЕДИСЛОВИЕ
Предлагаемое вниманию методическое пособие по поведению практических занятий полностью соответствует действующей программе курса по дисциплине «Техническая механика» специальности:
08.02.10. Строительство железных дорог, путь и путевое хозяйство
Целью выполнения практических занятий является:
- научиться решать типовые задачи;
- получить навыки правильного использования расчетных формул;
- установить взаимосвязь между теорией и практикой;
- закрепить знания по темам.
В методических указаниях к практическим занятиям приводятся:
- цели,
- краткое теоретическое обоснование,
- методики выполнения работ,
- примеры решения задач,
- задания,
- отчет о работе,
Перечень практических занятий:
Раздел 1. Основы теоретической механики
Тема 1.2. Плоская система сходящихся сил
Практическое занятие 1. Определение реакций в связях аналитическим, графическим и графоаналитическим способами.
Практическое занятие 2.Определение реакций в опорах балочных систем
Раздел 2. Сопротивление материалов
Тема 2.2. Растяжение и сжатие
Практическое занятие 3. Расчет на прочность при растяжении и сжатии.
Тема 2.3Срез и смятие.
Практическое занятие 4. Расчет на прочность при срезе и смятии
Тема 2.4. Сдвиг и кручение
Практическое занятие 5. Расчет прочность при кручении.
Тема 2.5. Изгиб
Практическое занятие 6. Построение эпюр поперечных сил и изгибающих моментов. Выполнение расчетов на жесткость при изгибе.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 1
Практическое занятие 1
Определение реакций в связях аналитическим, графическим и графоаналитическим способами
К выполнению задания необходимо приступить после изучения темы 1.2. «Плоская система сходящихся сил».
Цель:научиться определять реакции в связях системы сил;
- приобрести умения в решении задач на равновесие системы сил для тел с идеальными связями всех видов и всеми видами нагрузок, кроме распределенных моментов;
- научиться выбирать в ходе решений задач рациональное направление координатных осей, выполнять проверку правильности решений;
- освоить методику решения задач на равновесие плоской системы сил;
Краткие теоретические сведения
АЛГОРИТМ ВЫПОЛНЕНИЯ
Выполняем проверку решения
Аналитическим ,графическим или геометрическим способом.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 2
Практическое занятие 2
Свойства пар
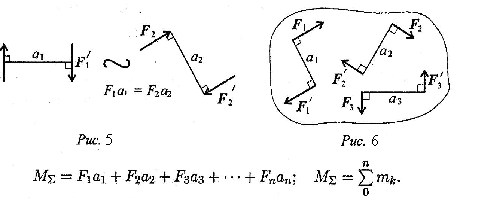
1. Пару сил можно перемещать в плоскости ее действия.
2. Эквивалентность пар. Две пары, моменты которых равны,
(рис. 5) эквивалентны (действие их на тело аналогично).
3. Сложение пар сил. Систему пар сил можно заменить равнодействующей парой. Момент равнодействующей пары равен алгебраической сумме моментов пар,
составляющих систему (рис. 6)
4. Равновесие пар.
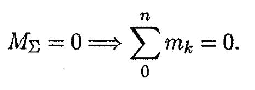 Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю
Балочные системы
уравнений во второй форме:
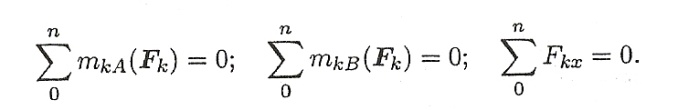
Составляются уравнения моментов относительно точек крепления балки. Поскольку момент силы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
| 20 кН |
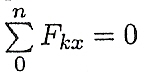
Из уравнения определяется реакция Rвх
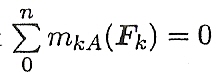
Из уравнения определяется реакция Нву
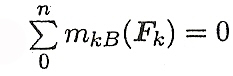
Из уравнения определяется реакция Rav
Для контроля правильности решения используется дополнительное уравнение
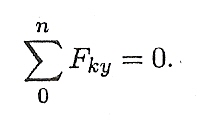
При равновесии твердого тела, где можно выбрать три точки, не лежащие на одной прямой, удобно использовать систему уравнений в третьей форме (рис. 6.6):
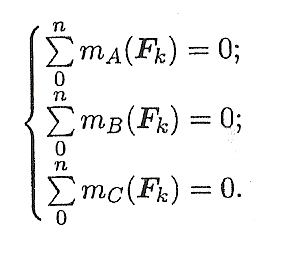
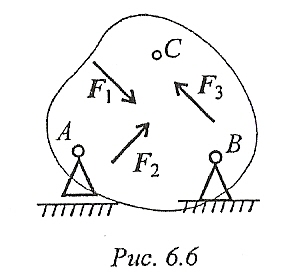
АЛГОРИТМ ВЫПОЛНЕНИЯ
1. Заменяют распределённую нагрузку её равнодействующей
Для равномерно распределённой нагрузки равнодействующая равна произведению интенсивности нагрузки g на длину участка ℓ , на котором она действует G = gℓ
Перед решением задач рекомендуется уяснить и закрепить порядок нахождения равнодействующей и определения расстояний от неё до опор. При отсутствии навыков решения таких задач необходимо указывать положение равнодействующей относительно опор.
2. Обозначают опоры
Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно – неподвижную и вторую шарнирно –подвижную опору.
Расчётная схема
RА Rв М
А В
G1 F G2
1 м 1,25м 2,25 м 1 м 1,5 м 1,5 м
Решение: 1. Заменяем распределённую нагрузку равнодействующей.На балку действуют нагрузки разной интенсивности, поэтому для каждой из них найдём равнодействующую.
G1 = g1 · 20 (1+3,5) = 90 кН, G2 = g2 · 15 (1,5+1,5) = 45 кН
2 Обозначим опоры А и В, Укажем опорные реакцииRА, Rв
3. Составляем уравнения равновесия:ΣМА = 0 , ΣМВ = 0
ΣМА = 0: G1 · 1,25 - F · 4,5 + G2 · 6 - Rв · 6 – М = 0
Rв · 6 = - G1 · 1,25 + F · 4,5 - G2 · 6 + М
Rв = - G1 · 1,25 + F · 4,5 - G2 · 6 + М / 6
Rв = 90 · 1,25 – 30 · 4,5 +45 · 6 – 25 / 6, Rв = 37,1 кН.
ΣМВ = 0: -М + F · 1,5 - G1 · 4,75 + RА · 6 = 0
RА · 6 = М - F · 1,5 + G1 · 4,75
RА = М - F · 1,5 + G1 · 4,75 / 6
RА = 25 - 30 · 1,5 + 90 · 4,75 / 6 RА = 67,9 кН.
5.Выполняем проверку, используя уравнениеΣFy= 0, которое примет вид
RА - G 1 + F + Rв - G2 = 0; 67,9 – 90 +30 +37,1 – 45 = 0
45 – 45 = 0; 0 = 0, реакции опор определены правильно.
Ответ: RА = 67,9 кН., Rв = 37,1 кН.
Задание Определить величины реакций в опорах балочных систем под действием сосредоточенных сил и распределенной нагрузки. Провести проверку правильности решения. Данные взять из таблицы 2, схема 2 - одноопорной балки (заделка) и таблицы 3, схема 3– для двухопорной балки с шарнирными опорами
Таблица 2
| Исходные данные | вариант | |||||||||
| № схемы | ||||||||||
| Угол α0 | ||||||||||
| a1,м | 0,7 | 2,5 | 0,7 | 2,0 | 1,7 | 0,8 | 1,2 | 1,2 | 0,5 | |
| a2,м | 0,8 | 0,6 | 0,5 | 4,5 | 0,3 | 2,2 | 1,2 | 0,8 | 1,3 | |
| a3,м | 1,5 | 0,8 | 0,7 | 0,5 | - | 1,2 | 1,5 | 2,6 | 2,5 | 2,2 |
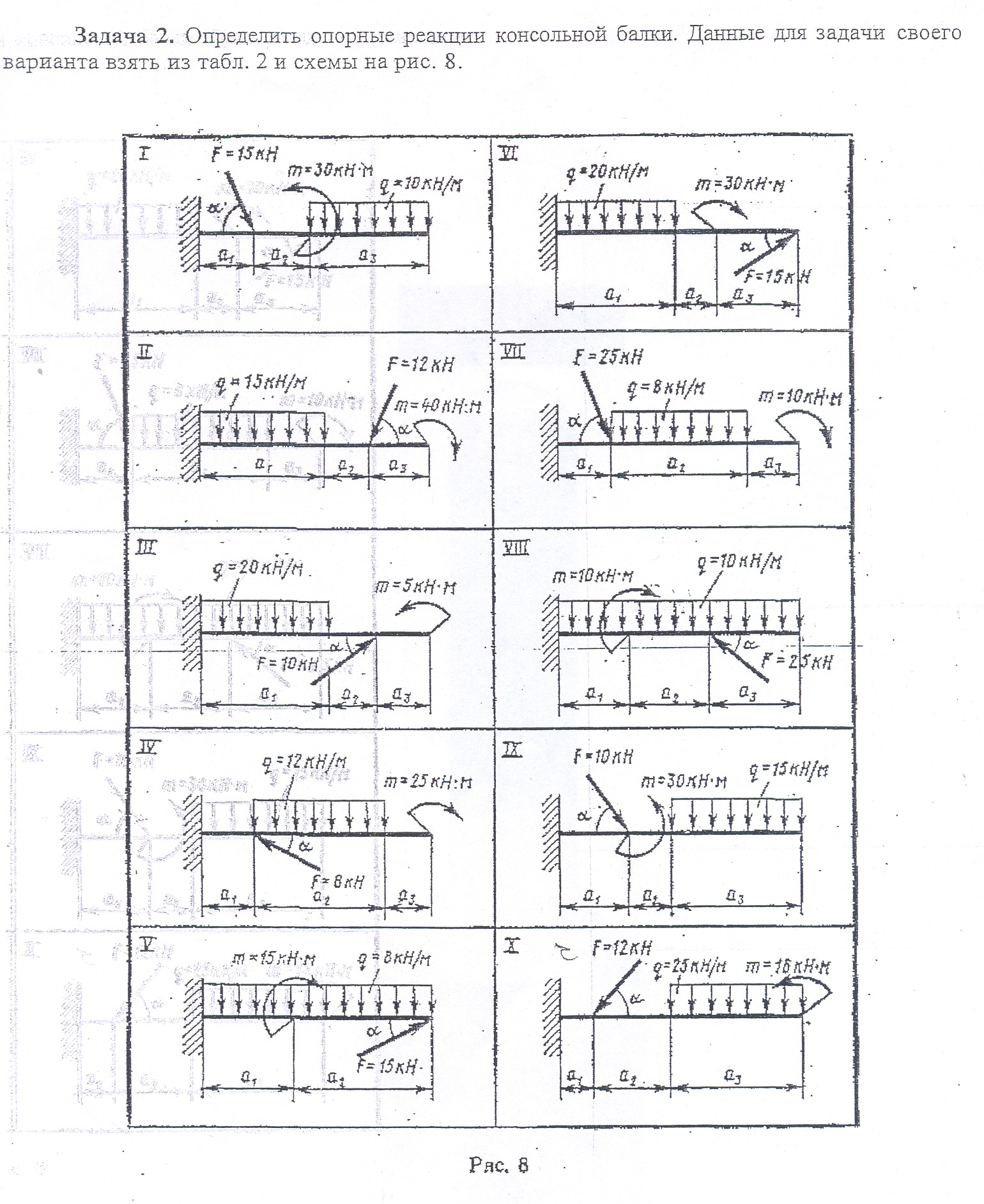 Схема 2
Схема 2
Таблица 3
| Исходные данные | вариант | |||||||||
| № схемы | ||||||||||
| Угол α0 | ||||||||||
| a1,м | 1,2 | 2,5 | 1,5 | 3,0 | 1,2 | 1,1 | 1,2 | 1,5 | 1,8 | 1,5 |
| a2,м | 0,5 | 1,2 | 1,2 | 0,8 | 1,5 | 2,5 | 3,0 | 2,5 | 2,2 | 0,8 |
| a3,м | 0,8 | 0,8 | 2,5 | 1,2 | 1,5 | 0,7 | 0,5 | 1,5 | 0,7 | 1,5 |
| а4,м | 2,5 | 1,2 | - | - | 0,5 | 0,7 | 0,8 | - | - | 0,6 |
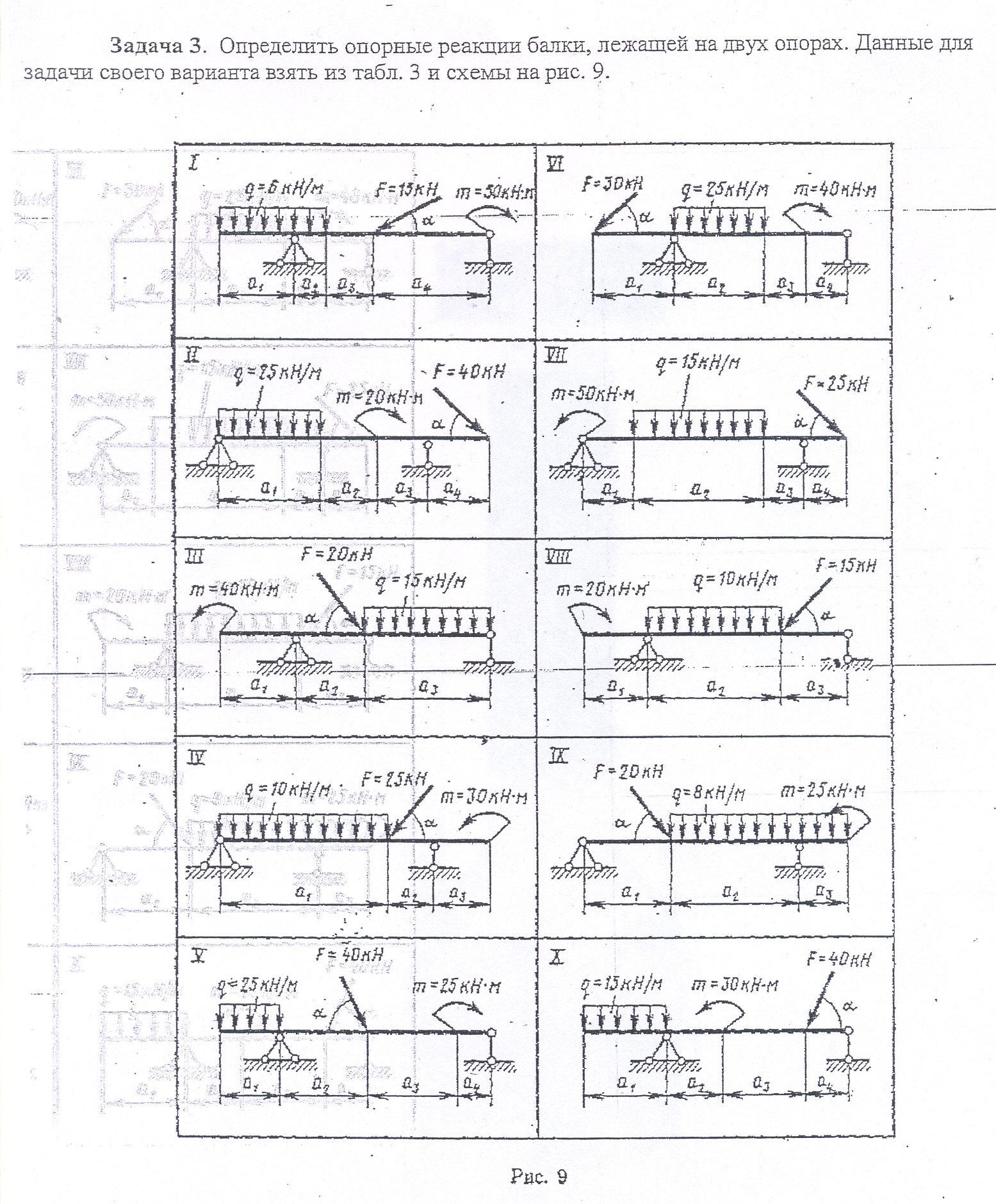 Схема 3
Схема 3
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
| Разраб. |
| Провер. |
| . |
| Лит. |
| Листов |
| Группа_____________________ |
Оборудование (приборы, материалы, дидактическое обеспечение)________________________________________________________
Компьютерная программа (если используется): Наименование программы_________________________________________________________
| Рисунок: | Дано: _____________________________________ _____________________________________ _____________________________________ Определить реакции в заделке: ____________________________________ _____________________________________ |
| Расчётная схема: | 1 Выбираем объект, равновесие которого рассматриваем: балка Обозначаем опору А 2 Заменяем распределённую нагрузку её равнодействующей G = gℓ (если такая нагрузка имеется ) G =____________ 3 Освобождаем от опор и заменяем их действие на балку реакциями. |
| 4 Проанализируем, полученную систему сил. 5Выбираем систему координат - проводим оси «Х» и «У» 6 Составляем уравнения равновесия вида: ΣFx ΣFх = 0 , ΣFу = 0, ΣМА = 0 |
Решение уравнений:
Выполняем проверку решения:Для этого составляют уравнение равновесияотносительно мнимой точки (В)
ΣМ(В)=0
Вывод:_____________________________________________________________
|
| Дано: _____________________________________ _____________________________________ _____________________________________ Определить реакции в опорах: ____________________________________ _____________________________________ | ||||||||
| Расчётная схема: | 1 Выбираем объект, равновесие которого рассматриваем: балка Обозначаем опорыА-В 2 Заменяем распределённую нагрузку её равнодействующей G = gℓ (если такая нагрузка имеется ) G=_____________________________ 3 Освобождаем балку от опор и заменяем действие на балку реакциями. | ||||||||
| 4 Проанализируем, полученную систему сил. 5Выбираем систему координат - проводим оси «Х» и «У» 6 Составляем уравнения равновесия вида: ΣFx = 0 ΣFу = 0 , ΣМА = 0, ΣМВ = 0 |
| Решение уравнений |
Выполняем проверку решения:Для этого составляют уравнение равновесия:
ΣFу = 0
Вывод:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
1.Что называется плечом пары?_____________________________________________
________________________________________________________________________
________________________________________________________________________
2.Чтобы определить эффект действия пары сил, надо знать?_____________________
________________________________________________________________________
3.Пару сил можно уравновесить…?__________________________________________
________________________________________________________________________
4.Зависит ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы? ________________________________________________________________________________________________________________________________________________
5.Для чего используется рычаг?____________________________________________
_______________________________________________________________________
6.Какую из форм уравнений равновесия целесообразно использовать при определении реакций в заделке?_____________________________________________
________________________________________________________________________
7.Когда момент силы относительно точки положителен?_______________________
_______________________________________________________________________
8. Какую из форм уравнений равновесия целесообразно использовать при определении реакций в опорах двухопорной балки и почему?_________________________________________________________________
________________________________________________________________________________________________________________________________________________
9.Что вызывает пара сил?________________________________________________
______________________________________________________________________
10. Можно ли перемещать пару сил в плоскости ее действия?_______________________________________________________________
________________________________________________________________________________________________________________________________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 3
Практическое занятие 3
АЛГОРИТМ ВЫПОЛНЕНИЯ
1.Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статистики (закону действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей.
3.Выбираем систему координат так, чтобы одна из осей координат совпала с неизвестной силой.
Решение
1. Определить нагрузку на стержни. Рассмотрим равновесие точки В, определим реакции стержней. По пятой аксиоме статистики (закону действия и противодействия) реакция стержня численно равна нагрузке на стержень.
Наносим реакции связей, действующих в точке В. Освобождаем точку В от связей (рис. П6.1).
Выбираем систему координат так, чтобы одна из осей координат совпала с неизвестной силой (рис. П6.1б).
Составим систему уравнений равновесия для точки В:
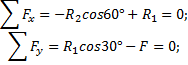
Решаем систему уравнений и определяем реакции стержней.
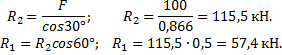
Направление реакций выбрано верно. Оба стержня сжаты. Нагрузки на стержни: F1 = 57,4 кН; F2 = 115,5 кН.
2. Определяем потребную площадь поперечного сечения стержней из условий прочности.
Условие прочности на сжатие: σ = N/А≤ [σ], откуда
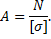
Стержень 1 (N1 = Аl):
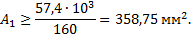
Для круга
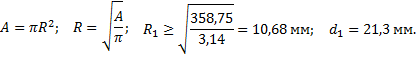
Стержень 2 (N2 = F2):
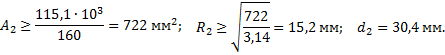
Полученные диаметры округляем: d1 = 25 мм, d2 = 32 мм.
3. Определяем удлинение стержней 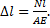
Укорочение стержня 1:
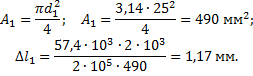
Укорочение стержня 2:
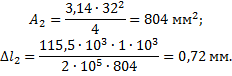
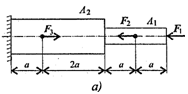
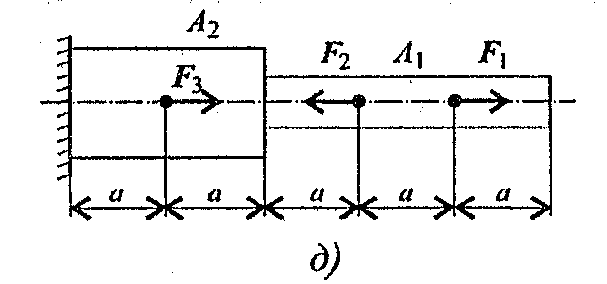
Задание 1. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брус нагружен силами F1, F2; F3. Площади поперечных сечений А1 и А2. Принять Е = 2.105 H/мм2.
Данные взять из таблицы 4, схема 4.
Таблица 4
| Параметр | Вариант | |||||||||
| F1, кН | ||||||||||
| F2, кН | ||||||||||
| F3, кН | ||||||||||
| A1, см | 1,8 | 1,6 | 1,0 | 2,0 | 1,2 | 0,9 | 1,9 | 2,8 | 2,1 | 1,9 |
| A2, см2 | 3,2 | 2,4 | 1,5 | 2,5 | 2,8 | 1,7 | 2,6 | 3,4 | 2,9 | 2,4 |
| a, м | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,4 | 0,3 | 0,2 | 0,5 | 0,6 |
Схема 4
 Вариант 1-5 Вариант 1-5 | Вариант 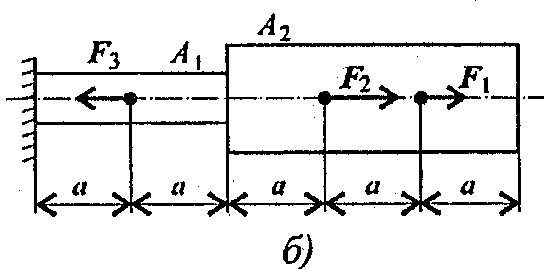 6-10 6-10 |
Вариант 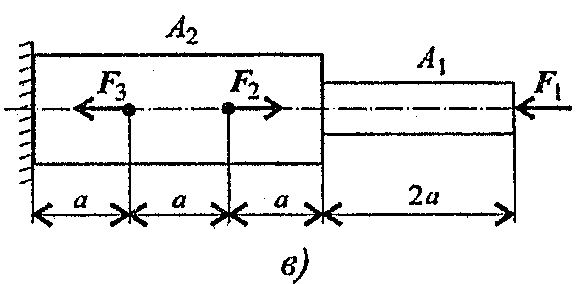 7-15 7-15 | Вариант 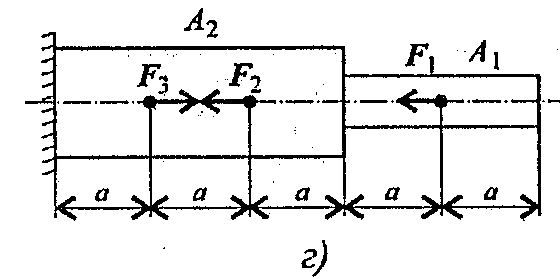 15-20 15-20 |
| Вариант 21-25 | 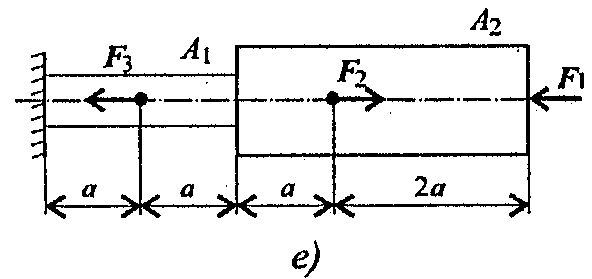 Вариант 25-30 Вариант 25-30 |
Задание 2. Балка АВ, на которую действуют указанные нагрузки, удерживается в равновесии тягой ВС. Определить размеры поперечного сечения тяги для двух случаев: 1) сечение - круг; 2) сечение - уголок равнополочный по ГОСТ 8509-86. Принять [σ] = 160 МПа. Собственный вес конструкции не учитывать. Данные взять из таблицы 5, схема 5.
Таблица 5
| Параметр | ||||||||||
| F, кН | ||||||||||
| m, кН.м | ||||||||||
| q, кН/м |
Схема 5
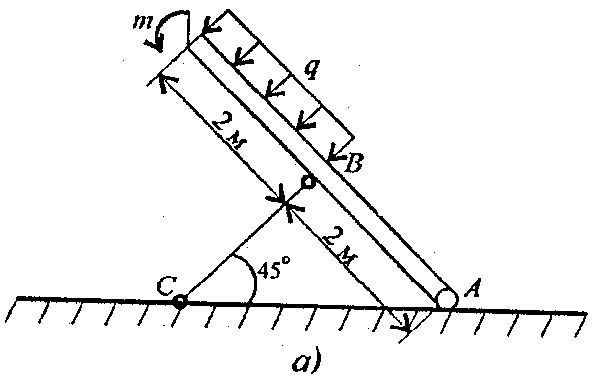 вариант 1 - 5 вариант 1 - 5 | 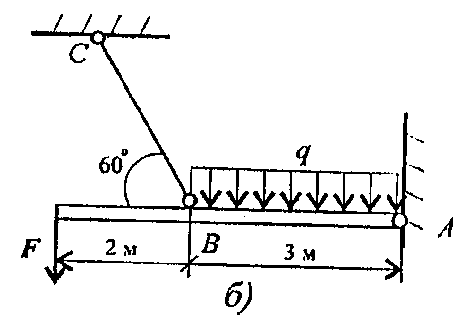 Вариант 6 - 10 Вариант 6 - 10 |
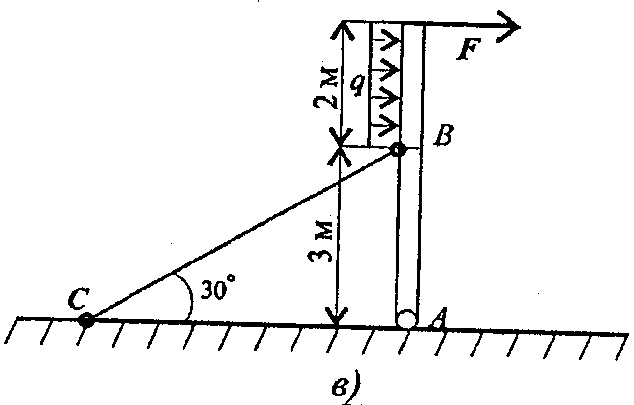 вариант 11 - 15 вариант 11 - 15 | 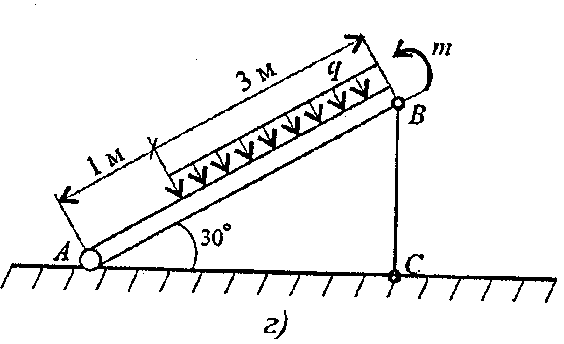 вариант 16- 20 вариант 16- 20 |
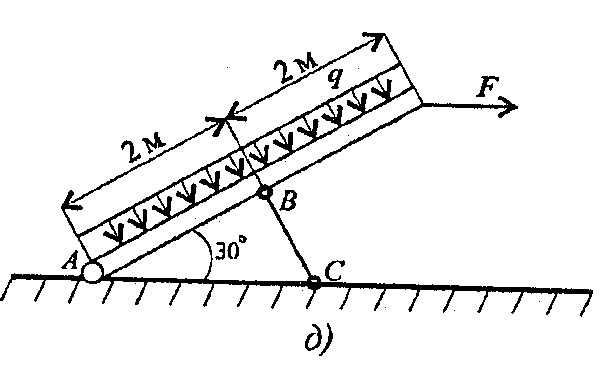 вариант 21 - 25 вариант 21 - 25 | 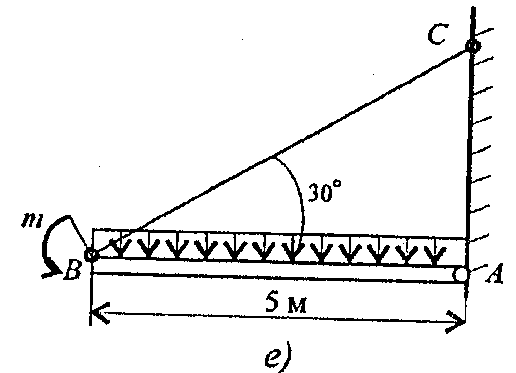 вариант 26 - 30 вариант 26 - 30 |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
| Разраб. |
| Провер. |
| Лит. |
| Листов |
Оборудование (приборы, материалы, дидактическое обеспечение)_________________________________________________________
Компьютерная программа (если используется): Наименование программы_______________________________________________________
Дано:_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Определить:_________________________________________________________
Решение:
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| ПЗ |
1. Что такое центральное растяжение и сжатие?_____________________________________
____________________________________________________________________________________________________________________________________________________________________________
2. Что понимается под продольной силой в брусе, и каким способом она определяется?___________________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________
3. Какое правило знаков принято при определении продольной силы? ____________________________________________________________________________________________________________________________________________________________________
4. Какова размерность продольной силы?___________________________________________
5. Как строится эпюра продольной силы и с какой целью? ______________________
______________________________________________________________________
_________________________________________________________________________________
6. Что такое эпюра продольной силы? ________________________________________
_______________________________________________________________________________________
7. Что такое напряжение? Чем определяется знак напряжения? __________________
________________________________________________________________________________________________________________________________________________________________________
8. Напишите условие прочности при растяжении или сжатии.____________________
________________________________________________________________________
9. Что называется абсолютной (полной) продольной деформацией? Напишите формулу абсолютной деформации._______________________________________________
_____________________________________________________________________________________________________________________________________________________________________
10. Как формулируется закон Гука? Напишите формулы, выражающие закон Гука, для относительной продольной деформации бруса._______________________________
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 4
Практическое занятие 4
Примеры деталей, работающих на сдвиг (срез) и смятие
1. Ось (рис. 23.5).
В случае, если толщина детали 2 меньше,
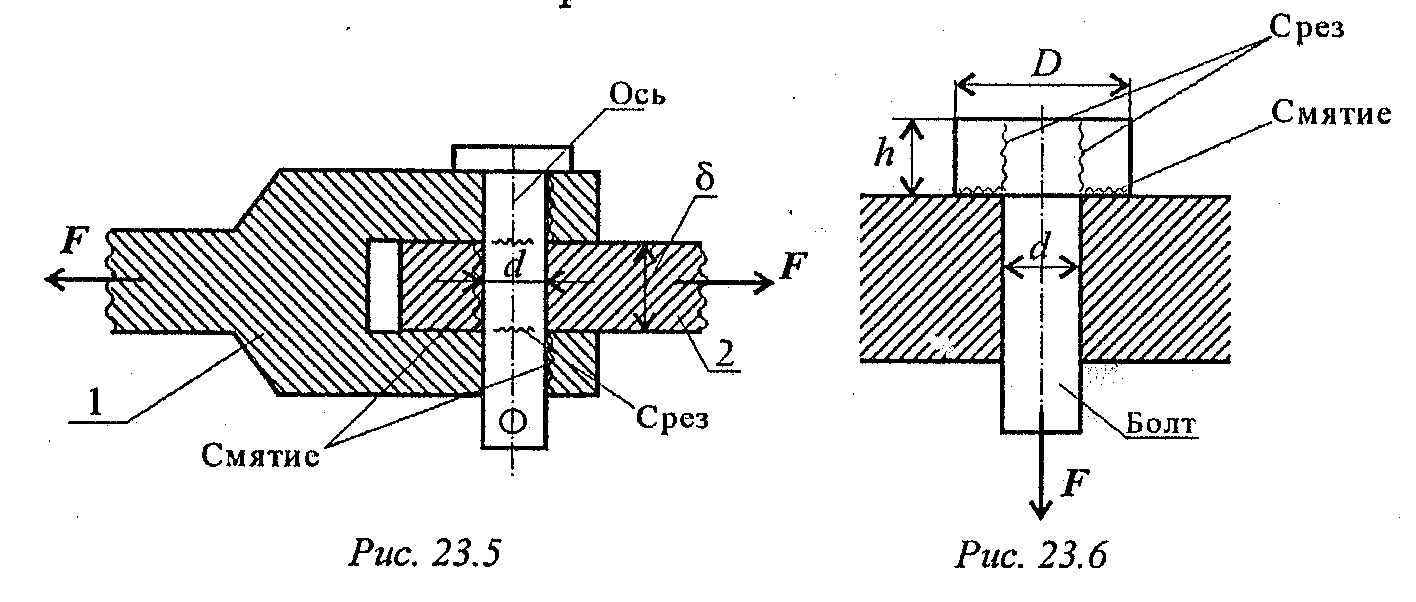
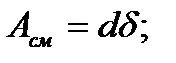
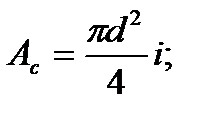
i = 2 - количество площадей среза.
2. Болт (рис. 23.6).
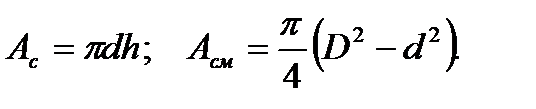
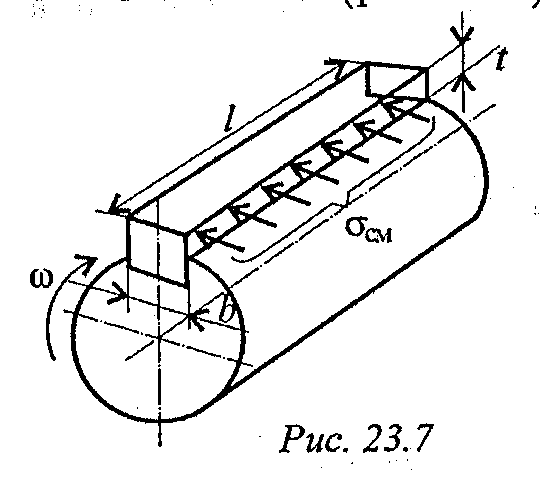 3. Шпонки (рис. ~3. 7) работают на срез и смятие, но рассчитываются только на смятие.
3. Шпонки (рис. ~3. 7) работают на срез и смятие, но рассчитываются только на смятие.
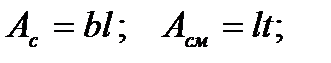 где l - длина шпонки; t - высота выступающей части; b - ширина шпонки.
где l - длина шпонки; t - высота выступающей части; b - ширина шпонки.
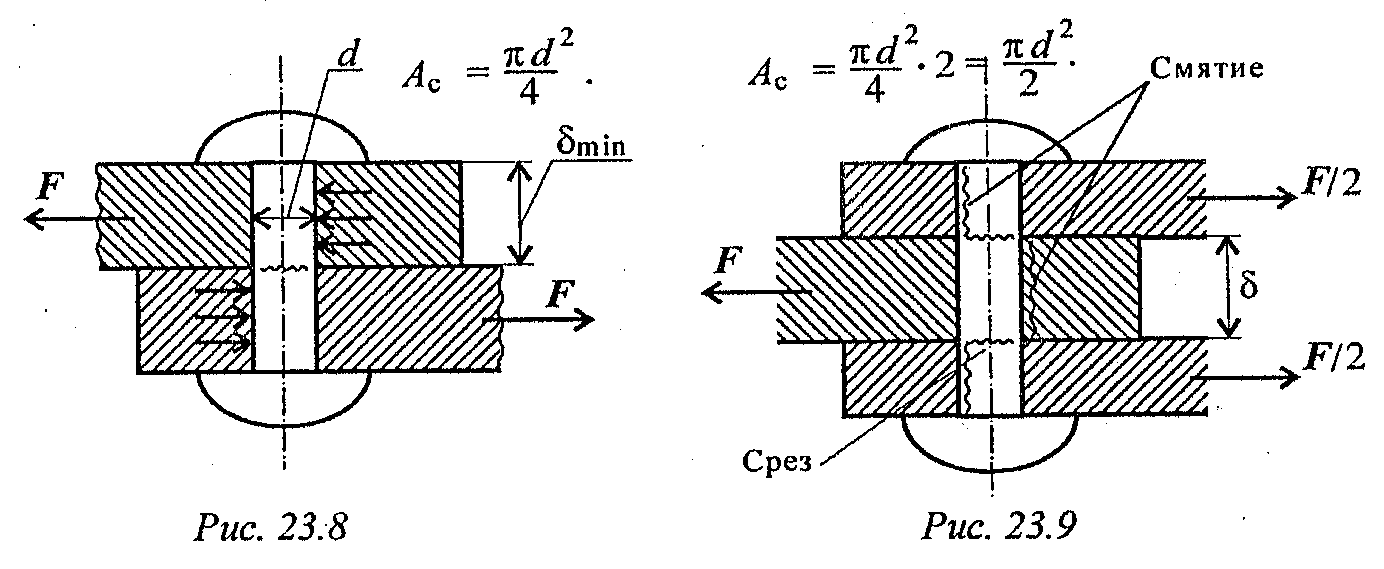
4. Заклепка односрезная (рис. 23.8), двухсрезная (рис. 23.9).
5. Сварное соединение (рис. 23.10).
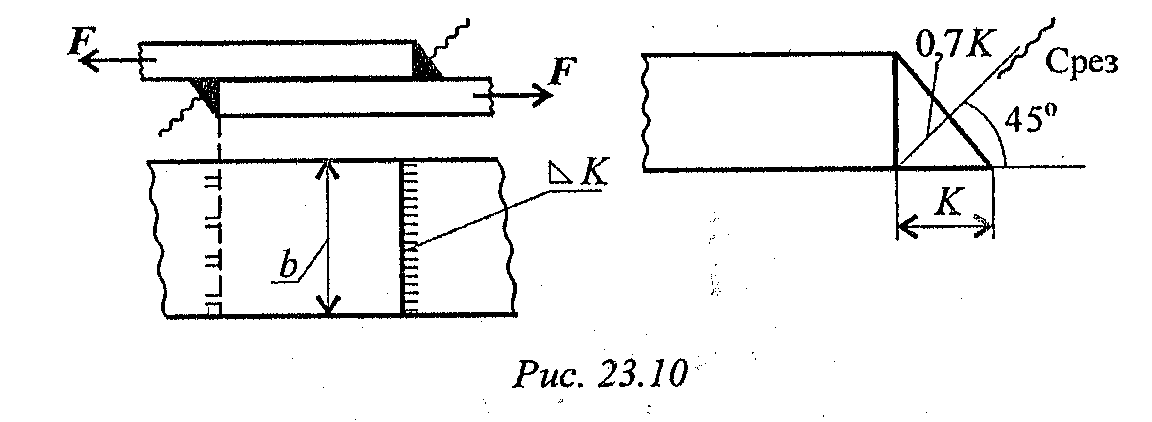
Угловой шов разрушается под углом 45о к плоскости разъема в результате среза. К - катет углового шва, подбирается по толщине свариваемого листа.
Двухсторонний шов: Ас= 2· 0,7Кb.
Пример 1. Дано: [σр] =160 МПа; [σсм] = 320 МПа; [τ] = 100 МПа;
в x δ =180 * 10мм
d = 20 мм
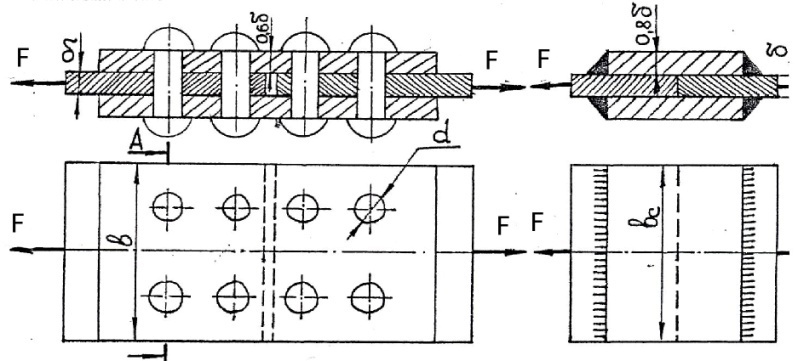
Рисунок
А
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ИМПЕРАТОРА АЛЕКСАНДРА I»
(ФГБОУ ВПО ПГУПС)
ПЕТРОЗАВОДСКИЙ ФИЛИАЛ
Практическое занятие 5
Практическое занятие 5
АЛГОРИТМ ВЫПОЛНЕНИЯ
1. Построить эпюру крутящих моментовпо длине вала для предложенной в задании схемы.
2. Выбрать рациональное расположение колес на валуи дальнейшие расчеты проводить для вала с рационально расположенными шкивами.
(Рациональное расположение колёс – расположение, при котором максимальное значение крутящего момента на валу – наименьшее из всех возможных.) Для экономии металла сечение бруса рекомендуется выполнить кольцевым
3. Определить потребные диаметры вала круглого и кольцевого сечения из расчета на прочность и жесткость и выбрать наибольшее из полученных значений, округлив величину диаметра.
4. Сравнить затраты металла для случая круглого и кольцевого сечений. Сравнение провести по площадям поперечных сечений валов.
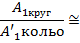
Площади валов рассчитать в наиболее нагруженном сечении (по максимальному крутящему моменту на эпюре моментов).
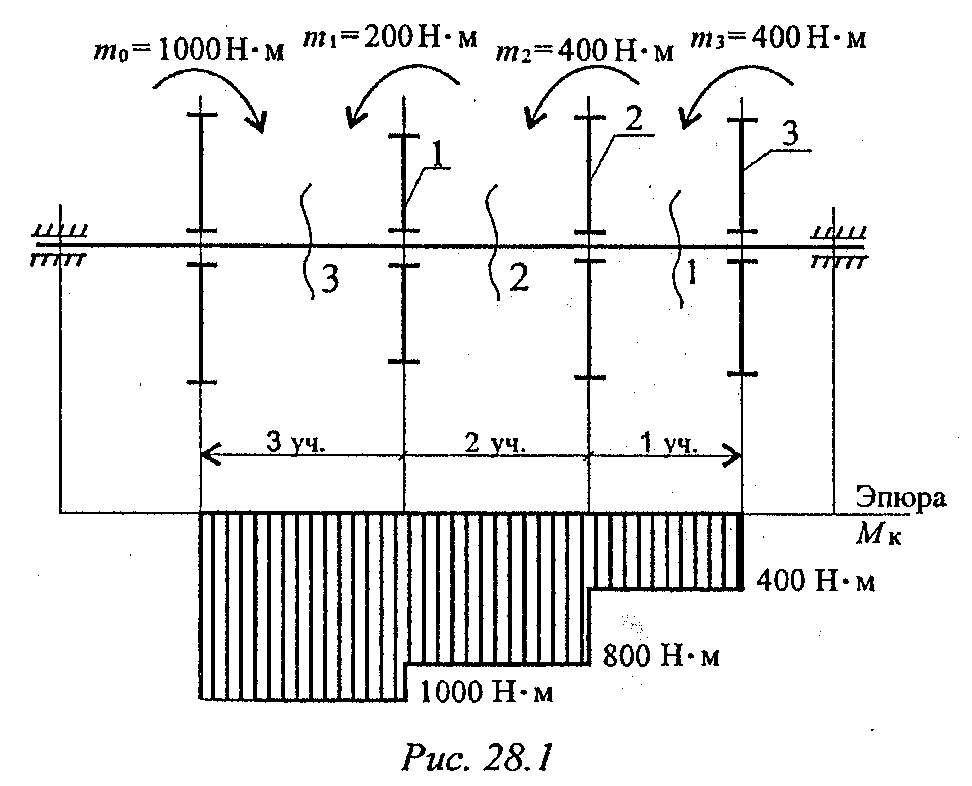 Пример. Для заданного бруса (рис. 28.1) построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном расположении шкивов.
Пример. Для заданного бруса (рис. 28.1) построить эпюры крутящих моментов, рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента. Построить эпюру крутящих моментов при рациональном расположении шкивов.
Из условия прочности определить диаметры вала для сплошного и кольцевого сечений, приняв 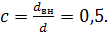 Сравнить полученные результаты по полученным площадям поперечных сечений. [τк] = 35 МПа.
Сравнить полученные результаты по полученным площадям поперечных сечений. [τк] = 35 МПа.
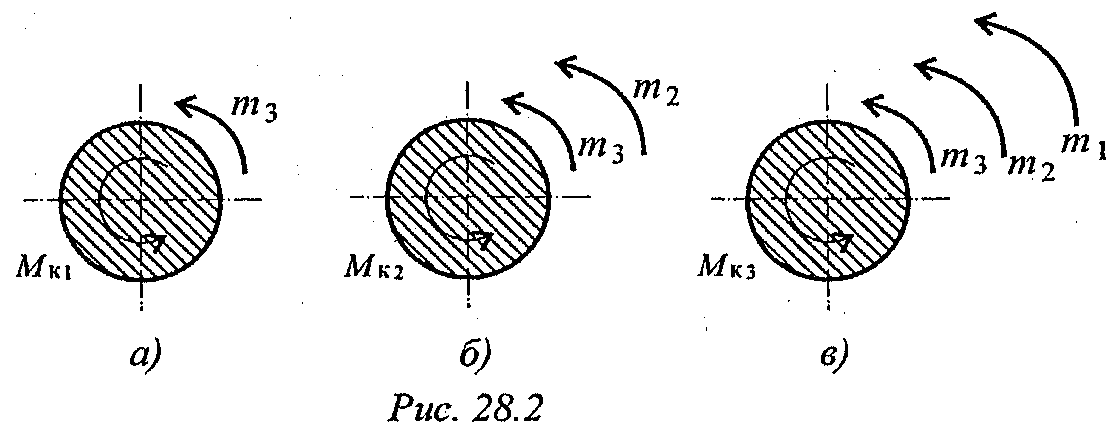 Решение
Решение
1. Пользуясь методом сечений, определяем крутящие моменты на участках вала (рис. 28.2).
Сечение 1 (рис. 28.2а):
Мк1 = m3 = 400 Н·м.
Сечение 2 (рис. 28.2б):
Мк2 = m3 + m2 = 800 Н·м.
Сечение 3 (рис. 28.2в):
Мк3 = mз + m2 + ml = 1000Н.м.
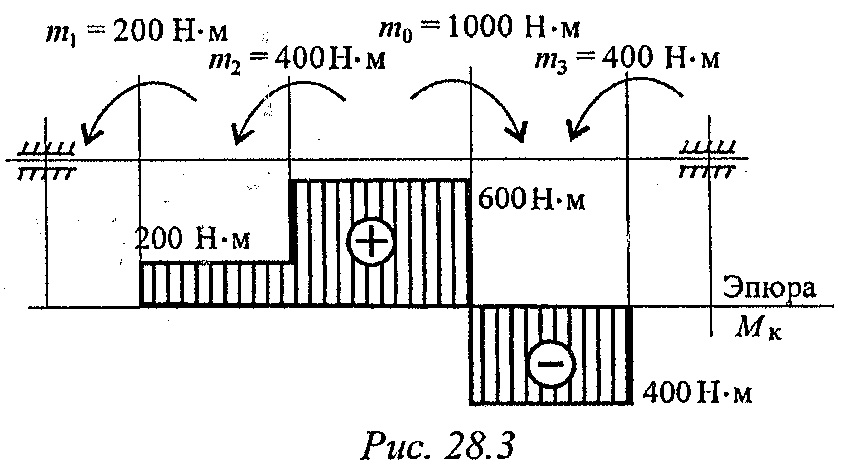 2. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т. к. моменты отрицательные.
2. Строим эпюру крутящих моментов. Значения крутящих моментов откладываем вниз от оси, т. к. моменты отрицательные.
Максимальное значение крутящего момента на валу в этом случае 1000Н.м (рис. 28.1).
3. Выберем рациональное расположение колес на валу. Наиболее целесообразно такое размещение колес, при котором наибольшие положительные и отрицательные значения крутящих моментов на участках будут по возможности одинаковыми. Из этих соображений ведущий шкив, передающий момент 1000Н.м, помещаем ближе к центру вала, ведомые шкивы 1 и 2 размещаем слева от ведущего с моментом 1000Н·м, шкив 3 остается на том же месте. Строим эпюру крутящих моментов при выбранном расположении шкива (рис. 28.3).
Максимальное значение крутящего момента на валу при выбранном расположении колес на валу 600 Н·м.
4. Определяем диаметры вала по сечениям при условии, что сечение - круг.
Условие прочности при кручении 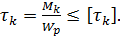
Момент сопротивления кручению
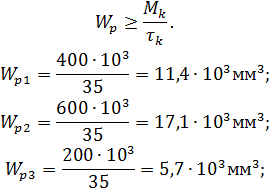
Определяем диаметры вала по сечениям:
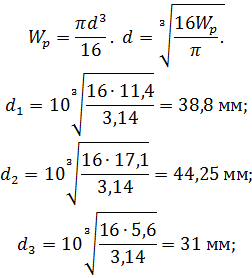
Округляем полученные значения: d1 = 40 мм; d2 = 45 мм; d3 = 35 мм.
5. Определяем диаметры вала по сечениям при условии, что сечение - кольцо.
Моменты сопротивления остаются теми же, По условию 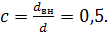
Полярный момент сопротивления кольца
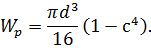
Формула для определения наружного диаметра вала кольцевого сечения будет следующей:
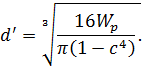
Расчет можно провести по формуле
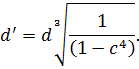
Диаметры вала по сечениям:
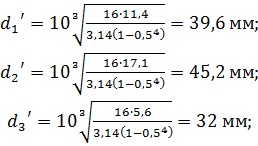
Наружные диаметры вала кольцевого сечения практически не изменились.
Для кольцевого сечения: d1’ = 40 мм; d2’ = 46 мм; d3’ = 35 мм.
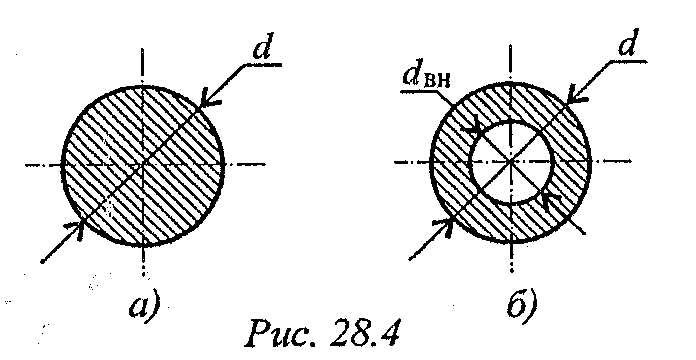
6. Для вывода об экономии металла при переходе на кольцевое сечение сравним площади сечений (рис. 28.4).
При условии, что сечение - круг (рис. 28.4а):
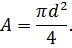
Сплошное круглое сечение:
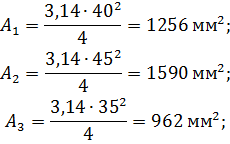
При условии, что сечение – кольцо, 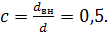 (рис. 28.46):
(рис. 28.46):
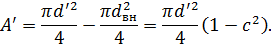
Кольцевое сечение:
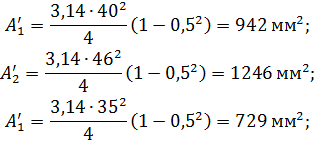
Сравнительная оценка результатов:
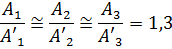
Следовательно, при переходе с кругового на кольцевое сечение экономия металла по весу составит 1,3 раза.
Задание:
1.Для стального вала круглого поперечного сечения определить значения внешних моментов, соответствующих передаваемым мощностям.
2.Построить эпюру крутящих моментов по длине вала.
3.Рациональным расположением шкивов на валу добиться уменьшения значения максимального крутящего момента на валу.
4.Построить эпюру крутящих моментов для этого случая.
5.Дальнейшие расчеты вести для вала с рациональным расположением шкивов.
6.Определить диаметры вала по сечениям из расчетов на прочность и жесткость. Полученный больший результат округлить до ближайшего четного или оканчивающегося на 5 числа.
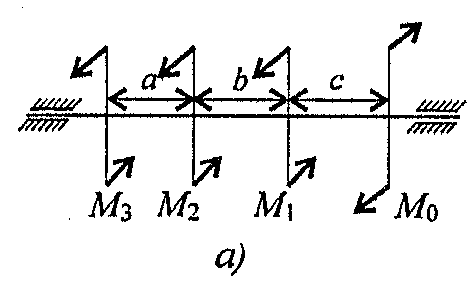
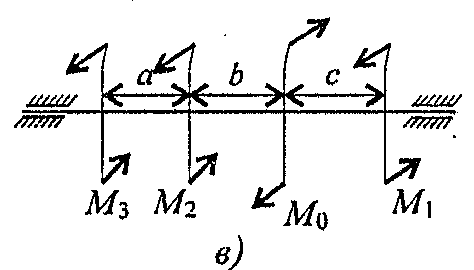
Данные взять из таблицы 7, схема 7.
Таблица 7
| Параметр | Вариант | |||||||||
| a = b = c, м | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 |
| P1, кВт | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 |
| P2, кВт | 2,6 | 2,7 | 2,8 | 2,9 | 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 |
| P3, кВт | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 |
Схема 7.
1.  | 2. 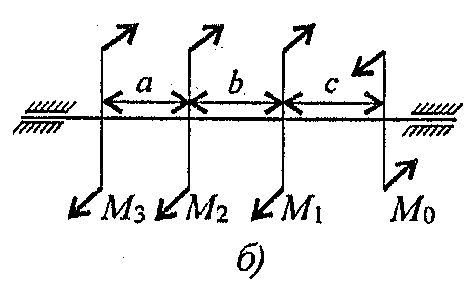 |
3.  | 4. 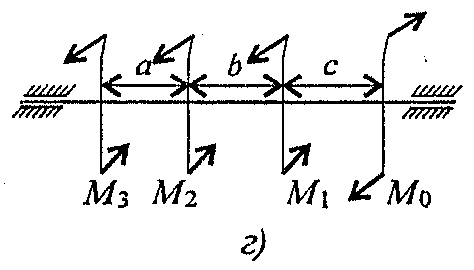 |
5. 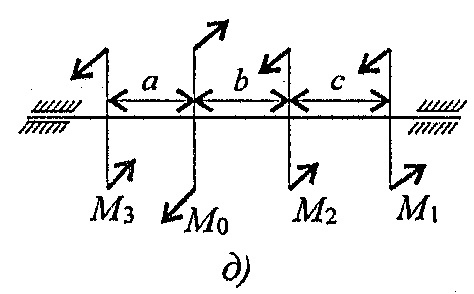 | 6. 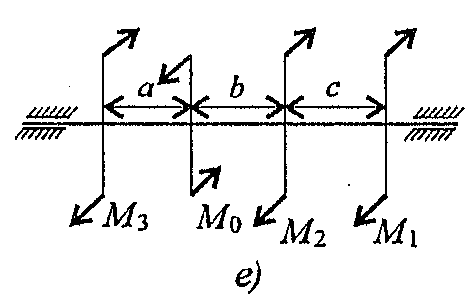 |
7.  | 8.  |
9.  | 10.  |
| Изм. |
| Лист |
