Оценка и определение ошибки при моделировании
При проведении экспериментов по моделированию какого-либо процесса важную роль играет изучение ошибок и неопределенностей. Результаты экспериментов содержат ошибки, которые могут быть как существенными, так и ничтожно малыми. Ни один эксперимент нельзя правильно спланировать без тщательного изучения этого фактора. Если неопределенности игнорируются или оцениваются небрежно, то это может приводить к убыткам, потере времени и труда.
Чтобы правильно поставить опыты по выбранной методике, необходимо заранее знать источники возможных ошибок. Кроме того, надо иметь в виду, что повышение точности иногда позволяет найти новые, неизвестные ранее закономерности. Поэтому для правильной постановки опыта производят предварительный анализ погрешности. К источникам возможных ошибок относятся: применение измерительных приборов невысокого класса точности и неправильная их настройка, неточная градуировка термопар, отклонение от расчетного теплового режима работы установки, недостаточно строгое выполнение граничных условий, с которыми связаны применяемые расчетные уравнения, неполный учет тепловых потерь, неспособность наблюдателя правильно регистрировать показания прибора и т.д.
Вышеназванные причины приводят к двум основным классам ошибок: систематические и случайные.
Систематические ошибки представляют собой фиксированные величины отклонения отсчета относительно известного или калиброванного значения независимо от того, сколько раз производится измерение, т.е. систематические ошибки имеют постоянные величины. Систематические ошибки могут быть легко устранены путем тщательной калибровки и проверки приборов и всей измерительной схемы или путем введения специальных поправок при обработке опытных данных.
Случайные ошибки имеют место, когда при последовательных измерениях постоянной величины получаются различные числовые значения. Величина ошибки зависит от того, насколько хорошо прибор может воспроизвести последовательные отсчеты при постоянном входном воздействии. Случайные ошибки являются принципиально неустранимыми. В некоторых случаях удается лишь уменьшить их численные значения.
Количественной оценкой точности результатов измерений является относительная ошибка. Относительная ошибка опыта представляет собой частное от деления абсолютной ошибки опыта 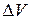 на абсолютное значение измеряемой величины
на абсолютное значение измеряемой величины 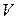 .
.
Если величина 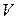 является заданной функцией нескольких независимых переменных, определяемых опытом,
является заданной функцией нескольких независимых переменных, определяемых опытом,
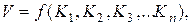
то 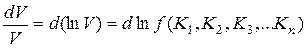
и относительная ошибка измерения 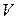 составит значение, равное сумме абсолютных значений всех слагаемых этих уравнений.
составит значение, равное сумме абсолютных значений всех слагаемых этих уравнений.
Это положение вытекает из того, что поскольку в первом приближении можно принять 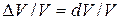 , а, как правило,
, а, как правило, 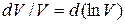 , то относительная ошибка одного опыта определяется полным дифференциалом от натурального логарифма измеряемой переменной величины
, то относительная ошибка одного опыта определяется полным дифференциалом от натурального логарифма измеряемой переменной величины 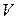 .
.
Рассмотрим определение коэффициента теплопроводности, который для плоской стенки неограниченных размеров выражается уравнением вида
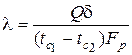 , (5.5)
, (5.5)
где 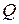 – тепловой поток;
– тепловой поток;
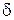 – толщина плоского слоя;
– толщина плоского слоя;
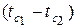 – перепад температур на изотермических поверхностях плоского слоя;
– перепад температур на изотермических поверхностях плоского слоя;
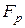 – расчетная поверхность, нормальная к направлению теплового потока.
– расчетная поверхность, нормальная к направлению теплового потока.
Логарифмируя уравнение (5.5), получим
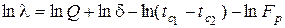 .
.
Полный дифференциал рассматриваемой функции будет иметь вид
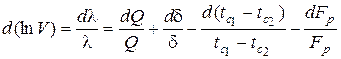 .
.
Следовательно, относительная ошибка измерений коэффициента теплопроводности составит величину
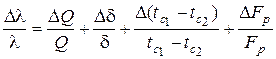 . (5.6)
. (5.6)
В выражении (5.6) 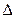 – абсолютные ошибки при измерении отдельных величин с помощью имеющихся приборов.
– абсолютные ошибки при измерении отдельных величин с помощью имеющихся приборов.
При умножении обеих частей уравнения (5.6) на 100 получим значение относительной ошибки по определению коэффициента теплопроводности в процентах. Аналогично относительная ошибка определяется и при измерении других величин, для этого необходимо знать расчетное уравнение, по которому определяется тот или иной параметр.
Пример. Определить максимальную относительную ошибку опыта по определению коэффициента теплоотдачи в трубе, если последний определяется
уравнением вида
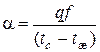 .
.
При этом удельный тепловой поток 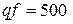 ккал/(м2·ч).
ккал/(м2·ч).
Температура поверхности трубы 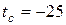 оС, жидкости – 35 оС.
оС, жидкости – 35 оС.
Измерение температуры производится с ошибкой 0,1 оС.
Максимальная относительная ошибка опыта в этом случае составит
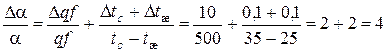 %.
%.
При проведении экспериментов оперируют средней арифметической и средней квадратичной ошибками. Для того, чтобы случайные ошибки результатов эксперимента были незначительными по сравнению с систематическими ошибками, каждый единичный опыт следует повторить достаточное количество раз.
При проведении п измерений единичного результата среднее арифметическое величин 
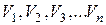 составит
составит
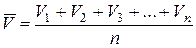
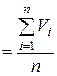 .
.
Средняя абсолютная арифметическая ошибка единичного результата при п измерениях выражается величиной
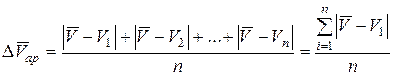 .
.
Средняя квадратичная ошибка единичного результата при п измерениях
представляется зависимостью
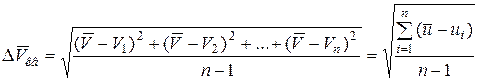 .
.
Относительные величины средних арифметической и квадратичной ошибок можно получить путем деления абсолютных их значений на величину 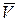 .
.
Чем больше проведено измерений, тем меньше влияние будут оказывать
случайные ошибки.
В отдельных случаях при определении полной ошибки к ошибкам измерения должна быть прибавлена ошибка отнесения.
Ошибка отнесения возникает тогда, когда какие-либо величины зависят от других величин. Например, коэффициент теплопроводности  , коэффициент температуропроводности
, коэффициент температуропроводности 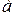 , теплоемкость
, теплоемкость 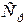 зависят от температуры. Поэтому измеренные их значения относят к какой-либо определенной температуре, например к средней.
зависят от температуры. Поэтому измеренные их значения относят к какой-либо определенной температуре, например к средней.
Однако эта средняя температура сама измеряется с некоторой абсолютной погрешностью 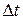 . В таком случае ошибка отнесения по температуре составит величину (если известна относительная скорость изменения изучаемой величины
. В таком случае ошибка отнесения по температуре составит величину (если известна относительная скорость изменения изучаемой величины  от температуры)
от температуры)
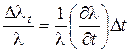 .
.
В случае зависимости измеряемой величины от нескольких параметров процесса ошибка отнесения будет иметь соответствующие слагаемые, учитывающие ошибки отнесения по всем этим параметрам.
