Моделирование конвективной теплопередачи

Конвективная теплопередача – это передача тепла с помощью конвекции от одной жидкости к другой через разделяющую их твердую стенку (рис.4.8). Ограничимся рассмотрением стационарного процесса вынужденного конвективного теплообмена.

Дифференциальные уравнения, характеризующие рассматриваемый процесс:

для жидкости 1:

уравнение движения

уравнение сплошности

уравнение переноса тепла

(4.134)

для разделяющей твердой стенки:

уравнение теплопроводности

(4.135)

для жидкости 2:

уравнение движения

уравнение сплошности

уравнение переноса тепла

(4.136)

Неуправляемые краевые условия могут быть получены исходя из следующих соображений. На поверхности твердых стенок, ограничивающих обе жидкости, скорости последних равны нулю, т.е.

. (4.137)

Автоматически также выполняется на поверхности раздела перегородки и жидкости 1 равенство температур и тепловых потоков, т.е.

(4.138)

Аналогичным образом для границы раздела стенки и жидкости 2 будем иметь:

(4.139)

Что касается теплообмена через наружные стенки теплообменного аппарата, то будем считать, что теплопотери отсутствуют, т.е.:

; . (4.140)

Управляемые краевые условия на границе входа жидкостей могут быть заданы уравнениями скорости и температуры потока:

(4.141)

(4.142)

Для уравнений (4.134)-(4.140) к безразмерному виду составим масштабные преобразования:

для жидкости 1:

для жидкости 2:

(4.143)

для стенки

4.144)

После введения преобразований (4.143) в уравнения (4.134)-(4.140) получим следующую систему уравнений связи:

(а') (а'')

(б') (б'')

(в') (в'')

(г') (г'') (4.145)

Выбрав произвольно масштабы для каждой системы и положив

получим следующие выражения для безразмерных величин:

(4.146)

Тогда дифференциальные уравнения и краевые условия в безразмерной форме будут следующими:

для жидкости 1:

; (4.147)

для твердой стенки

(4.148)

для жидкости 2:

. (4.149)

Неуправляемые краевые условия:

на поверхности твердых стен

на поверхности перегородки:

на наружных поверхностях стен

(4.150)

Управляемые краевые условия:

(4.151)

Решение системы дифференциальных уравнений (4.147)-(4.149), удовлетворяющее краевым условиям (4.150) и (4.151), может быть представлено в виде системы уравнений, каждое из которых представляет соответствующую безразмерную зависимую переменную как функцию безразмерных координат управляемых краевых условий и безразмерных физических параметров, входящих в систему дифференциальных уравнений и в краевых условиях. Так, например, температурные поля в обеих жидкостях и разделяющей их перегородке могут быть представлены уравнениями:

(4.152)

причем краевые условия задаются уравнениями (4.151).

Таким образом, для осуществления подобия температурных полей Т необходимо осуществить равенство критериев краевого подобия:

; ;

; , (4.153)

и равенство безразмерных параметров:

; ;

; . (4.154)

Выполнение условий (4.153) означает реализацию подобия на входных сечениях модели и образца или подобия управляемых краевых условий. Подобие неуправляемых краевых условий, выражаемых равенствами (4.150), осуществляется «автоматически», если выполнены условия (4.154). Осуществление этих условий существенно отличается, если жидкости 1 и 2, а также материалы стенок в модели и образца соответственно одинаковы, т.е. если:

.

В этом случае условия (4.154) осуществляются «автоматически». Однако экспериментальное исследование полей температур, скоростей и давлений во всем объеме модели является очень трудоемкой задачей. Поэтому при моделировании задач конвективного теплообмена обычно исследуют коэффициент теплопередачи k, определяемый из равенства:

(4.155)

где 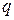– количество тепла, проходящего через единицу площади и в единицу времени, причем

где – температурный градиент на поверхности раздела жидкости;

– площадь перегородки, разделяющей обе жидкости;

и – средние температуры жидкости, причем способ усреднения произвольный.

Введя в уравнение (4.155) масштабные преобразования получим следующее уравнение связи:

(4.156)

где – критерий Кирпичева.

При выполнении условий (4.153) и (4.154) может иметь место равенство

или ,

откуда

. (4.157)

Таким образом, изменение коэффициента теплопередачи всего теплообменного аппарата в зависимости от различных факторов (скорости движения и температур жидкости, ее физических свойств, площади и формы перегородки и т.д.) может быть изучено на модели, а результаты исследований перенесены на образец.

4.10. Моделирование конвективного теплообмена при изменении
агрегатного состояния

Конвективный теплообмен с изменением агрегатного состояния имеет место при кипении жидкости, конденсации паров, кристаллизации и плавлении.

Вначале рассмотрим случай конвективного теплообмена при кипении жидкости или конденсации паров. Как показали экспериментальные исследования ряда ученых (С.С. Кутателадзе, С.И. Костерин и др.) можно считать, что жидкость, в которой происходит изменение агрегатного состояния, представляет собой двухфазную среду, состоящую из дискретных паровых и жидких областей. Для простоты изложения в дальнейшем будем считать обе фазы несжимаемыми, а физические параметры обеих фаз постоянными.

В этом случае процесс конвективной теплоотдачи через разделяющую стенку (рис.4.9) с изменением агрегатного состояния жидкости может быть описан следующей системой дифференциальных уравнений:

для первой фазы:

уравнение движения

;

уравнение неразрывности

;

уравнение переноса тепла

, (4.158)

для второй фазы:

уравнение движения

;

уравнение неразрывности

;

уравнение переноса тепла

, (4.159)

для твердой стенки:

уравнение теплопроводности

. (4.160)

Управляемые краевые условияопределяются заданием распределения скоростей и температур одной из фаз (например, первой фазы) во втором сечении теплообменного аппарата, а также заданием распределения коэффициента теплоотдачи на наружной поверхности твердой стенки, т.е.:

(4.161)

Неуправляемые краевые условияимеют место на границе соприкосновения каждой из фаз со стенкой, а также на границе раздела фаз.

На внутренней поверхности стенки должны иметь место равенства:

скоростей

тепловых потоков (4.162)
На поверхности раздела фаз должны иметь место равенства:

скоростей

сил трения

давлений

температур

;

тепловых потоков

* (4.163)

где – коэффициент поверхностного натяжения;

и – главные радиусы кривизны поверхности раздела фаз;

– температура кипения или конденсации;

– теплота фазового превращения;

– скорость перемещения границы раздела фаз;

* – выбор знака определяется тем, к какой из фаз обращена выпуклость поверхности раздела.

На наружной поверхности стенки должно быть обеспечено равенство количества подводимого тепла

(4.164)

После приведения с помощью масштабных преобразований уравнений (4.158)-(4.164) к безразмерному виду, получаем:

для первой фазы:

;

, (А)

для второй фазы

;

, (Б)

для стенки

(В)

Управляемые краевые условия:

(Г)

Неуправляемые краевые условия:

на внутренней поверхности стенки:

(Д)

на границе раздела фаз:

, (Е)

на наружной поверхности стенки:

При этом:

(Ж)

.

Решение безразмерных уравнений (А, Б, В), удовлетворяющее краевым условиям (Г, Д, Е, Ж), может быть представлено в виде системы равенств, каждое из которых выражает одну из безразмерных зависимых переменных как функцию безразмерных координат, времени, управляемых краевых условий и параметров, входящих в дифференциальные уравнения и граничные условия. Например, для решение может быть записано в виде

. (4.165)

Таким образом, для осуществления подобия, необходимо, чтобы при наличии геометрического подобия и в сходственные моменты времени должно быть обеспечено равенство соответствующих критериев модели и образца, т.е.:

или ; (4.166)

или ; (4.167)

или ; (4.168)

или (4.169)

или (4.170)

или (4.171)

или (4.172)

или (4.173)

или (4.174)

или (4.175)

или (4.176)

или (4.177)

или (4.178)

Моделирование конвективного теплообмена при кристаллизации или плавлении рассмотрим на примере образования ледопородного цилиндра в фильтрующих породах вокруг замораживающей колонки (рис.4.10).

Замораживание пород происходит благодаря постоянной циркуляции в колонке охлажденного до необходимой отрицательной температуры водного раствора хлористых солей натрия, магния или кальция.

Теплопередача в замороженных породах осуществляется путем теплопроводности и естественной конвекции, а в
фильтрующих породах еще и путем вынужденной конвекции. Известно, что замороженные породы представляют собой многофазную систему, состоящую из минеральных частиц, воды и льда. Необходимо отметить, что указанные фазы имеют различные термические сопротивления. В ряде исследований отмечается зависимость теплофизических свойств пород от температуры. Кроме того, установлено также, что в мелкозернистых породах на границе раздела мерзлых и талых пород не вся вода замерзает при 0 ^оС; в процессе замораживания наблюдается миграция влаги и, как следствие этого, имеют место процессы пучения и трещинообразования. Все эти обстоятельства затрудняют математическое выражение процесса теплопередачи в замороженных породах, и точных методов расчета процесса замораживания до настоящего времени не найдено.

Поэтому при исследовании подобных задач, учитывая их инженерный характер, прибегают к ряду упрощающих допущений. Принимают: замороженную и талую породы как изотропные; теплофизические свойства пород постоянными, но различными для талых и замороженных пород; замерзание среды происходит полностью при 0 ^оС; термическое сопротивление на границе промерзания отсутствует; замороженную породу как твердое тело, а фильтрующую среду как жидкость с усредненными теплофизическими свойствами; рассматриваемую задачу как плоскорадиальную; температуру теплоносителя в колонке по длине рассматриваемого участка постоянной.

Физическое моделирование процесса замораживания фильтрующих пород основывается на общей теории подобия тепловых и гидромеханических процессов, достаточно хорошо разработанной М.В. Кирпичевым, С.С. Кутателадзе, М.А. Михеевым и др. Согласно этой теории для реализации подобия температурных полей и тепловых потоков в натуре и на модели необходимо и достаточно соблюдения геометрического, гидромеханического, теплового и краевого подобия.

Из анализа дифференциальных уравнений, описывающих теплопередачу соответственно в замороженных и талых породах:

; (4.167)

, (4.168)

а также уравнений, описывающих краевые условия на границе раздела фаз и на границе хладоносителя со стенкой замораживающей колонки

; (4.169)

;

, (4.170)

где – теплота ледообразования, ккал/м³;

– размер замороженной зоны, м;

– пористость породы;

– линейный размер по направлению нормали к границе промерзания в рассматриваемой точке, м;

– коэффициент теплоотдачи теплоносителя, ккал/м²·ч· ^оС;

– температура хладоносителя, ^оС,

после приведения этих уравнений к безразмерному виду с помощью масштабных преобразований приходим к выводу о том, что для обеспечения подобия процесса замораживания фильтрующих пород необходимо выполнить равенство на модели и в натуре следующих критериев подобия:

(4.171)

где – коэффициент температуропроводности, м²/ч;

– время, ч;

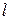– характерный линейный размер, м;

– критерий Фурье;

– скорость фильтрации и движения теплоносителя, м/ч;

– критерий Пекле;

– теплоемкость теплоносителя, ккал/(м³· ^оС);

– температура, ^оС;

– критерий Кутателадзе;

– коэффициент теплопроводности, ккал/(м·ч· ^оС);

– критерий инвариантности тепловых потоков;

– критерий Био.

Индекс «1» относится к области замороженных пород и температуре теплоносителя, индекс «2» – к области незамороженных пород и их начальной температуре, индекс – к замораживающей колонке, индекс – к теплоносителю.

Соблюдение условий подобия в общем случае (4.171) представляет значительные трудности, связанные в частности, с подбором исследуемой породы и рассола для модели по их физическим и теплофизическим характеристикам в соответствии с натурой и принятым геометрическим масштабом. В то же время нетрудно заметить, что условия моделирования упрощаются, если порода и теплоноситель на модели и в натуре одинаковы. В этом случае для обеспечения условий подобия необходимо выполнить равенство соотношений:

(4.172)

Выбрав линейный масштаб в качестве основного, из условий (4.172) получим, что определяющими являются следующие соотношения:

(4.173)

5. ИЗМЕРЕНИЕ ФИЗИЧЕСКИХ ПАРАМЕТРОВ
ПРИ МОДЕЛИРОВАНИИ. ОБОБЩЕНИЕ ДАННЫХ
И ОПРЕДЕЛЕНИЕ ОШИБКИ