Прямоугольные координаты на плоскости.

1. В треугольнике с вершинами , и проведена биссектриса . Тогда координаты точки равны … x= -7/3, y = 1.
2. Даны вершины треугольника , и . Тогда координаты точки пересечения медиан треугольника равны …(1;1) - точка пересечения, например, медиана АК и СМ, К(-3/2; 5/2), М(3;1).

3. Даны точки и . Тогда координаты точки , симметричной точке 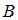относительно точки 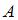, равны … (-7;4)(A – середина отрезка ВС ⟹ -3=(х_С+1)/2, 1=(у_С-2)/2)

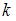4. Расстояние между точками и равно 2 при , равном …(1)

5. Точка симметрична точке относительно биссектрисы первого координатного угла. Тогда точка имеет координаты … (бисектриса 1-го координатного угла у=х).

6. Точки , и лежат на одной прямой. Тогда точка 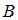делит отрезок в отношении … (λ=|AB|:|BC|)

7. В треугольнике с вершинами , и проведена медиана , длина которой равна …(4=|AM|, M(4; -1))

8. Даны три вершины параллелограмма: , , . Тогда четвертая вершина , противолежащая вершине 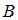, имеет координаты …(-3;-1)

Прямая на плоскости.

1. Уравнение геометрического места точек, равноудаленных от двух данных точек и , имеет вид … (проходит через средину ВС и перепендикулярна вектору ВС=(4;2)).

2. Прямая линия проходит через точки и . Тогда она пересекает ось 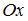в точке … (уравнение прямой через 2 точки)

3. Площадь треугольника, образованного пересечением прямой с осями координат, равна …(54) (уравнение прямой в отрезках: х/9+у/12=1, отрезки, отсекаемые на осях: 9 и 12).

4. Прямые и …перпендикулярны (их нормальные векторы (4; -5) ⊥(5;4)).

5. Прямая отсекает на оси отрезок и имеет угловой коэффициент 2/3. Тогда ее уравнение имеет вид … (у=кх+b, k=2/3).

6. Прямые и пересекаются в точке, лежащей на оси абсцисс. Тогда эта точка имеет координаты …(2;0)

7. Прямая задана в параметрическом виде . Тогда ее общее уравнение имеет вид …

Кривые 2-го порядка.

1. Фокусы эллипса имеют координаты и , а его эксцентриситет равен 0,6. Тогда каноническое уравнение эллипса имеет вид …

2. Вершина параболы имеет координаты … (выделение полного квадрата по x: (x-1)²=2(y-7))

3. Радиус окружности равен … (2) (выделение полного квадрата по х и по у)

4. Уравнение директрисы параболы, проходящей через точки , и симметричной относительно оси 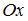, имеет вид …

Решение:
Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси 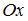имеет вид: , а уравнение директрисы: . Параметр находится из условия, что точка принадлежит параболе, то есть , . Тогда уравнение директрисы параболы примет вид: .

5. Соотношение в прямоугольной декартовой системе координат задает …(параболу)

6. Центр окружности имеет координаты …

7. Расстояние между фокусами гиперболы равно …(10)

8. Асимптоты гиперболы задаются уравнениями …y=3x/2 и y= - 3x/2.

Плоскость в пространстве.

1. Плоскость проходит через точку и отсекает на осях абсцисс и ординат в положительных направлениях отрезки длины 3 и 5 соответственно. Тогда общее уравнение плоскости имеет вид … (можно просто подставить координаты точки в данные уравнения).

2. Общее уравнение плоскости, проходящей через точку перпендикулярно прямой , имеет вид … (из уравнения прямой нормальный вектор плоскости (2,3,-1)).

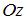3. Плоскость, проходящая через точки и параллельно оси , задается уравнением … (z –в уравнении отсутствует, координаты точек удовлетворяют уравнению)

3.Геометрическое место точек, удаленных от плоскости на 2 единицы, может иметь вид …

4. Уравнение плоскости, проходящей через точку параллельно векторам и , имеет вид … (нормальный вектор плоскости – векторное произведение векторов а и b,а координаты точки удовлетворяют уравнению)

5. Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид … (можно подставить координаты точки в данные уравнения)

6. Уравнение плоскости, проходящей через точки , и , имеет вид …

7. Плоскости и перпендикулярны при значении , равном …m=4.