Линейная зависимость векторов. Базис
Рассмотрим n векторов и  1,
1,  2, …,
2, …,  n и n чисел
n и n чисел  .
.
def. Выражение вида l1 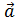 1 + l2
1 + l2  2 + … + ln
2 + … + ln  n называется линейной комбинацией
n называется линейной комбинацией
векторов  1,
1,  2, …,
2, …,  n.
n.
def. Векторы  1,
1,  2, …,
2, …,  n называются линейно зависимыми, если существуют такие числа
n называются линейно зависимыми, если существуют такие числа  , не все равные нулю одновременно, что
, не все равные нулю одновременно, что
l1 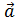 1 + l2
1 + l2  2 + … + ln
2 + … + ln  n =
n = 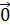 .
.
Например,  , тогда l1
, тогда l1 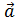 1 = - l2
1 = - l2  2 - … - ln
2 - … - ln  n,
n,
 1 = -
1 = - 
 2 - … -
2 - … - 
 n Þ
n Þ  1 есть линейная комбинация
1 есть линейная комбинация  1,
1,  2, …,
2, …,  n.
n.
Итак, если векторы линейно зависимы, то хотя бы один из них можно представить в виде линейной комбинации остальных векторов.
Справедливо и обратное утверждение.
def. Векторы  1,
1,  2, …,
2, …,  n называются линейно независимыми, если равенство
n называются линейно независимыми, если равенство
l1 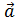 1 + l2
1 + l2  2 + … + ln
2 + … + ln  n =
n = 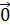 возможно тогда и только тогда, когда
возможно тогда и только тогда, когда

Замечания.
1) Любые два коллинеарных вектора на плоскости линейно зависимы.
2) Любые два неколлинеарных вектора на плоскости линейно независимы.
Таким образом, для того, чтобы два вектора на плоскости были линейно независимы, необходимо и достаточно, чтобы они были неколлинеарные.
Теорема. Если на плоскости заданы два неколлинеарных вектора  и
и  , то любой третий вектор
, то любой третий вектор  плоскости может быть представлен в виде линейной комбинации векторов
плоскости может быть представлен в виде линейной комбинации векторов  и
и  , т.е.
, т.е.
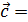 l1
l1 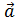 + l2
+ l2  . (1)
. (1)
Доказательство.
По условию векторы  и
и  – неколлинеарные.
– неколлинеарные.
1) Предположим, что 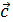 неколлинеарен векторам
неколлинеарен векторам  и
и  . Построим параллелограмм, где
. Построим параллелограмм, где  является диагональю, а стороны лежат на векторах
является диагональю, а стороны лежат на векторах  и
и  .
.
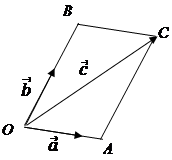
2) Пусть 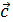 коллинеарен
коллинеарен  или
или  , например,
, например, 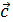 коллинеарен
коллинеарен  Þ
Þ
Теорема доказана.
Следствие 1. Всякие три вектора на плоскости линейно зависимы.
Следствие 2. Если число данных векторов на плоскости больше трех, то они линейно зависимы.
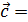 l1
l1 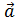 + l2
+ l2  Þ
Þ 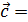 l1
l1 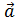 + l2
+ l2  + 0 ×
+ 0 × 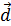 + … + 0 ×
+ … + 0 × 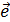 Þ линейно зависимые.
Þ линейно зависимые.
Вывод. Максимальное число линейно независимых векторов на плоскости равно двум.
Аналогично доказывается:
1. Для того чтобы три вектора в пространстве были линейно независимы, необходимо и достаточно, чтобы они были некомпланарные.
2. Если  ,
,  ,
,  - три некомпланарных вектора пространства, то любой четвертый вектор
- три некомпланарных вектора пространства, то любой четвертый вектор 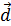 пространства может быть представлен в виде линейно комбинации векторов
пространства может быть представлен в виде линейно комбинации векторов  ,
,  ,
,  .
.
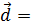 l1
l1 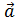 + l2
+ l2  + l3
+ l3  . (2)
. (2)
3. Всякие четыре и более векторов пространства линейно зависимы.
Вывод. Максимальное число линейно независимых векторов в пространстве равно трем.
def. Базисом на плоскости называется два любых линейно независимых вектора
плоскости, т.е. пара неколлинеарных векторов.
Базисом в пространстве называется три любых линейно независимых вектора пространства, т.е. тройка некомпланарных векторов.
Рассмотрим разложение (1) на плоскости 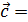 l1
l1 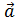 + l2
+ l2  , где
, где  и
и  - неколлинеарные.
- неколлинеарные.
Коэффициенты 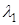 и
и 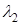 называются координатами вектора
называются координатами вектора  в базисе
в базисе  ,
,  .
.
Аналогично для разложения (2): 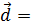 l1
l1 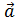 + l2
+ l2  + l3
+ l3  , где
, где  ,
,  ,
, 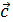 - некомпланарные векторы пространства.
- некомпланарные векторы пространства.
Коэффициенты 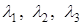 называются координатами вектора
называются координатами вектора 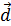 в базисе
в базисе  ,
,  ,
, 
Замечания.
1.Если определитель, составленный из координат двух векторов плоскости, отличен от нуля, то эти векторы линейно независимы на плоскости, т.е. образуют базис на плоскости.
2.Если определитель, составленный из координат трех векторов пространства R3, отличен от нуля, то эти векторы линейно независимы в пространстве, т.е. образуют базис в R3.
Пример 4.1. Доказать, что векторы  1 = (2; 0; 0),
1 = (2; 0; 0),  2 = (0; 1; 0),
2 = (0; 1; 0), 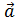 3 = (0; 0; 0,5) образуют базис в R3. Найти координаты
3 = (0; 0; 0,5) образуют базис в R3. Найти координаты 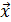 = (2; - 4; 15) в этом базисе, т.е. разложить вектор
= (2; - 4; 15) в этом базисе, т.е. разложить вектор 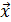 по базису
по базису  1,
1,  2,
2,  3. Ответ:
3. Ответ: 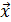 =
=  1 - 4
1 - 4  2 + 3
2 + 3  3.
3.
