Метод наложения (суперпозиции)

Предполагается, что если в электрической цепи действует несколько источников энергии (ЭДС и тока), то ток в каждой ветви данной цепи (цепь линейная) может быть найден как алгебраическая сумма токов, рассчитанных отдельно от каждого источника. Так, для схемы на рис. 3.2 следует рассмотреть две схемы: с источником ЭДС (рис. 3.5) и с источником тока J (рис. 3.6). Тогда токи в ветвях схемы рис. 3.2 получаются как результат алгебраического суммирования частных токов и .

Метод суперпозиции позволяет, рассматривая упрощенные схемы, имеющие по одному источнику энергии, определить все требуемые токи и напряжения.

Рис. 3.5	Рис. 3.6

При использовании метода суперпозиции необходимо выполнять следующие правила:

1. Исходная схема разбивается на более простые схемы с одним источником энергии (сколько источников энергии, столько и схем).

2. Источники тока при исключении их из схемы размыкаются, а источники ЭДС при их исключении из схемы закорачиваются. Внутренние сопротивления источников ЭДС и тока во всех схемах учитываются.

3. Частные токи имеют свои направления, определяемые источниками энергии в данной частной схеме.

Недостаток метода суперпозиции – большое количество схем для рассмотрения.

Метод контурных токов (МКТ)

Контурный ток – ток, имеющий в рассматриваемом контуре во всех его ветвях одно и то же значение, как по величине, так и по направлению. В общем случае контурный ток не равен току в ветви. Совпадает контурный ток только в ветви с источником тока, а также в любой внешней ветви. Ток в смежной ветви определяется алгебраическим суммированием контурных токов. Сопротивления смежных ветвей называются взаимными сопротивлениями.

Матричное уравнение для метода контурных токов

, (3.1)

где – квадратная матрица сопротивлений; – матрица контурных токов; – матрица задающих источников ЭДС, в которой со знаком «+» записывают те источники ЭДС, которые по направлению совпадают с контурными токами.

В матрице сопротивлений символами обозначены собственные сопротивления контуров, равные сумме сопротивлений ветвей, входящих в данный контур, а символами – взаимные сопротивления между контурами, определяемые сопротивлениями ветвей между контурами (смежных ветвей).

По методу контурных токов количество 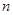уравнений определяется количеством независимых контуров и равно . Поскольку контурный ток, проходящий через источник тока, равен величине тока источника тока, то такой контур не рассматривается.

Поскольку в форме записи (3.1) присутствуют только задающие источники ЭДС, то независимые источники тока должны быть эквивалентно преобразованы в источники ЭДС.

Проведя для рассмотренной ранее схемы (рис. 3.2) указанное эквивалентное преобразование (рис. 3.3) и выбрав направления контурных токов и , получим схему, приведенную на рис. 3.7.
Рис. 3.7

Матрица сопротивлений для данной схемы имеет вид , где – контурные сопротивления, которые всегда положительны, а знак любого взаимного сопротивления определяется направлениями контурных токов: если в ветви с этим сопротивлением контурные токи совпадают по направлению, то перед соответствующим взаимным сопротивлением ставится знак «+», если противоположны – то знак «–». Для схемы на рис. 3.7 собственное сопротивление первого контура равно ; собственное сопротивление второго контура равно ; взаимное сопротивление равно ; задающая ЭДС в контуре с током равна ; задающая ЭДС в контуре с током равна .

Система уравнений, описывающая схему (рис. 3.7) и соответствующая матричному уравнению (3.1) имеет вид:

. (3.2)

Главный определитель системы уравнений (3.2)

.

В результате решения уравнений системы (3.2) находят контурные токи.

Ток в первом контуре , где – получено заменой первого столбца главного определителя системы (3.2) элементами столбцовой матрицы задающих источников ЭДС. Тогда контурный ток .

Ток во втором контуре , где получено заменой второго столбца главного определителя системы (3.2) элементами столбцовой матрицы задающих источников ЭДС. Тогда контурный ток .

Токи в ветвях определяются через контурные токи:

.

Использование метода контурных токов позволяет:

1. Уменьшить количество уравнений по сравнению с количеством уравнений, составляемых по законам Кирхгофа. Для рассматриваемой схемы (рис. 3.2) число уравнений, составленных по законам Кирхгофа, равно , а по методу контурных токов число уравнений равно .

2. Уменьшить количество рассматриваемых схем по сравнению с методом наложения.

3. Применять вычислительную технику для реализации матричных методов расчета.

Метод узловых потенциалов

Метод узловых потенциалов (МУП) также основан на использовании законов Кирхгофа. Количество уравнений по МУП , где – количество узлов. Таким образом .

Матричное уравнение для МУП

, (3.3)

где

– квадратная матрица проводимостей;

– матрица узловых потенциалов;

– матрица задающих источников тока.

При использовании МУП потенциал одного из узлов полагается равным нулю, а источники ЭДС эквивалентно преобразуются в источники тока.

Рассмотрим применение МУП на примере схемы, приведенной на рис. 3.2. Для этой схемы количество уравнений . Положив потенциал узла 3 равным нулю ( ) и осуществив эквивалентное преобразование источника ЭДС в источник тока , получим схему, изображенную на рис. 3.8.

Рис. 3.8

Для этой схемы матрица проводимостей , где – узловые проводимости (суммы проводимостей всех ветвей, входящих в узел), определяемые в соответствии с выражениями: – взаимные проводимости – проводимости ветвей между узлами, определяемые в соответствии с выражением – матрица узловых потенциалов; – матрица задающих источников тока, в которой , .

Таким образом, система уравнений имеет вид:

(3.4)

Решение системы уравнений (3.4), состоящее в определении потенциалов и , такое же, как и в методе контурных токов: , где – главный определитель системы уравнений (3.4); – получено заменой первого столбца в главном определителе элементами матрицы задающих токов; – получено заменой второго столбца в главном определителе элементами матрицы задающих токов.

Тогда решение системы (3.4):

и .

Правила при решении методом узловых потенциалов:

1. Один узел выбирается базисным, с .

2. Все источники ЭДС эквивалентно преобразуются в источники тока.

3. Знаки в матрице проводимостей строго соответствуют приведенному примеру, узловые проводимости положительны, а взаимные – отрицательны.

4. В задающих источниках тока со знаком «+» записываются втекающие токи, со знаком «–» – вытекающие.

5. Токи в ветвях определяются путем применения закона Ома для участка цепи ( ). Для определения токов в ветвях необходимо вернуться к исходной схеме (рис. 3.2) и определить значения токов в ветвях: .