Практическое занятие 7. Расчеты динамики падения среднего давления и объемов вторжения воды по заданной динамике отборов нефти
Теоретическая часть
Основные параметры теории упругого режима. Коэффициент объемной упругости жидкости и пласта.
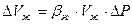 (3.1)
(3.1)
Коэффициент объемной упругости воды 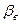 изменяется в зависимости от давления, температуры, количества растворенного газа. В некоторых диапазонах
изменяется в зависимости от давления, температуры, количества растворенного газа. В некоторых диапазонах 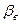 можно считать постоянным.
можно считать постоянным.
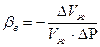
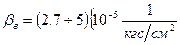 ,
, 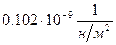
Пласт считается однородной упругой средой, подчиняющейся закону Гука. Относительное изменение порового объема пласта пропорционально изменению давления. Скелет породы испытывает давление
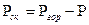
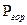 - горное давление,
- горное давление, 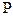 - давление флюида, считая горное давление постоянным
- давление флюида, считая горное давление постоянным 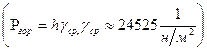
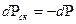
Сжимаемость скелета 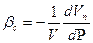 , здесь V- выделенный объем пласта, Vп - поровый объем.
, здесь V- выделенный объем пласта, Vп - поровый объем.
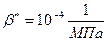 ,
, 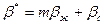
Если пласт замкнутый, эксплуатируется при упругом режиме, то добыча нефти за период падения, средневзвешенного давления Р0 - 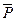 составит упругий запас
составит упругий запас
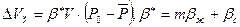
C другой стороны, отобрано жидкости за время t:
q·t
Уравнение баланса:
q·t = 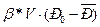 .
.
Если рассматривать малый период "dt", взять дифференциал баланса:
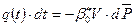 ,
,
получим дифференциальное уравнение:
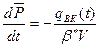
Рассмотрим нефтяную залежь, окруженную водным бассейном. Законтурную область плоскорадиальной фильтрации воды от удаленного контура R∞ до контура нефтеносности залежи Rк представим как замкнутую. Тогда для неё аналогичное уравнение материального баланса, как для замкнутого контура нефтяной залежи:
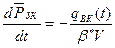 (3.2)
(3.2)
здесь 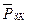 - средневзвешенное давление законтурной области;
- средневзвешенное давление законтурной области;
qВК (t) – расход воды в нефтяную залежь.
Приняв приближенно фильтрацию воды в водном бассейне стационарной по Дюпюи:
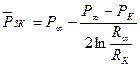 , (3.3)
, (3.3)
получим:
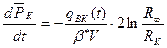 ,
, 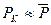 (3.4)
(3.4)
Пусть нефтяная залежь эксплуатируется при водонапорном режиме с притоком воды через контур нефтеносности. Тогда исходный баланс:
q·t = 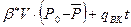 .
.
Так, упругий баланс составит:
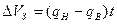 . (3.5)
. (3.5)
Дифференциальное уравнение материального баланса:
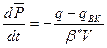 (3.6)
(3.6)
В этом случае падение давления меньше, чем для замкнутого пласта.
Задача 1.Определить динамику падения среднего давления и объемов вторжения воды по заданной динамике отборов нефти.
Система интегральных уравнений залежи нефти (как укрупненной скважины в водоносном пласте) имеет вид:
P(t) – Pнач. = – (Qдоб.н – Qв.)/βнVн (3.7)
P(t) – Pнач. = – (Qв. 2 ln(Rk/Rус))/ βвVв (3.8)
Qзап.н= Рнач. βн Vн – добываемые запасы нефти.
Заданно количество добытой нефти Qдоб.н по вариантам:
Qдоб.н = 0.05 Qзап.н, 0.1 Qзап.н, …….0.8 Qзап.н.
В уравнение подставляется Qдоб.н, уравниваются правые части уравнений и из полученного равенства находят Qв. Далее из уравнения 2 находят P(t).
Исходные данные: Vн= 108 м3, Vв= 109 м3, βн=10-41/атм, βв=10-51/атм, Pнач.=100 атм, Rk/Rус=10, ln(Rk/Rус)= 2,3;
Практическое занятие 8. Идентификация нефтяной залежи, эксплуатируемой в замкнутом упругом режиме
Постановка задачи.
Если замкнутый контур эксплуатируется при упругом режиме, уравнение истощения:
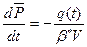 ,
,
где V - объём пласта,
β* - упругоемкость,
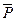 - средневзвешенное давление.
- средневзвешенное давление.
Падение давления за время t = 0 до момента t:
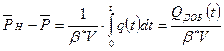 (1)
(1)
или 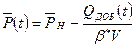 ,
,
т.е. прямая линия при 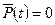 ,
, 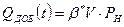
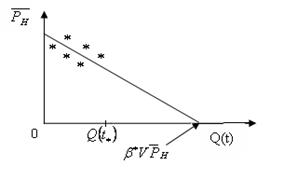
Коэффициент "β*V" в уравнении истощения нельзя определить точно по данным геолого-физических исследований. Если имеются данные истории эксплуатации месторождения от t = 0 до t = t* замеров:
 t1 {
t1 {  ~
~ 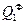 }
}
t2 { 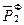 ~
~ 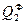 } (2)
} (2)
- - - - - - - - -
t* { 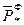 ~
~ 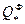 }
}
то методом наименьших квадратов находят коэффициент 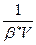 в уравнении, а следовательно, полный упругий запас нефти
в уравнении, а следовательно, полный упругий запас нефти 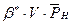 .
.
Пример решения поставленной задачи.
Обозначим 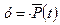 ,
, 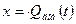 ,
, 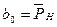 ,
, 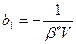 .
.
Уравнение (1) перепишем в следующих обозначениях:
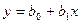 (3)
(3)
Данные замеров (2) представляют набор экспериментальных данных 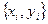 , i = 1,2,3, …..n
, i = 1,2,3, …..n
Уравнение 3 представляет уравнение линейной регрессии и описывает зависимость между величинами 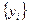 и
и 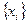 .
.
Требуется определить коэффициент b1 в соответствии с методом обработки наблюдений случайных величин – методом наименьших квадратов.
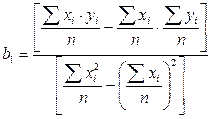 (4)
(4)
Далее определяем полный упругий запас нефти по формуле:

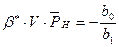
Исходные данные замеров давлений (атм):
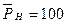 ,
, 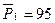 ,
, 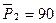 ,
, 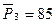 ,
, 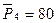 ,
, 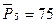 ,
, 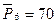 ,
, 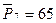
Варианты работ
Таблица 1 – Числовые значения Qдоб (t) [млн. м3]
| № варианта | |||||||
