Практическое занятие 2. Приближенное решение уравнения пьезопроводности при условии постоянного дебита скважины. Расчеты P(r,t)
МИНИCTEPCTBO ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению практических занятий по дисциплине
«Математическое моделирование в задачах нефтегазовой отрасли.
Методы математической физики»
для магистров направления
130500.68 «Нефтегазовое дело»
Ставрополь, 2013
Методические указания по выполнению практических занятий по дисциплине «Математическое моделирование в задачах нефтегазовой отрасли. Методы математической физики», составлены на основании рабочего учебного плана и программы для магистров направления 130500.68 «Нефтегазовое дело».
Составитель: Коршунова Л. Г., Якушев А.В.
Содержание
Практическая занятие 1. Вывод уравнения пьезопроводности. 4
Практическое занятие 2. Приближенное решение уравнения пьезопроводности при условии постоянного дебита скважины. Расчеты P(r,t) 6
Практическое занятие 3. Параметры укрупненной модели нефтяного пласта. Определение упругого запаса. Расчеты добычи нефти и объемов внедрения воды по заданной динамике падения среднего давления. 9
Практическое занятие 4. Расчёт показателей разработки
газового месторождения. 13
Практическое занятие 5. Определение скорости потока промывочной жидкости, необходимой для очистки забоя скважины.. 17
Практическое занятие 6. Расчёт коэффициента корреляции. Определение уравнения регрессии. 18
Практическое занятие 7. Расчеты динамики падения среднего давления и объемов вторжения воды по заданной динамике отборов нефти. 21
Практическое занятие 8. Идентификация нефтяной залежи, эксплуатируемой в замкнутом упругом режиме. 24
Практическое занятие 9. Метод суперпозиций. Решение уравнения пьезопроводности по заданной динамике притока вод. 27
Практическое занятие 10. Метод суперпозиций. Решение уравнения пьезопроводности по заданной динамике падения давления на контуре укрупненой скважины.. 30
Практическое занятие 11. Сеточная модель. Элементы структуры. Вывод уравнения фильтрации однофазного флюида. 33
Практическое занятие 12. Фазовые состояния. 37
Практическое занятие 13. Математическая модель фазовых проницаемостей. 39
Практическое занятие 14. Уравнение фильтрации двух-трех фаз. 40
Практическое занятие 15. Определение основных параметров трёхфазной модели нелетучей нефти Маскета-Мереса. 43
Практическое занятие 16. Вывод уравнений неразрывности течения для трёхфазной модели нелетучей нефти Маскета-Мереса. 45
Практическое занятие 17. Многофазная многокомпонентная фильтрация. Трехфазная – двух-трехмерная фильтрация. 48
Практическая занятие 1. Вывод уравнения пьезопроводности
Пласт одноразовый, скважина в центре, поток радиально-симметричный. Жидкость слабосжимаема.
 Выделим кольцевой элемент
Выделим кольцевой элемент 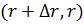 .
.
Составим расход массы жидкости через грани элемента за время 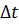 .
.
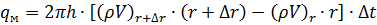
Составим изменение запаса жидкости за время 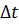 , полагая что за этот промежуток давление изменилось на
, полагая что за этот промежуток давление изменилось на 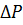 .
.
Объём элемента 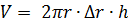 . Объём жидкости в элементе
. Объём жидкости в элементе 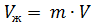 .
.
По определению коэффициента сжимаемости жидкости:
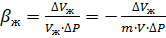 à
à 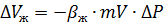
Изменение запаса жидкости в элементе 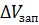 происходит за счёт изменения объёма
происходит за счёт изменения объёма 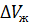 и изменения объёма скелета
и изменения объёма скелета 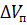 :
:
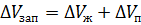
По определению, сжимаемость скелета породы:
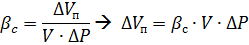
Тогда изменение запаса:
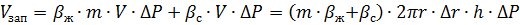 ;
; 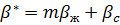
Записываем равенство 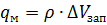 и разделим на
и разделим на  сократив множитель
сократив множитель 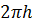
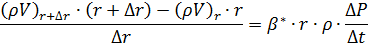
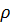 - плотность жидкости.
- плотность жидкости.
Ввиду малой сжимаемости изменениям плотности в пределах кольцевого элемента можно пренебречь и сократить в уравнении величину « 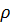 ». Переходя к пределу при
». Переходя к пределу при 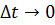 ,
, 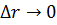 , получим уравнения неразрывности в виде:
, получим уравнения неразрывности в виде:
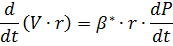
По закону Дарси 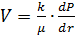 , коэффициент пьезопроводности ᴂ
, коэффициент пьезопроводности ᴂ 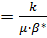 После подстановок уравнение неразрывности принимает вид:
После подстановок уравнение неразрывности принимает вид:
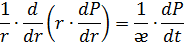
После дифференцирования в правой части уравнения неразрывности оно принимает вид, принятый под названием уравнения пьезопроводности:
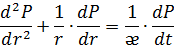
Постановка задачи.
Если замкнутый контур эксплуатируется при упругом режиме, уравнение истощения:
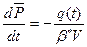 ,
,
где V - объём пласта,
β* - упругоемкость,
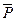 - средневзвешенное давление.
- средневзвешенное давление.
Падение давления за время t = 0 до момента t:
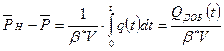 (1)
(1)
или 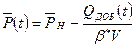 ,
,
т.е. прямая линия при 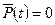 ,
, 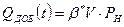
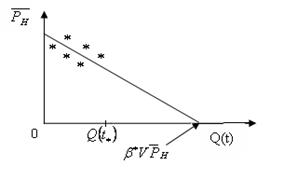
Коэффициент "β*V" в уравнении истощения нельзя определить точно по данным геолого-физических исследований. Если имеются данные истории эксплуатации месторождения от t = 0 до t = t* замеров:
 t1 {
t1 { 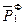 ~
~ 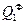 }
}
t2 { 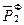 ~
~ 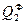 } (2)
} (2)
- - - - - - - - -
t* { 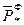 ~
~ 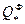 }
}
то методом наименьших квадратов находят коэффициент 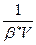 в уравнении, а следовательно, полный упругий запас нефти
в уравнении, а следовательно, полный упругий запас нефти 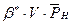 .
.
Пример решения поставленной задачи.
Обозначим 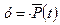 ,
, 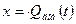 ,
, 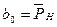 ,
, 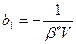 .
.
Уравнение (1) перепишем в следующих обозначениях:
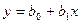 (3)
(3)
Данные замеров (2) представляют набор экспериментальных данных 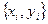 , i = 1,2,3, …..n
, i = 1,2,3, …..n
Уравнение 3 представляет уравнение линейной регрессии и описывает зависимость между величинами 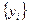 и
и 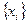 .
.
Требуется определить коэффициент b1 в соответствии с методом обработки наблюдений случайных величин – методом наименьших квадратов.
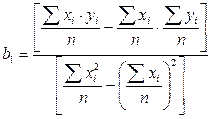 (4)
(4)
Далее определяем полный упругий запас нефти по формуле:

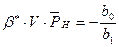
Исходные данные замеров давлений (атм):
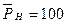 ,
, 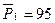 ,
, 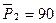 ,
, 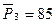 ,
, 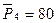 ,
, 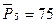 ,
, 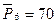 ,
, 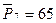
Варианты работ
Таблица 1 – Числовые значения Qдоб (t) [млн. м3]
| № варианта | |||||||
Список литературы
1. Кудинов, В. И. Основы нефтегазопромыслового дела [Текст] / В. И. Кудинов. − Москва-Ижевск: Институт компьютерных исследований; Удмуртский госуниверситет. 2004. − 720 с.
2. Совершенствование разработки нефтяных месторождений на завершающей стадии/Н.Н. Лисовский, М.М. Иванова, В.Ф. Базив, В.М. Малюгин//Нефтяное хозяйство. – 2008. - № 3. – С. 22-24.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению контрольной работы по дисциплине
«Математическое моделирование процессов нефтеизвлечения»
для магистров направления
130500.68 «Нефтегазовое дело»
МИНИCTEPCTBO ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«СЕВЕРО-КАВКАЗСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению практических занятий по дисциплине
«Математическое моделирование в задачах нефтегазовой отрасли.
Методы математической физики»
для магистров направления
130500.68 «Нефтегазовое дело»
Ставрополь, 2013
Методические указания по выполнению практических занятий по дисциплине «Математическое моделирование в задачах нефтегазовой отрасли. Методы математической физики», составлены на основании рабочего учебного плана и программы для магистров направления 130500.68 «Нефтегазовое дело».
Составитель: Коршунова Л. Г., Якушев А.В.
Содержание
Практическая занятие 1. Вывод уравнения пьезопроводности. 4
Практическое занятие 2. Приближенное решение уравнения пьезопроводности при условии постоянного дебита скважины. Расчеты P(r,t) 6
Практическое занятие 3. Параметры укрупненной модели нефтяного пласта. Определение упругого запаса. Расчеты добычи нефти и объемов внедрения воды по заданной динамике падения среднего давления. 9
Практическое занятие 4. Расчёт показателей разработки
газового месторождения. 13
Практическое занятие 5. Определение скорости потока промывочной жидкости, необходимой для очистки забоя скважины.. 17
Практическое занятие 6. Расчёт коэффициента корреляции. Определение уравнения регрессии. 18
Практическое занятие 7. Расчеты динамики падения среднего давления и объемов вторжения воды по заданной динамике отборов нефти. 21
Практическое занятие 8. Идентификация нефтяной залежи, эксплуатируемой в замкнутом упругом режиме. 24
Практическое занятие 9. Метод суперпозиций. Решение уравнения пьезопроводности по заданной динамике притока вод. 27
Практическое занятие 10. Метод суперпозиций. Решение уравнения пьезопроводности по заданной динамике падения давления на контуре укрупненой скважины.. 30
Практическое занятие 11. Сеточная модель. Элементы структуры. Вывод уравнения фильтрации однофазного флюида. 33
Практическое занятие 12. Фазовые состояния. 37
Практическое занятие 13. Математическая модель фазовых проницаемостей. 39
Практическое занятие 14. Уравнение фильтрации двух-трех фаз. 40
Практическое занятие 15. Определение основных параметров трёхфазной модели нелетучей нефти Маскета-Мереса. 43
Практическое занятие 16. Вывод уравнений неразрывности течения для трёхфазной модели нелетучей нефти Маскета-Мереса. 45
Практическое занятие 17. Многофазная многокомпонентная фильтрация. Трехфазная – двух-трехмерная фильтрация. 48
Практическая занятие 1. Вывод уравнения пьезопроводности
Пласт одноразовый, скважина в центре, поток радиально-симметричный. Жидкость слабосжимаема.
 Выделим кольцевой элемент
Выделим кольцевой элемент 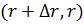 .
.
Составим расход массы жидкости через грани элемента за время 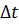 .
.
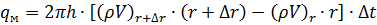
Составим изменение запаса жидкости за время 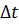 , полагая что за этот промежуток давление изменилось на
, полагая что за этот промежуток давление изменилось на 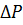 .
.
Объём элемента 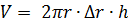 . Объём жидкости в элементе
. Объём жидкости в элементе 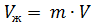 .
.
По определению коэффициента сжимаемости жидкости:
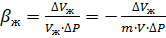 à
à 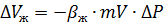
Изменение запаса жидкости в элементе 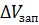 происходит за счёт изменения объёма
происходит за счёт изменения объёма 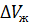 и изменения объёма скелета
и изменения объёма скелета 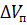 :
:
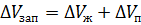
По определению, сжимаемость скелета породы:
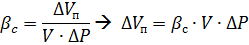
Тогда изменение запаса:
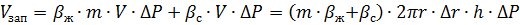 ;
; 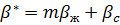
Записываем равенство 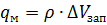 и разделим на
и разделим на  сократив множитель
сократив множитель 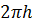
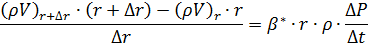
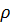 - плотность жидкости.
- плотность жидкости.
Ввиду малой сжимаемости изменениям плотности в пределах кольцевого элемента можно пренебречь и сократить в уравнении величину « 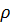 ». Переходя к пределу при
». Переходя к пределу при 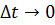 ,
, 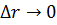 , получим уравнения неразрывности в виде:
, получим уравнения неразрывности в виде:
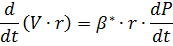
По закону Дарси 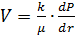 , коэффициент пьезопроводности ᴂ
, коэффициент пьезопроводности ᴂ 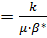 После подстановок уравнение неразрывности принимает вид:
После подстановок уравнение неразрывности принимает вид:
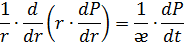
После дифференцирования в правой части уравнения неразрывности оно принимает вид, принятый под названием уравнения пьезопроводности:
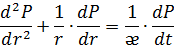
Практическое занятие 2. Приближенное решение уравнения пьезопроводности при условии постоянного дебита скважины. Расчеты P(r,t)
Теоретическая часть
Решение уравнения пьезопроводности необходимо при расчетах изменений пластовых давлений в процессе эксплуатации нефтяной скважины в нефтяном пласте, а также при расчетах изменения давлений в водоносном пласте и на контуре газовой или нефтяной залежи, эксплуатируемой как укрупненная скважина.
Дифференциальное уравнение, называется уравнением пьезопроводности, и имеет вид в декартовых координатах:
æ 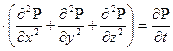 (1.1)
(1.1)
или для неустановившегося плоско-радиального течения:
æ 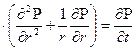 . (1.2)
. (1.2)
Получено решение этого уравнения в предложении, что пласт неограничен и введен сток (скважина) с постоянным дебитом Q.
P0 - начальное давление в невозмущенном пласте
t0=момент пуска стока
P(r,t) – давление в точке «r» пласта, в момент времени t от мгновения пуска скважины.
Основная формула упругого режима:
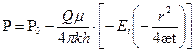 (1.3)
(1.3)
Интегральная показательная функция:
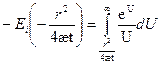 (1.4)
(1.4)
Таблица 1.1 – Значения интегральной показательной функции, х=r2/4ǽt
| х | 10-4 | 10-2 | 0.1 | ∞ | ||||
| -Ei(-x) | ∞ | 8.631 | 4.04 | 1.82 | 0.22 | 0.049 | 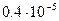 |
Основная формула упругого режима записывается в безразмерном виде, где х=r2/4ǽt
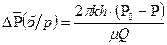 ; (1.4)
; (1.4)
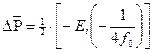
Залежь рассматривается как укрупненная скважина, пущенная в бесконечном водоносном пласте, тогда основная формула дает падение давления на контуре залежи газа Rз при постоянном дебите воды, вторгающейся в залежь.
Задача 1. Определить давление работающей залежи с дебитом воды Q в произвольной точке водоносного пласта в различных моментах времени.
Исходные данные: Q=103 м3/сут; Pнач.=100атм.; к=1 дарси; β*=10-41/атм; h=10м; µ=0,01 Па сек.
æ = 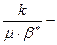 назван Щелкачевым коэффициентом пьезопроводности
назван Щелкачевым коэффициентом пьезопроводности
Найдем длину радиуса
R =70 n = 70 * 19 = 1330 м n – номер варианта, для примера n=19.
Найдем величину коэффициента: 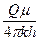 :
:
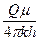 =9,2 атм
=9,2 атм
Далее: æ = = 8640 м2/сут.
Находим значения t и P для данных таблицы 1.1 t=r2/4ǽx
P вычисляется из формулы 1.3
Полученные результаты записываем в виде таблицы.
Таблица 2.1 – Результаты расчетов
| х | 10-4 | 10-2 | 0.1 | ∞ | ||||
| -Ei(-x) | ∞ | 8/631 | 4.04 | 1.82 | 0.22 | 0.049 | 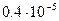 | |
| ti, сут | ∞ | 511,8 | 51,18 | 25,59 | 5,118 | |||
| Рi, атм | -∞ | 20,6 | 62,832 | 83,256 | 97,976 | 99,55 | 99,999996 |
Варианты расчетов определяются по значениям: n=1,2,3……. и т. д.
