VI Арифметическая и геометрическая прогрессии.
Применять рациональные приемы решения задач на прогрессию, как показывает практика, могут учащиеся в том случае, если они:
· отчетливо понимают введенную при изучении последовательностей символику: 
член последовательности, 
сумма n первых ее членов;
· знают не только формулы, выражающие n-ный член арифметической прогрессии через 
и d и b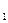 
и q для геометрической прогрессии, но и характеристические свойства арифметической и геометрической прогрессии, а также формулу 
;
· большое значение имеет использование свойств членов конечных прогрессий, равноудаленных от концов:
для арифметической прогрессии;
для геометрической прогрессии.
Например:
1. В арифметической прогрессии 
, а произведение 
. Найти прогрессию.
В данной прогрессии 10 членов, значит 
.
; 
.
Систему можно решить, используя теорему, обратную теореме Виета.
Получаем: 
и 
.
Условию задачи удовлетворяет две прогрессии:
а) 5,7,9,11,13,15,17,19,21,23.
б) 23,21,19,17,15,13,11,9,7,5.
2. Сумма второго и четвертого членов арифметической прогрессии равна 16, а произведение первого и пятого ее членов равно 28. Найти и d.
Решение этой задачи окажется более простым, если воспользоваться свойством суммы членов, равноотстоящих от концов, для прогрессии, составленной из пяти членов:
; тогда 
.
Систему можно решить устно:
.
Зная и 
, находим d: 
, d = 3 и d = -3.
Ответ: 2; 14; 3; -3;
3. Сумма трех чисел, составляющих арифметическую прогрессию, равна15. Если к ним прибавить соответственно числа 1, 4, 19, то получатся три числа, составляющие геометрическую прогрессию. Найти эти числа.
Решение:
По условию 
, так как 
, то 2 
, 
, 
. Тогда 
, 
.
По условию 
, 
, 
.
Используя характеристическое свойство геометрической прогрессии, имеем: 
:
81 = (6 – d) (24 + d), d 
+ 18d – 63 = 0, d 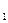= 3, d 
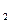= -21.
Тогда 
или 
.
Ответ: 2; 5; 8; и 26; 5; -16.
Если известна сумма трех членов, задачи можно решать таким способом:
Например:
1. Найдите сумму первых четырнадцати членов арифметической прогрессии, если 
.
Решение: в данной прогрессии 14 членов, значит а1+а14=а6+а9. S14= 
, S14=140.
А) 140.
В) 120.
С) 110.
D) 130.
Е) 100.
(Вариант-21 №23 2002г.)
2. В геометрической прогрессии пять положительных членов, первый из которых 1,5, а последний 24. Найдите знаменатель и их сумму.
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-4 №22 2002г.)
3. Сумма трех первых членов возрастающей арифметической прогрессии равна 15. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 1, то полученные три числа составят геометрическую прогрессию. Найдите сумму 10 первых членов арифметической прогрессии.
А) 120.
В) 240.
С) 360.
D) 100.
Е) 210.
(Вариант-34 №29 2003г.)
4. Сумма четвертого и шестого членов арифметической прогрессии равна 14. Найдите сумму первых десяти членов этой арифметической прогрессии.
А) 14.
В) 63.
С) 126.
D) 56.
Е) 64.
(Вариант-28 №29 2003г.)
5. В арифметической прогрессии 
Найдите 
и .
А) d = 3.6; = -5.7.
В) d = 1.4; = 3.1.
С) d = 1.6; = 2.3.
D) d = 1.2; = 3.1.
Е) d = 1.2; = 3.9.
(Вариант-19 №12 2004г.)
6. Числа a, b, c составляют арифметическую прогрессию с разностью d = 4. Найдите числа a, b, c, если a, b, c + 8 последовательные члены геометрической прогрессии.
А) a = 5, b = 9, c = 13.
В) a = 3, b = 7, c = 11.
С) a = 2, b = 6, c = 10.
D) a = 1, b = 5, c = 9.
Е) a = 6, b = 10, c = 14.
(Вариант-27 №12 2004г.)
7. Найдите знаменатель геометрической прогрессии, если b 
= 25, b 
= 16.
А) 
.
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-30 №12 2004г.)
8. Найдите значения х, при которых числа х – 4, 
, х – 6 образуют арифметическую прогрессию.
А) 5.
В) 4.
С) -7.
D) 3.
Е) 7.
(Вариант-11 №12 2004г.)
9. Найдите знаменатель геометрической прогрессии, если b 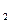= 27, b = 3.
А) .
В) 
.
С) 
.
D) 
.
Е) 
.
(Вариант-10 №12 2004г.)
10. Три числа образуют возрастающую геометрическую прогрессию. Если среднее из них удвоить, то получится арифметическая прогрессия. Найдите знаменатель прогрессии.
А) 2.
В) 2 -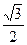 
.
С) 2 +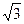 
.
D) 2 +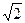 
.
Е) 2 - .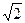
(Вариант-33 №30 2005г.)
11. Сумма четвертого и шестого членов арифметической прогрессии равна 14. Найдите сумму первых девяти членов этой арифметической прогрессии.
А) 126.
В) 14.
С) 56.
D) 63.
Е) 64.
(Вариант-22 №6 2005г.)
12. В арифметической прогрессии 
. Найдите и d.
А) d = 2; = -6.
В) d = 3; = 6.
С) d = 2; = 6.
D) d = -6; = 3.
Е) d = 6; = 3.
(Вариант-3 №18 2006г.)
Коды правильных ответов
| A | C | A | B | E | C | B | E | D | C | D | B |