IV. Использование геометрического смысла модуля при решении уравнений и неравенств, содержащих знак модуля.
При решении простейших неравенств, уравнений, содержащих неизвестное под знаком модуля, можно использовать геометрический смысл модуля.
Абсолютную величину (модуль) действительного числа х, т.е. |x|, можно геометрически истолковать, как расстояние от точки, изображающей число х, до начала отсчета; |x - а| означает расстояние между точками х и а на числовой прямой.
Например, если |x| = 3, то на числовой оси имеются только две точки 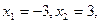 которые удалены от начала отсчёта 0 на расстояние, равное трем.
которые удалены от начала отсчёта 0 на расстояние, равное трем.


 -3 0 3
-3 0 3


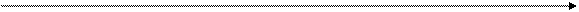
 х
х
Примеры:
1. Решите уравнение: |x - 1| = 3.
Уравнению удовлетворяют такие точки х, расстояние которых от 1 на числовой прямой равно трём.


 -2 1 4
-2 1 4


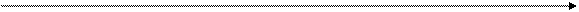
 х
х
Это точки -2 и 4.
Ответ: 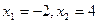 .
.
(Вариант-23 №6 2005г.)
2. Решите уравнение: |2x - 3| = 5. разделим обе части уравнения на 2:
|x – 1,5| = 2,5
От точки 1,5 отложим влево и вправо 2,5 единицы, получим точки 4 и – 1.


 -1 1,5 4
-1 1,5 4


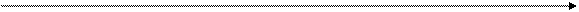
 х
х
Ответ: 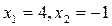 .
.
3. Решите неравенство: |х - 3| < 1.
Геометрический способ решения.
Неравенству удовлетворяют такие точки, которые удалены от точки 3 на расстояние, меньшее 1. От точки 3 отложим влево и вправо единицу, получим две точки: 2 и 4.


 2 3 4
2 3 4


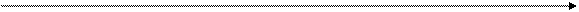
 х
х
Точки, расстояние до которых от точки 3 меньше единицы, находятся внутри интервала (2;4). 2 и 4 в решение не входят, т.к. неравенство строгое. Поэтому, решением будет интервал (2;4).
Ответ: х 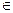 (2; 4)
(2; 4)
4. Решите неравенство: |2х + 3| < 5.
Разделим обе части неравенства на 2: 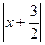 <
< 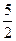 или |x – (-
или |x – (- 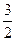 )| <
)| < 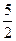 .
.
От точки - 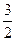 откладываем
откладываем 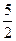 влево и вправо. Получаем точки -4 и 1.
влево и вправо. Получаем точки -4 и 1.


 -4 -3/2 1
-4 -3/2 1


 х
х
И таким образом получаем решение (-4; 1).
Ответ: (-4; 1).
5. Решите неравенство: |2х - 3| > 7.
Разделим обе части неравенства на 2: |x – 1,5| > 3,5
От точки 1,5 отложим влево и вправо 3,5 единиц. Получаем точки -2 и 5. точки, удалённые от 1,5 на расстояние, большее 3,5 единицам, расположены левее -2 и правее 5. Поэтому, решением неравенства будет объединение интервалов 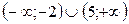 . Т.к. неравенство строгое, -2 и 5 не принадлежат данным промежуткам.
. Т.к. неравенство строгое, -2 и 5 не принадлежат данным промежуткам.


 -2 1,5 5
-2 1,5 5


 х
х
Ответ: 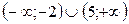 .
.
Геометрический способ решения можно применить при решении следующих заданий:
1. Решите уравнение: |2x - 3| = 6.
А) (- 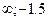 ).
).
В) (-4.5; 4.5).
С) (-4.5; 1.5).
D) (- 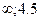 ).
).
Е) (-1.5; 4.5).
(Вариант-18 №20 2005г.)
2. Определите верный промежуток-решение неравенства: |2x - 3| < 5.
(Вариант-16 №20 2005г.)
3. Решите уравнение: |2x - 3| = 1.
А) {2; -1}.
В) {-2; -1}.
С) {2; 1}.
D) {-2; 1}.
Е) {-3; 1}.
(Вариант-3 №12 2005г.)
4. Решите неравенство: |3х - 1| 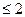 .
.
А) -1\3 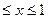 .
.
В) -3 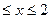 .
.
С) все ответы неверны.
D) -1 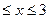 .
.
Е) -1\2 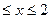 .
.
(Вариант-34 №18 2007г.)
5. Определите верное решение неравенства: |x - 1| 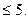
А) [4; 6].
В) (-  ; 4].
; 4].
С) [-6; 4].
D) (-  ; -4].
; -4].
Е) [-4; 6].
(Вариант-23 №8 2007г.)
6. Определите верное решение неравенства: |x + 2| 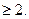
А) [0; +  ).
).
В) (-  ; 0)
; 0) 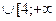 ).
).
С) [-4; 0].
D) (-  ; -4].
; -4].
Е) [-  ; -4]
; -4] 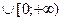
(Вариант-22 №8 2007г.)
7. Определите верное решение неравенства: |1 + 2x| > 1.
А) (0;1).
В) (-  ; -1)
; -1) 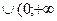 ).
).
С) (-  ; 0)
; 0) 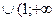 ).
).
D) (-1; +  ).
).
Е) (-1; 0)
(Вариант-16 №19 2007г.)
8. Решите неравенство: |х| 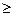 1.
1.
А) (1; +  ).
).
В) (-  ; -1).
; -1).
С) (0; +  ).
).
D) (-1; 1).
Е) (-  ; -1]
; -1] 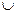 [1; +
[1; +  ).
).
(Вариант-5 №7 2007г.)
9. Определите верный промежуток-решение неравенства: |3 + x| 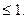
(Вариант-14 №7 2004г.)
10. Решите уравнение: |x - 1| =3.
A) {4; -2}.
B) {-1; 4}.
C) {2; -4}.
D) {-4; 3}.
E) {0; -3}.
(Вариант-17 №4 2004г.)
11. Определите верный промежуток-решение неравенства: |2x - 3| < 5.
(Вариант-23 №8 2004г.)
12. Решите систему уравнений: 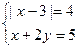
А) (0; 5),(-2;8).
В) (-1; 3), (7; -1).
С) (-1; -3), (-5; 1).
D) (1; -3), (-5; -1).
Е) (-1; 0) (5; 0).
(Вариант-11 №25 2006г.)
13. Решите неравенство: 2|х - 1| 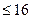 .
.
А) [-8; 9].
В) (- 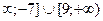 .
.
С) [-7; 9].
D) (- 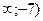 .
.
Е) [9; + 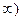 .
.
(Вариант-19 №4 2003г.)
14. Решите неравенство: |х| <3.
А) (3; +  ).
).
В) (-  ; -3)
; -3) 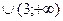 .
.
С) (-3; 3).
D) (-3; 3].
Е) (-  ; 3).
; 3).
(Вариант-21 №4 2003г.)
Коды правильных ответов
| E | C | C | A | E | E | B | E | E | A | E | B | C | C |
