При решении ряда систем двух уравнений с двумя переменными можно применять теорему, обратную теореме Виета.
Например:
1. Решите систему уравнений 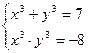
Чаще всего эту систему решают способом подстановки. Но её можно решить более рациональным путём. Из условия следует, что 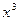 и
и 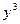 являются корнями некоторого приведенного квадратного уравнения
являются корнями некоторого приведенного квадратного уравнения 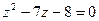 . Корни этого уравнения 8 и -1.
. Корни этого уравнения 8 и -1.
Получаем: 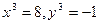
х = 2, у = -1.
или: 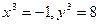
х = -1, у = 2.
Ответ: (2; -1), (-1; 2).
2. Решите систему уравнений 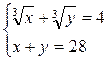
Возведем в куб обе части первого уравнения:
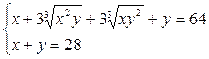
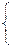
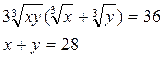 ,
, 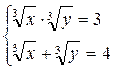
Используя теорему, обратную теореме Виета, получаем 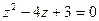 .
.
Корни этого уравнения 3 и 1.
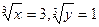
х = 27, у = 1
или:
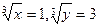
х = 1, у = 27
Ответ: (27; 1), (1; 27).
Этот метод можно применять при решении систем в тестах:
1. Решите систему уравнений 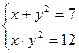
Решение:
Из условия следует, что х и у2 являются корнями некоторого приведённого квадратного уравнения а2 -7а +12 =0. Корни этого уравнения 3 и 4. Получаем: х=3, у2=4, у=±2, или х=4, у2=3, у = ± 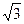 .
.
А) (5; 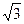 ), (5; -
), (5; - 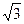 ), (3; 2), (3; -2).
), (3; 2), (3; -2).
В) (4; 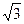 ), (4; -
), (4; - 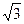 ), (3; 2), (3; -2).
), (3; 2), (3; -2).
С) (3; 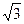 ), (3; -
), (3; - 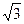 ), (3; 2), (3; -2).
), (3; 2), (3; -2).
D) (2; 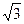 ), (2; -
), (2; - 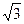 ), (3; 2), (3; -2).
), (3; 2), (3; -2).
Е) (5; 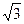 ), (3; -
), (3; - 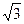 ), (3; 2), (3; -2).
), (3; 2), (3; -2).
(Вариант-23 №24 2003г.)
2. Решите систему уравнений 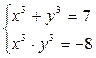
А) (-1; 2), (2; -1).
В) (-1; 3), (1; -1).
С) (-2; 1), (-1; 2).
D) (2; 1), (-1; -2).
Е) (2; -1), (-1, 1).
(Вариант-8 №27 2003г.)
(Вариант-13 №26 2007г.)
(Вариант-25 №27 2006г.)
3. Решите систему уравнений 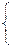
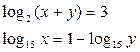
Указание к решению: переходим к системе уравнений 
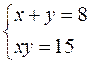 .
.
А) (1; 1).
В) (3; 5), (5; 3).
С) (15;3), (3;15).
D) (-3; -5), (-5; -3).
Е) нет решения.
(Вариант-13 №15 2004г.)
4. Решите систему уравнений 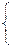
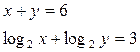
А) (5; 1), (1; 5).
В) (2; 4), (4; 2).
С) (0; 6).
D) (3; 3).
Е) (6; 0).
(Вариант-25 №15 2004г.)
(Вариант-14 №20 2005г.)
5. Решите систему уравнений 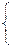
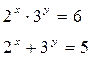
А) (2; 0).
В) (1; 1); ( 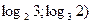 .
.
С) (-1; 1).
D) (-1; 1); ( 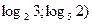 .
.
Е) (-1; 0).
(Вариант-21 №25 2005г.)
(Вариант-15 №26 2006г.)
Коды правильных ответов
| B | A | B | B | B |
При решении квадратных неравенств (и неравенств, сводящихся к ним), с которыми приходится часто иметь дело при подготовке к ЕНТ, удобно пользоваться свойством квадратного трехчлена 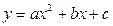 , сформулированного следующим образом: «Если корни квадратного трехчлена действительные числа, то квадратный трехчлен имеет знак коэффициента при
, сформулированного следующим образом: «Если корни квадратного трехчлена действительные числа, то квадратный трехчлен имеет знак коэффициента при 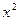 на всей числовой оси, за исключением замкнутого интервала между его корнями -
на всей числовой оси, за исключением замкнутого интервала между его корнями - 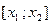 , обращается в нуль в концах этого интервала, а внутри этого интервала знак квадратного трехчлена противоположен знаку коэффициента при
, обращается в нуль в концах этого интервала, а внутри этого интервала знак квадратного трехчлена противоположен знаку коэффициента при 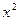 ». Это свойство можно использовать при решении неравенств:
». Это свойство можно использовать при решении неравенств:
1. Решите неравенство: 5 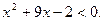
Решение: 5х2+9х-2=0, х1=-2, х2= 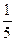 . Так как квадратный трёхчлен имеет различные корни, то знак квадратного трёхчлена совпадает со знаком коэффициента а (а=5>0) во всех точках промежутков ( -
. Так как квадратный трёхчлен имеет различные корни, то знак квадратного трёхчлена совпадает со знаком коэффициента а (а=5>0) во всех точках промежутков ( -  ; -2) и (
; -2) и ( 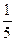 ;
;  ), и противоположен знаку коэффициента а во всех точках промежутка ( -2;
), и противоположен знаку коэффициента а во всех точках промежутка ( -2; 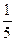 ).
).
Ответ: х 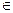 (-2;
(-2; 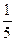 ).
).
А) (-2; 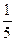 ).
).
В) ( 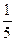 ; 2).
; 2).
С) (- 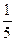 ;
; 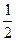 ).
).
D) (-2; 5) .
Е) (- 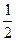 ;
; 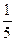 ).
).
(Вариант-23 №8 2006г.)
2. Решите неравенство: 7 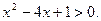
А) (-  ; -
; - 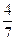 ).
).
В) ( 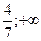 ).
).
С) (- 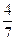 ;
; 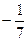 ).
).
D) (- 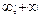 ) .
) .
Е) ( 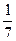 ;
; 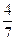 ).
).
(Вариант-34 №8 2004г.)
3. Решите неравенство: 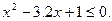
А) (-  ;3,2).
;3,2).
В) ( 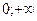 ).
).
С) (- 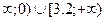 .
.
D) (- 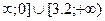 .
.
Е) (0; 3,2).
(Вариант-12 №8 2007г.)
4. Определите верное решение неравенства: 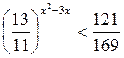
Ответ: 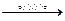
1 2 х
(Вариант-14 №18 2007г.)
5. Определите верное решение неравенства: 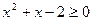 .
.
А) [-2; 1].
В) [-1; 2].
С) 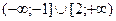 .
.
D) 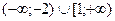 .
.
Е) 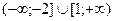 .
.
(Вариант-15 №18 2007г.)
6. Решите неравенство: 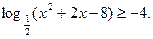
А) (-  ; -4)
; -4) 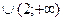 .
.
В) 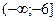
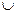 [
[ 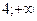 ).
).
С) [-6; -4) 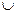 (2; 4].
(2; 4].
D) [-6;4].
Е) (-4; 2).
(Вариант-6 №18 2007г.)
7. Решите неравенство: 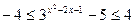 .
.
А) нет решений.
В) [3;  ).
).
С) (-1; 1 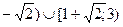 .
.
D) [-1; 1 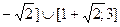 .
.
Е) [-1; 3].
(Вариант-9 №18 2005г.)
8. Решите неравенство: 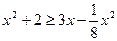 .
.
А) 2.
В) 1\2.
С) (1; 6).
D) 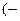
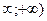 .
.
Е) 1.
(Вариант-12 №19 2005г.)
Коды правильных ответов
| A | D | E | D | E | C | D | D |
III. Метод Крамера.
Системы линейных уравнений с двумя неизвестными можно решать методом подстановки, методом сложения, а можно применять метод Крамера или метод определителей. Учащимся, интересующимся математикой, этот метод нравится, и они его используют при подготовке к ЕНТ.
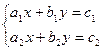
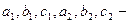 некоторые числа
некоторые числа
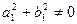 ,
, 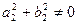
По коэффициентам системы составляются три определителя:
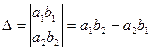
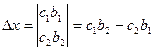
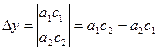
1) Если 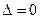 , а
, а 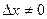 или
или 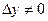 , то система не имеет решений.
, то система не имеет решений.
2) Если 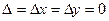 , то система имеет бесконечное множество решений.
, то система имеет бесконечное множество решений.
3) Если 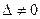 , то система имеет единственное решение:
, то система имеет единственное решение: 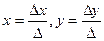 .
.
Например:
Решите систему уравнений 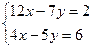
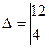
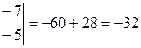
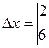
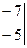 = -10 + 42 = 32
= -10 + 42 = 32
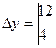
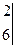 = 72 - 8 = 64
= 72 - 8 = 64
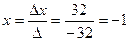 , у =
, у = 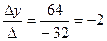
Ответ: (-1; -2).
Этим методом можно решить системы:
1. Решите систему уравнений: 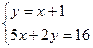
А) (-1; 0).
В) (2; 3).
С) (-2; -1).
D) (6; 7).
Е) (4; 5).
(Вариант-19 №5 2003г.)
2. Решите систему уравнений: 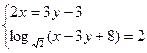
Указание к решению: от данной системы переходим к системе 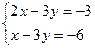 .
.
А) (3; 3).
В) (7; 8).
С) (-3; -1).
D) (-3; -3).
Е) (-1; 3).
(Вариант-26 №24 2003г.)
3. Решите систему уравнений: 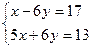
А) (-13; -5).
В) (-1; -3).
С) (-7; -4).
D) (5; -2).
Е) (11; -1).
(Вариант-19, №15, 2004г.)
4. Решите систему уравнений: 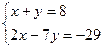
А) (-3; 5).
В) (5; 3).
С) (-5; -3).
D) (3; 5).
Е) (3; -5).
(Вариант-24, №15, 2004г.)
5. Решите систему уравнений: 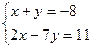
А) (-5; -3).
В) (-3; 5).
С) (5; 3).
D) (3; 5).
Е) (3; -5).
(Вариант-2, №6, 2005г.)
6. Решите систему уравнений: 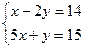
А) (2; -7).
В) (7; 2).
С) (5; 0).
D) (0; 4).
Е) (4; -5).
(Вариант-26, №6, 2005г.)
7. Решите систему уравнений: 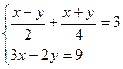
А) (1; 7).
В) (-6; 0).
С) (5; 3).
D) (0; 6).
Е) (-5; 3).
(Вариант-23, №19, 2007г.)
8. Решите систему уравнений: 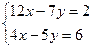
А) (2; 4).
В) (1\6; 0).
С) (-2; -1).
D) (4; 2).
Е) (-1; -2).
(Вариант-15, №14, 2004г.)
Коды правильных ответов
| B | A | D | D | A | E | C | E |
