Применение общего интеграла к решению некоторых задач
Применение общего интеграла к решению некоторых задач
Математической физики
Задано волновое уравнение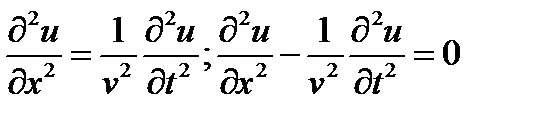 
обозначим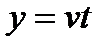 
уравнение примет вид: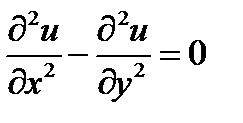 
общий интеграл волнового уравнения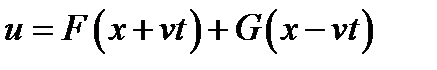 
волна распространяющаяся вправо от начала координат-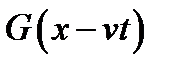 
волна распространяющаяся влево от начала координат-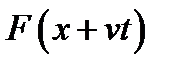 
Рассмотрим трехмерное волновое уравнение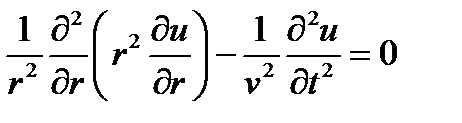 
предположим инвариантность решения от угловых координат θ и φ
замена переменной u=w/r
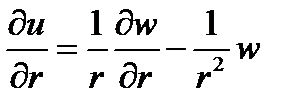
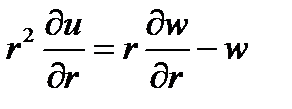
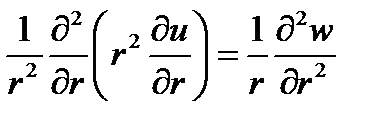
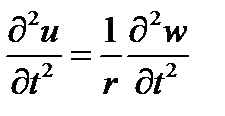
в результате получим уравнение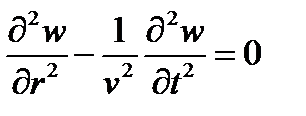 
общий интеграл волнового уравнения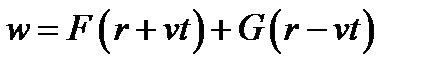 
волна распространяющаяся из бесконечности в точку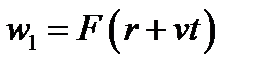 
волна распространяющаяся из точки в бесконечность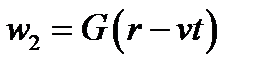 
получим окончательно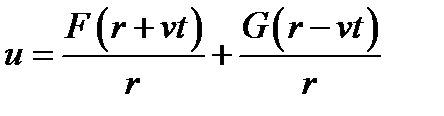 
.
Функция Грина оператора Штурма — Лиувилля (одномерный случай)
Постановка задачи
Пусть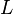 
— оператор Штурма — Лиувилля, линейный дифференциальный оператор вида
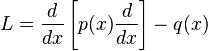
и пусть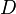 
— оператор краевых условий
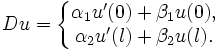
Пусть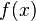 
— непрерывная функция на промежутке 
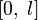. Предположим также, что задача
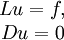
регулярна, то есть существует только тривиальное решение однородной задачи.
Теорема Грина
Тогда существует единственное решение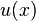 
, удовлетворяющее системе
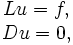
которое задаётся выражением
,
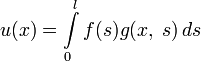где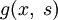 
— функция Грина, которая удовлетворяет следующим требованиям (они же — свойства функции Грина):
1. 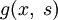непрерывна по 
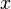и 
.
2. Для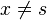 
, 
.
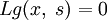3. Для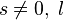 
, 
.
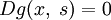4. Скачок производной: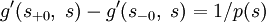 
.
5. Симметрична: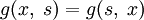 
.
Нахождение функции Грина
В виде ряда через собственные функции оператора
Если множество собственных векторов (собственных функций)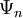 
дифференциального оператора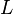
(то есть набор функций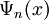 
, таких, что для каждой найдётся число 
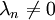, что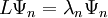 
)
полно, то можно построить функцию Грина с помощью собственных векторов 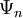и собственных значений 
.
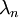Под полнотой системы функций 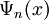подразумевается выполнение соотношения:
.
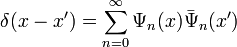Можно показать, что
.
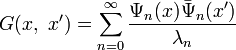Действительно, подействовав оператором 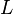на эту сумму, мы получим дельта-функцию (в силу соотношения полноты).
(Чертой сверху обозначено комплексное сопряжение, если 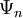— вещественные функции, его можно не делать).
Функции Бесселя и Вебера. Рекуррентные соотношения для функций Бесселя.
Функции Бесселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:
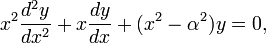
где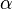 
— произвольное комплексное число, называемое порядком.
Наиболее часто используемые функции Бесселя — функции целых и полуцелых порядков.
Хотя 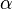и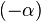 
порождают одинаковые уравнения для вещественных 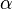, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по ).
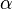Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.
Гипергеометрический ряд
Функции Бесселя могут быть выражены через гипергеометрическую функцию:
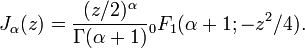
Таким образом, при целых 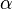функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.
Производящая функция
Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно
.
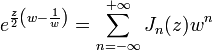Применение общего интеграла к решению некоторых задач
Математической физики
Задано волновое уравнение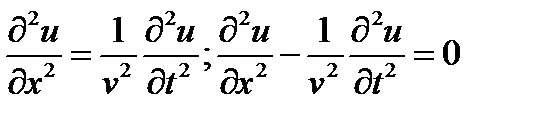
обозначим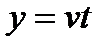
уравнение примет вид: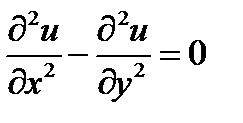
общий интеграл волнового уравнения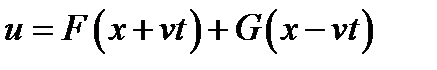
волна распространяющаяся вправо от начала координат-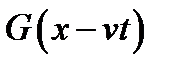
волна распространяющаяся влево от начала координат-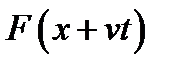
Рассмотрим трехмерное волновое уравнение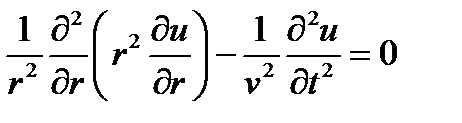
предположим инвариантность решения от угловых координат θ и φ
замена переменной u=w/r
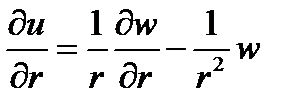
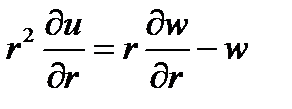
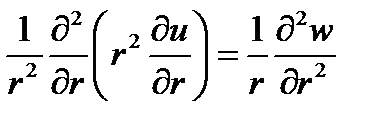
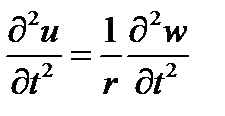
в результате получим уравнение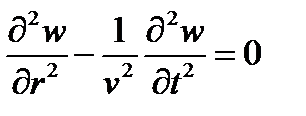
общий интеграл волнового уравнения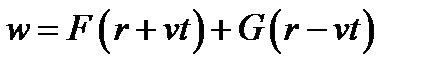
волна распространяющаяся из бесконечности в точку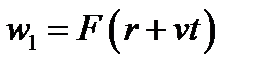
волна распространяющаяся из точки в бесконечность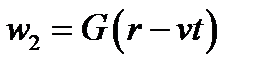
получим окончательно 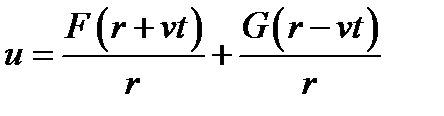.