Алгоритм решения задач на проценты.

Нахождение процентов от числа.
I способ 1. Найти сколько приходится на 1 % (отвара, торта, яблок, зверей и т.д.), для этого разделить данное число на 100. 2. Умножить найденное число на данное количество процентов	Задача На планете Железяка работают 890 роботов. 70% из них пострадали от лже-профессора Верховцева. Сколько роботов вышло из строя? 890 р. – 100% ? р. - 70% Решение : 1) 890 : 100 = 8,9(р) – 1% 2) 8,9 · 70 = 623(р) – 70% Ответ: 623робота вышло из строя.
II способ 1. Перевести проценты в десятичную дробь, для этого разделить количество процентов на 100. 2. Умножить данное число на эту десятичную дробь.	Задача На планете Железяка работают 890 роботов. 70% из них пострадали от лже-профессора Верховцева. Сколько роботов вышло из строя? Решение: 70% = 0,7 890 · 0,7 = 623 (р) – 70% Ответ: 623робота вышло из строя.
Нахождение числа по его процентам.
I способ Найти сколько приходится на 1 %,то есть нужно разделить данное в задаче число на соответствующее число процентов. Умножить найденное число на 100.	Задача Экспедиция профессора Селезнева нашла для зоопарка 12 редких животных, что составило 15% всех обитателей зоопарка. Сколько всего зверей в зоопарке? 12 зв. – 15% ? зв. – 100% Решение: 1) 12 : 15 = 0.8 (зв.) – 1% 2) 0,8 · 100 = 80 (зв.) – 100% Ответ: всего в зоопарке 80 зверей.
II способ 1. Перевести проценты в десятичную дробь, для этого разделить количество процентов на 100. 2. Разделить данное число на эту десятичную дробь.	Задача Экспедиция профессора Селезнева нашла для зоопарка 12 редких животных, что составило 15% всех обитателей зоопарка. Сколько всего зверей в зоопарке? Решение: 15% = 0,15 12 · 0,15 = 80 (зв.) – 100% Ответ: всего в зоопарке 80 зверей.
Нахождение процентного отношения.
Найти сумму всех составляющих(животных, деревьев и т.д.) Найти какую часть составляет искомое от целого( девочки от всего класса, груши от всех деревьев) Вырази дробь в виде процентов, для этого умножить полученную дробь на 100%.	Задача В классе у Алисы учится 12 девочек и 13 мальчиков. Сколько процентов всех учащихся составляют девочки? Решение: 1) 12 + 13 = 25 (уч.) – всего в классе 2) 12 : 25 = 0,48 – такую часть составляют девочки 3) 0,48 · 100% = 48 % Ответ: девочки составляют 48% .

Задачи на вероятность

Прежде, чем мы начнем решать задачи, давайте-ка освежим знания по теории вероятностей.

Для чего же нужна теория вероятностей? Дело в том, что вся наша жизнь состоит из событий, которые случаются с нами или нет. Это хорошие и плохие события – неважно, какие они, важно то, произошли они, или нет, произойдут, или минуют. Поскольку мы не знаем, случится событие или нет – мы называем его случайным. Как оценить шансы события на то, что оно все-таки произойдет – это задача теории вероятности.

События, которые никогда не произойдут – это события невозможные. Например, вероятность того, что Земля без причин изменит направление своего вращения вокруг Солнца – очевидно, равна нулю. Или что число дней в следующем месяце будет равно 32. Или выпадение 7 при бросании игрального кубика.

События, которые точно произойдут, называются достоверными. Их вероятность равна 1 – например, вероятность наступления зимы, по крайней мере, календарной.

Случайное событие, как мы уже сказали, может произойти, а может не произойти. Частотой такого события называется отношение удачных опытов (таких, в которых событие произошло) к числу всех проведенных опытов. Исходы таких опытов называют элементарными исходами, которые могут включать благоприятные исходы – такие, в которых событие произошло. Чем больше проведенных опытов, тем ближе частота к вероятности. То есть, если опыт был проведен достаточно много раз, то можем считать, что вероятность события равна его частоте.

При решении задач на подкидывание обратите внимание на следующее:

для монеты число всевозможных исходов определяется как 2ⁿ , где n-число подкидываний, Для кубика число всевозможных исходов определяется как 6ⁿ , где n-число подкидываний

1. На та­рел­ке лежат пи­рож­ки, оди­на­ко­вые на вид: 4 с мясом, 1 с ка­пу­стой и 3 с яб­ло­ка­ми. Петя на­у­гад вы­би­ра­ет один пи­ро­жок. Най­ди­те ве­ро­ят­ность того, что пи­ро­жок ока­жет­ся с яб­ло­ка­ми.

Всего пирожков 8, то есть Петя может выбрать любой – один из восьми. Тогда элементарных исходов – 8. Благоприятных исходов всего 3 – ведь пирожков с яблоками три на тарелке. Тогда вероятность такого выбора равна 3/8. Задача решена, однако, ответ надо записать в бланк. Для этого его надо представить десятичном виде – в виде дроби с основанием 10, 100, 1000 и т.д. Как это сделать в данном случае? Чтобы получить в основании 100, разделим на 2 всю дробь и умножим на 25: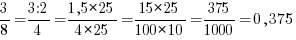

Ответ: 0,375

2.В лыж­ных гон­ках участ­ву­ют 13 спортс­ме­нов из Рос­сии, 2 спортс­ме­на из Нор­ве­гии и 5 спортс­ме­нов из Шве­ции. По­ря­док, в ко­то­ром спортс­ме­ны стар­ту­ют, опре­де­ля­ет­ся жре­би­ем. Най­ди­те ве­ро­ят­ность того, что пер­вым будет стар­то­вать спортс­мен не из Рос­сии.

Кому-то первым стартовать придется, это может быть любой из спортсменов. То есть всего исходов столько, сколько всего спортсменов – 20. Благоприятны нашему событию такие, когда стартовать первым будет не россиянин – а не россиян всего 7. Иными словами, вероятность, что первым будет не россиянин – 7/20. Представим результат в виде десятичной дроби: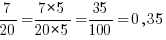

Ответ: 0,35

3.Петя, Катя, Ваня, Даша и На­та­ша бро­си­ли жре­бий, кому на­чи­нать игру. Най­ди­те ве­ро­ят­ность того, что на­чи­нать игру дол­жен будет маль­чик.

Элементарных исходов столько, сколько всего игроков – пять. Из них мальчиков двое, благоприятных исходов – два из пяти. Вероятность равна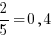

Ответ: 0,4

4.Коля вы­би­ра­ет трех­знач­ное число. Най­ди­те ве­ро­ят­ность того, что оно де­лит­ся на 5.

Сначала посчитаем, сколько у нас всего трехзначных чисел: из тысячи отбрасываем 99 первых, и последнее, 1000 – четырехзначное число. Тогда имеем 900 трехзначных чисел. на 5 делится каждое пятое: 900/5= 180. Проверим результат. Имеем алгебраическую прогрессию со знаменателем d=5. Первый член прогрессии – 100. Последний – 995. Определим число членов с помощью формулы n-ного члена:

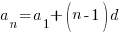, откуда 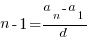, тогда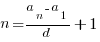

Считаем: .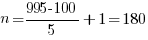

Ну и осталось определить вероятность: благоприятных исходов 180, а всего 900: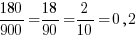

Ответ: 0,2

5.В каж­дой де­ся­той банке кофе со­глас­но усло­ви­ям акции есть приз. Призы рас­пре­де­ле­ны по бан­кам слу­чай­но. Варя по­ку­па­ет банку кофе в на­деж­де вы­иг­рать приз. Най­ди­те ве­ро­ят­ность того, что Варя не най­дет приз в своей банке.

Данная задача – на противоположные события. Некоторые события могут образовывать пары “случилось – не случилось”. Так как одно событие из пары произойдет обязательно, то вероятность пары событий равна 1. Если событие А – “случилось” – то противоположное ему событие В – “не случилось”. Тогда вероятность события В равна 1 – А.

Раз приз в каждой 1-й банке, значит, вероятность выиграть его – 1/10. Тогда вероятность не выиграть: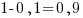

Ответ: 0,9

6.В сред­нем на 50 исправных фо­на­ри­ков при­хо­дит­ся два не­ис­прав­ных. Най­ди­те ве­ро­ят­ность ку­пить ра­бо­та­ю­щий фо­на­рик.

Ре­зуль­тат округ­ли­те до сотых.

Итак, здесь важно не ошибиться. Если на 50 работающих фонариков с одной стороны приходится 2 неработающих, то всего фонариков – 52! Это тонкость этой задачи. Вероятность купить работающий фонарик равна 50/52, и к сожалению, придется считать в столбик, чтобы дать правильный ответ: 0,9615. Округляем до сотых:

Ответ: 0,96

7.В мешке со­дер­жат­ся же­то­ны с но­ме­ра­ми от 2 до 51 вклю­чи­тель­но. Ка­ко­ва ве­ро­ят­ность, того, что номер из­вле­чен­но­го на­у­гад из мешка же­то­на яв­ля­ет­ся од­но­знач­ным чис­лом?

Всего жетонов в мешке – 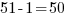. Однозначных номеров 8 штук: 2, 3, 4, 5, 6, 7, 8, 9. Значит, благоприятных исходов 8 из 50. Тогда вероятность равна 8/50 или 16/100.

Ответ: 0,16.

8.Перед на­ча­лом фут­боль­но­го матча судья бро­са­ет мо­нет­ку, чтобы опре­де­лить, какая из ко­манд будет пер­вой вла­деть мячом. Ко­ман­да А долж­на сыг­рать два матча — с ко­ман­дой В и с ко­ман­дой С. Най­ди­те ве­ро­ят­ность того, что в обоих мат­чах пер­вой мячом будет вла­деть ко­ман­да А.

Всего у монетки 2 стороны – то есть имеем два исхода для первого матча, и два исхода для второго. То есть четыре. Составим дерево: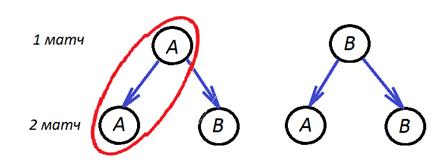

Видим, что изо всех исходов (из 4) нас устраивает единственный. Тогда вероятность равна 1/4, или 0,25.

Ответ: 0,25

9.На каж­дые 1000 элек­три­че­ских лам­по­чек при­хо­дит­ся 5 бра­ко­ван­ных. Ка­ко­ва ве­ро­ят­ность ку­пить ис­прав­ную лам­поч­ку?

В от­ве­те ука­жи­те ре­зуль­тат, округ­лен­ный до ты­сяч­ных.

Здесь такая же хитрость, как и в задаче про фонарики: всего лампочек у нас 1005: 1000 работают, и 5 – нет. Вероятность купить исправную лампу равна 1000/1005. Осталось это посчитать: 0,99502.

Не забудем округлить до тысячных: 0,995

Ответ: 0,995.

Пример 4. Когда подбрасываем монету, какова вероятность выпадения решки?
Исходов 2 – орел или решка. (считается, что монета никогда не падает на ребро) Благоприятный исход – решка, 1.
Вероятность 1/2=0,5
Ответ: 0,5.

Пример 5. А если подбрасываем монету два раза? Какова вероятность того, что оба раза выпадет орел?
Главное определить, какие элементарные исходы будем рассматривать при подбрасывании двух монет. После подбрасывания двух монет может получиться один из следующих результатов:
1) PP – оба раза выпала решка
2) PO – первый раз решка, второй раз орел
3) OP – первый раз орел, второй раз решка
4) OO – оба раза выпал орел
Других вариантов нет. Значит, элементарных исходов 4. Благоприятный из них только первый, 1.
Вероятность: 1/4=0,25
Ответ: 0,25

Какова вероятность того, что из двух подбрасываний монеты один раз выпадет решка?
Количество элементарных исходов то же, 4. Благоприятные исходы – второй и третий, 2.
Вероятность выпадения одной решки: 2/4=0,5

В таких задачах может пригодиться ещё одна формула.
Если при одном бросании монеты возможных вариантов результата у нас 2, то для двух бросаний результатов будет 2·2=2²=4 (как в примере 5), для трех бросаний 2·2·2=2³=8, для четырех: 2·2·2·2=2⁴=16, … для N бросаний возможных результатов будет 2·2·...·2=2^N.

Так, можно найти вероятность выпадения 5 решек из 5 бросаний монеты.
Общее число элементарных исходов: 2⁵=32.
Благоприятных исходов: 1. (РРРРР – все 5 раз решка)
Вероятность: 1/32=0,03125

То же верно и для игральной кости. При одном бросании возможных результатов здесь 6. Значит, для двух бросаний: 6·6=36, для трех 6·6·6=216, и т. д.

Пример 6. Бросаем игральную кость. Какова вероятность, что выпадет четное число?

Всего исходов: 6, по числу граней.
Благоприятных: 3 исхода. (2, 4, 6)
Вероятность: 3/6=0,5

Пример 7. Бросаем две игральные кости. Какова вероятность, что в сумме выпадет 10? (округлить до сотых)

Для одного кубика 6 возможных исходов. Значит, для двух, по вышеупомянутому правилу, 6·6=36.
Какие исходы будут благоприятными для того, чтоб в сумме выпало 10?
10 надо разложить на сумму двух чисел от 1 до 6. Это можно сделать двумя способами: 10=6+4 и 10=5+5. Значит, для кубиков возможны варианты:
(6 на первом и 4 на втором)
(4 на первом и 6 на втором)
(5 на первом и 5 на втором)
Итого, 3 варианта. Искомая вероятность: 3/36=1/12=0,08
Ответ: 0,08