Условия уравновешенности механизма

Условия уравновешенности механизмов в общем виде можно охарактеризовать уравнениями

,

,

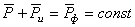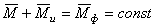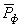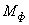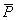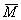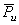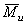где и – главный вектор сил и главный момент сил давления станины механизма на фундамент, опору; и – главный вектор сил и главный момент всех других сил, внешних по отношению к механизму; и – главный вектор сил инерции и главный момент сил инерции звеньев механизма.

С достаточной для практики точностью часто ограничиваются условиями

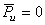, (11)

.

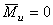Этого можно достичь установкой противовесов на подвижных звеньях, рациональным размещением центров масс звеньев механизма при его проектировании.

Статическое уравновешивание плоского механизма с помощью противовесов

Часто ограничиваются лишь статическим уравновешиванием механизма и его звеньев, т.е. выполнением условия (11) 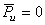. Это условие соответствует постоянству положения центров масс звеньев относительно стойки (т.е. центр их масс должен быть неподвижен). Так как 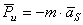, , 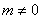то необходимо обеспечить условие 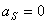, т.е. ускорение центра тяжести должно отсутствовать.

Рассмотрим последовательность статического уравновешивания на примере четырёхшарнирного механизма (рис. 6.4, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причём в силу неподвижности точек A и D, массы, сосредоточенные в этих точках, можно не учитывать.

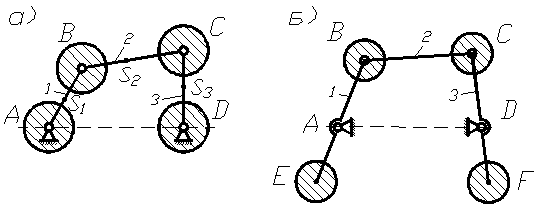
Рис. 6.4

Приведённые массы в точках В и С равны:

;

.

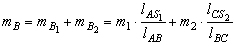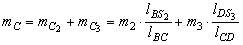Так как заменяющие массы 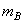и 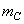совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массам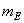и и 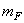, определяемыми из условий (рис. 6.4, б):

; ,

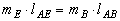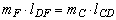где, задавая длины противовесов, можно получить их массы и наоборот.

Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса 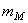(рис. 6.5), соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой скоростью 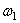, а равное ему колесо “b” вращается с той же угловой скоростью 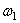, но угловые координаты противовесов отличаются на 180⁰, поэтому момент пары сил инерции от противовесов 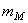равен 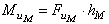. Подбирая положение точки E, можно обеспечить направление 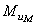, противоположное направлению 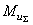, а массу противовесов 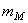определяют из условия .

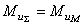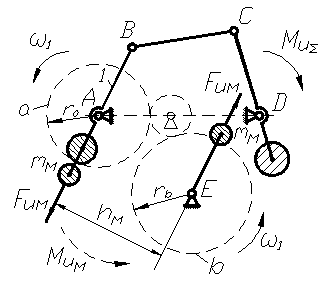
Рис.6.5

Уравновешивание роторов при проектировании

Статическое уравновешивание при проектировании

При проектировании статически уравновешивают детали, имеющие небольшие осевые размеры и конструктивно неуравновешенные, например, дисковые кулачки (рис. 6.6)

Когда кулачок неподвижен 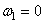, реакция в опоре 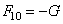.При вращении кулачка, реакция в опоре равна векторной сумме сил тяжести и центробежной силы инерции

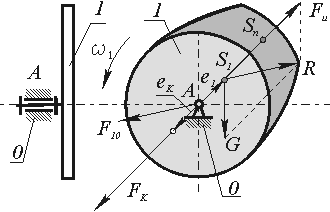
Рис.6.6

При проектировании детали типа кулачка уравновешиваются так: в деталь с центром на оси вращения вписывается окружность, подсчитываются площади ограниченные контуром кулачка и расположенные вне или внутри окружности, определяется массы и центры масс 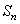неуравновешенных частей кулачка, находится эксцентриситет 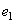центра масс 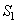кулачка по величине и направлению и определяется его дисбаланс с помощью корректирующей массы 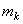, размещаемой на эксцентриситете 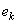, создается дисбаланс 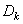равный по величине и противоположный по направлению .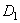