Матрицы и действия с матрицами
Введение
Настоящее пособие предназначено для знакомства с основами линейной алгебры и содержит разделы, посвященные теории матриц и теории систем линейных уравнений. Оно предназначено студентам 1-го курса и может быть полезно всем, кого интересует простое и компактное изложение материала.
В каждом параграфе содержатся основы теории, подробно разобраны примеры и приведены упражнения для самостоятельного решения. Нумерация формул и рисунков в пособии сквозная. Ключевые слова в определениях и формулировках утверждений выделены курсивом.
С развитием компьютерной техники появилась возможность решать многие задачи линейной алгебры, не очень доступные в прошлом ввиду сложности вычислений. Как известно, для решения математических задач существует много различных программных пакетов. Универсальным пакетом является пакет MATHEMATICA (см.[5]). Но даже пакет Excel (см.[6]) позволяет решить достаточно много задач линейной алгебры. Этому посвящены последние параграфы настоящего пособия. Освоив предложенные методы решения задач «вручную», рекомендуем проделать вычисления с использованием компьютера.
В качестве дополнительных учебников с подробным изложением материала рекомендуем [1,3], а в качестве задачников – [2,4].
Авторы выражают искреннюю признательность Г.М.Тащияну за неоднократные полезные обсуждения.
Матрицы и действия с матрицами
Основные понятия.
Матрицей размера 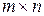 называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая 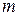 строк и
строк и 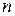 столбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойным индексом:
столбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойным индексом: 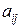 , где первый индекс
, где первый индекс 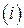 соответствует номеру строки, а второй индекс
соответствует номеру строки, а второй индекс 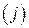 – номеру столбца. Матрица размера
– номеру столбца. Матрица размера 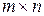 может быть записана в одном из видов:
может быть записана в одном из видов:
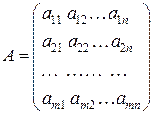
либо 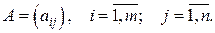
При необходимости указать размер матрицы будем использовать
запись 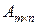 .
.
Элементы матрицы, имеющие одинаковые индексы, называются диагональными. Матрица, у которой ниже главной диагонали стоят нули, называется треугольной.
Матрица, состоящая из одной строки, называется матрицей-строкой, а матрица, состоящая из одного столбца – матрицей-столбцом. Обе такие матрицы называют также вектором.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 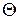 .
.
Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк (столбцов) порядком матрицы.
Квадратная матрица, у которой только диагональные элементы могут быть не равны нулю, называется диагональной матрицей.
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается 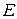 .
.
Перестановка в матрице строк со столбцами называется транспонированием матрицы. Матрица, полученная таким образом из матрицы 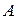 , называется к ней транспонированной и обозначается
, называется к ней транспонированной и обозначается 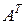 :
:
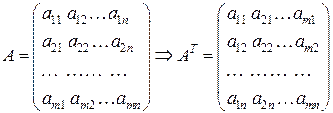 .
.
Заметим, что 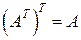 .
.
Действия с матрицами.
В математике матрица рассматривается как самостоятельный математический объект, с которым можно производить различные действия.
1. Сравнение матриц. Две матрицы равны, если они имеют одинаковый размер и соответствующие элементы равны:
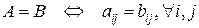 .
.
2. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо умножить на это число все элементы матрицы:
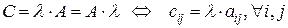 .
.
3. Сложение (вычитание) матриц. Сложение (вычитание) матриц проводится поэлементно и возможно для матриц одного размера:
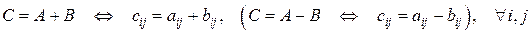 .
.
Для перечисленных выше действий справедливы следующие свойства:
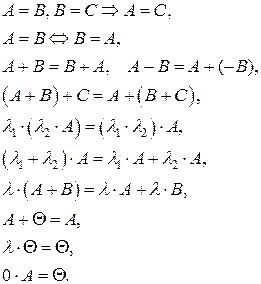
5. Умножение матриц. Матрицы перемножаются по правилу «строка на столбец»:
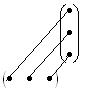
Рис.1
А именно, осуществляется операция, которая называется сумма произведений: элементы, соединенные одной линией перемножаются, а затем результаты умножения складываются. То есть, чтобы получить элемент 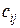 матрицы
матрицы 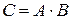 надо каждый элемент
надо каждый элемент 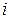 −ой строки матрицы
−ой строки матрицы 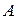 умножить на соответствующий по порядку элемент
умножить на соответствующий по порядку элемент 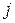 −го столбца и результаты сложить. При записи знак умножения
−го столбца и результаты сложить. При записи знак умножения 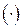 может быть опущен:
может быть опущен: 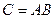 .
.
Умножение матриц возможно только в случае, если число столбцов первой матрицы равно числу строк второй матрицы. Результат умножения – матрица, имеющая число строк, совпадающее с числом строк первой матрицы, и число столбцов равное числу столбцов второй матрицы. При умножении матрицы на вектор-столбец получаем вектор-столбец. При умножении матрицы на транспонированную к ней получаем квадратную матрицу.
Умножение матриц не коммутативно.Более того, при перестановке (коммутации) матриц подчас умножение не возможно. Те квадратные матрицы, для которых выполнено свойство 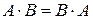 , называются коммутативными.
, называются коммутативными.
Роль единицы при умножении матриц играет единичная матрица 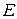 . Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:
. Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:
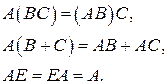
Отметим также свойство умножения и сложения для транспонированных матриц
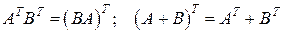 .
.
6. Возведение в степень. Для квадратных матриц возможно возведение в натуральную степень, которое проводится как последовательное умножение. При этом очевидно, справедлив коммутативный закон умножения
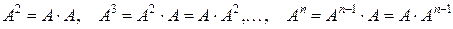 .
.
►Пример 1.
а) Даны матрицы:
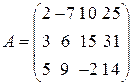 ,
, 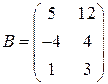 ,
, 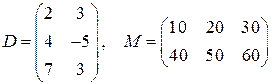 .
.
Выполнить указанные действия:
1) указать размер матрицы 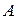 ,
,
2) записать элемент матрицы 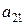 ,
,
3) найти: а) транспонированную матрицу 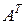 , б) матрицу
, б) матрицу 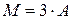 ,
,
4) вычислить 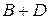 ,
,
5) вычислить 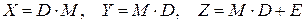 , (
, ( 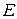 - единичная матрица).
- единичная матрица).
Решение.
1) Матрица 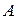 имеет 3 строки и 4 столбца, следовательно, ее размер
имеет 3 строки и 4 столбца, следовательно, ее размер 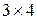 .
.
2) Элемент 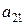 находится во второй строке и первом столбце матрицы
находится во второй строке и первом столбце матрицы 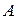 :
: 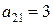 .
.
3) Транспонированная матрица получается из исходной при замене строк на столбцы, а для записи матрицы 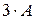 необходимо все элементы матрицы
необходимо все элементы матрицы 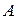 умножить на три:
умножить на три:
а) 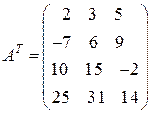 , б)
, б) 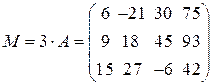 .
.
4) Матрицы 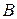 и
и 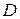 имеют одинаковый размер, следовательно, их можно складывать
имеют одинаковый размер, следовательно, их можно складывать
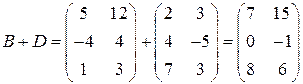 .
.
5) Число столбцов матрицы 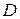 равно числу строк матрицы
равно числу строк матрицы 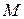 . Следовательно, возможно умножение
. Следовательно, возможно умножение 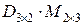 , При этом получаем матрицу
, При этом получаем матрицу 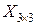 , имеющую три строки и три столбца:
, имеющую три строки и три столбца:
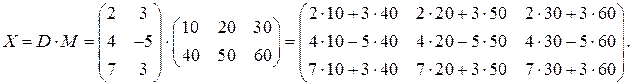
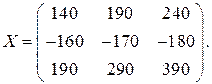
Аналогично возможно и умножение 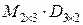 , получаем матрицу
, получаем матрицу 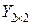 .
.
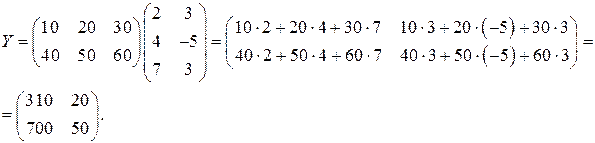
Так как складывать можно только матрицы одного размера, для нахождения матрицы 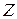 необходимо взять единичную матрицу второго порядка:
необходимо взять единичную матрицу второго порядка:
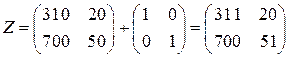 . ◄
. ◄
Упражнения.
1. Даны матрицы: 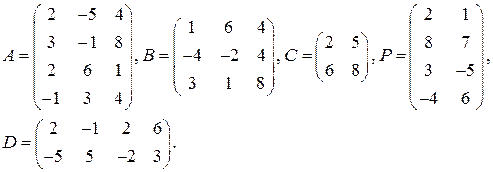
Выполнить действия:
а) 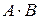 , б)
, б) 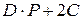 , в)
, в) 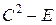 , г)
, г) 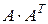 , д)
, д) 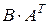 .
.
Ответы:
а) 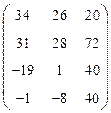 , б)
, б) 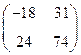 , в)
, в) 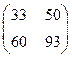 , г)
, г) 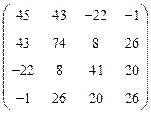 ,
,
д) 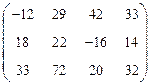 .
.
Определители и их свойства
Определителем (детерминантом) n-го порядка называется числовая характеристика квадратной матрицы A размера 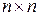 , вычисляемая по определенному правилу (см., например,
, вычисляемая по определенному правилу (см., например, 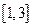 ). Обозначается определитель одним из следующих символов:
). Обозначается определитель одним из следующих символов: 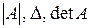 .
.
Определитель первого порядка – определитель для матрицы размера 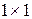 , состоящей из одного числа, – равен самому числу:
, состоящей из одного числа, – равен самому числу:
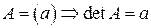 .
.
Для определителей второго и третьего порядков имеем:
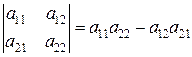 ; (1)
; (1)
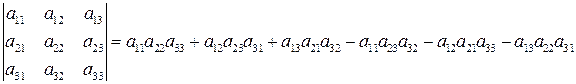 (2)
(2)
При вычислении определителя третьего порядка удобно пользоваться следующей схемой (схема Саррюса):
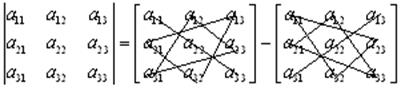
Рис. 2
Определитель равен алгебраической сумме произведений элементов, соединенных на рисунке одной непрерывной линией. Для определителей порядка выше третьего подобных простых схем не составлено, и для вычисления надо использовать упрощения, основанные на свойствах определителей.
Введем несколько важных понятий.
Минором 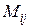 определителя
определителя 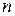 −го порядка называется определитель, полученный из данного вычеркиванием
−го порядка называется определитель, полученный из данного вычеркиванием 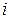 −ой строки и
−ой строки и 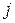 −го столбца.
−го столбца.
В общем случае минором прямоугольной матрицы называется любой определитель, полученный из нее в результате вычеркивания каких-то строк или столбцов.  В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры
В частности, сам определитель квадратной матрицы тоже является ее минором. Миноры 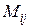 выделены в силу их важности для приложений.
выделены в силу их важности для приложений.
Алгебраическим дополнением к элементу 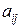 определителя
определителя 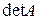 называется выражение
называется выражение
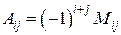 .
.
Для вычисления определителя 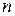 −го порядка справедливы рекуррентные формулы через определители (
−го порядка справедливы рекуррентные формулы через определители ( 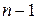 )−го порядка:
)−го порядка:
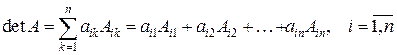 (3)
(3)
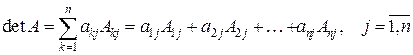 . (4)
. (4)
Формулы представляют разложение определителя: (3) − по элементам строки, (4) − по элементам столбца, и, в частности, показывают, что определитель не изменяется при перестановке строк со столбцами, т.е. определители исходной матрицы и транспонированной к ней равны.
Свойства определителей
Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов.
1. Определитель, имеющий нулевую строку равен нулю.
2. Определитель, у которого две строки равны или пропорциональны, равен нулю.
3. Общий множитель строки можно выносить за знак определителя.
4. Перестановка двух строк определителя изменяет знак определителя.
5. Если строку определителя умножить на постоянное число и прибавить к другой строке, то определитель не изменится.
6. Сумма произведений элементов строки на соответствующие алгебраические дополнения к элементам другой строки равна нулю.
7. Определитель можно представить в виде суммы определителей согласно формуле
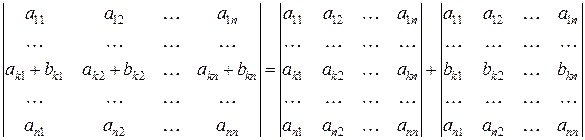 .
.
8. Определитель 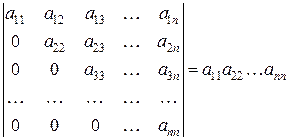 .
.
То есть определитель треугольной матрицы равен произведению ее диагональных элементов.
9. Определитель произведения квадратных матриц равен произведению определителей этих матриц: 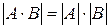 .
.
►Пример 2. Вычислить определители:
1)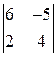 ,2)
,2)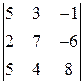 ,3)
,3) 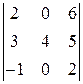 , 4)
, 4) 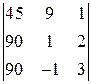 , 5)
, 5) 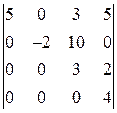 ,
,
6) 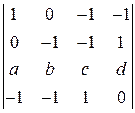 , 7)
, 7) 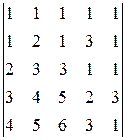 .
.
Решение.
1) Определитель вычислим по формуле (1)
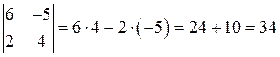 .
.
2) Сравним вычисления по формуле (2) и по формуле (3). По формуле(2) 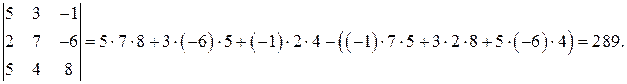 Для вычисления по формуле (3) возьмем вторую строку (выбор строки произволен) и вычислим миноры и алгебраические дополнения к элементам этой строки
Для вычисления по формуле (3) возьмем вторую строку (выбор строки произволен) и вычислим миноры и алгебраические дополнения к элементам этой строки
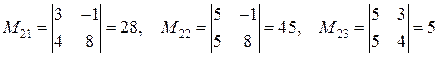 .
.
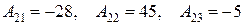 .
.
По формуле (3) имеем 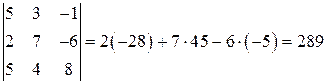 .
.
3) В определителе 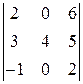 во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
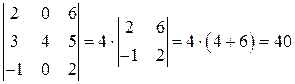 .
.
4) Первый столбец определителя 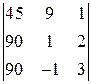 имеет общий множитель. Вынесем этот множитель за знак определителя
имеет общий множитель. Вынесем этот множитель за знак определителя
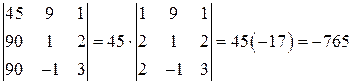 .
.
5) Имеем определитель треугольной матрицы 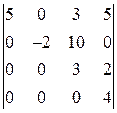 , следовательно, по свойству (8)
, следовательно, по свойству (8)
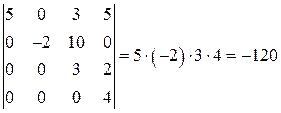 .
.
6) Воспользуемся формулой (3), а определители третьего порядка вычислим по схеме Саррюса:
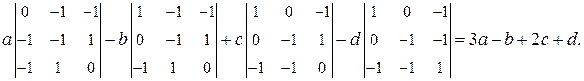 ◄7) Определитель
◄7) Определитель 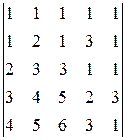 имеет пятый порядок. Разложение по элементам строки (столбца) приводит к пяти определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем:
имеет пятый порядок. Разложение по элементам строки (столбца) приводит к пяти определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем:
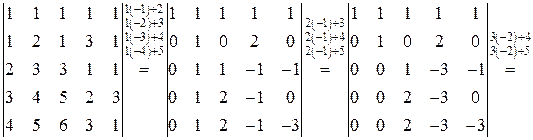
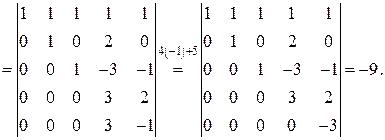 ◄
◄
►Пример 3. Решить уравнение 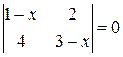 .
.
Решение. По формуле (1) раскроем определитель, а затем решим уравнение
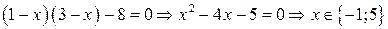 . ◄
. ◄
Упражнения.
1. Вычислить определители:
а) 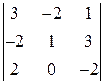 ; б)
; б) 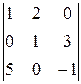 ; в)
; в) 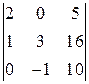 ; г)
; г) 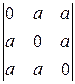 ;
;
д) 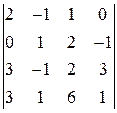 ; е)
; е) 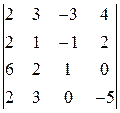 ; ж)
; ж) 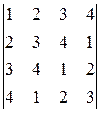 ;
;
з) 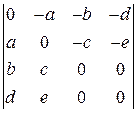 ; и)
; и) 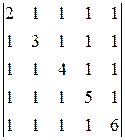 ; к)
; к) 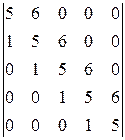 .
.
Ответы:
а) -12; б) 29; в) 87; г) 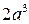 ; д) 0; е) 48; ж) 160; з)
; д) 0; е) 48; ж) 160; з) 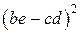 ;и) 394; к) 665.
;и) 394; к) 665.
Упражнения.
1. Для заданных матриц найти обратную матрицу:
а) 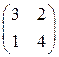 ; б)
; б) 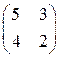 ;в)
;в) 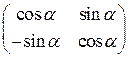 ;г)
;г) 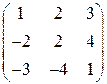 ;д)
;д) 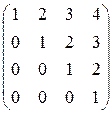 .
.
Ответы:
а) 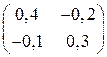 ; б)
; б) 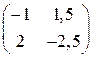 ;в)
;в) 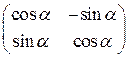 ;
;
г) 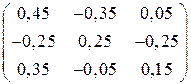 ; д)
; д) 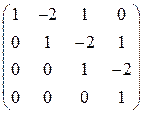 .
.
2. Найти неизвестную матрицу 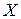 из уравнений:
из уравнений:
а) 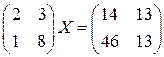 ; б)
; б) 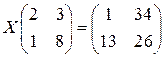 ;
;
Ответы: а) 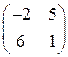 ; б)
; б) 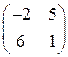 ;
;
Ранг матрицы
Рангом матрицы 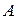 (обозначение:
(обозначение: 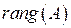 или
или 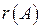 ) называется порядокотличного от нуля минора этой матрицы при условии, что все ее миноры более высоких порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто базисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
) называется порядокотличного от нуля минора этой матрицы при условии, что все ее миноры более высоких порядков равны нулю. Минор наивысшего порядка, отличный от нуля, называется базисным минором или просто базисом. Матрица может иметь несколько различных базисов. Для определения базиса над матрицей производят элементарные преобразования, при которых ранг матрицы не изменяется.
К элементарным преобразованиям матрицы относятся:
- транспонирование;
- удаление или добавление строки (столбца), состоящей из нулей;
- умножение строки (столбца) на число, отличное от нуля;
- перестановка строк (столбцов);
-прибавление к элементам какой-либо строки элементов другой строки, умноженных на постоянное число (то же самое для столбцов).
Выполняя элементарные преобразования над матрицей, получаем другую матрицу, называемую эквивалентной. Используя выше перечисленные действия, матрицу можно преобразовать к эквивалентной, имеющей треугольный вид, что позволяет легко определить ее ранг.
►Пример 5. Найти ранг матрицы 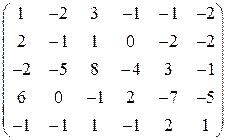 .
.
Решение. Переход от исходной матрицы к эквивалентной будем обозначать символом “ 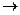 ”, над котором указаны действия, проводимые со строками (см.пример 2). Преобразуем матрицу:
”, над котором указаны действия, проводимые со строками (см.пример 2). Преобразуем матрицу:
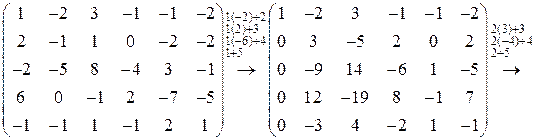
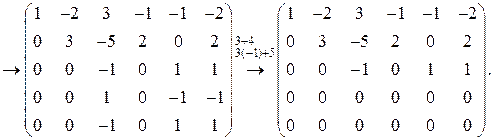
Минор 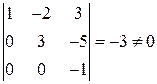 , а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно,
, а все миноры четвертого порядка равны нулю, т.к. содержат нулевую строку. Следовательно, 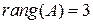 . ◄
. ◄
При преобразовании матрицы мы действовали по определенному алгоритму. Этот метод стандартный, он называется методом Гаусса.
Упражнения.
1. Найти ранг матриц:
а) 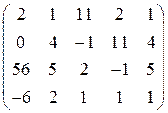 ; б)
; б) 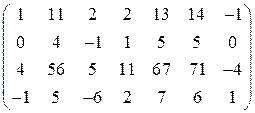 ;
;
в)  ; г)
; г) 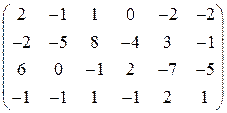 .
.
Ответы: а) 4; б) 2; в) 4; г) 3.
Системы линейных уравнений
Основные понятия.
Системой 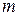 линейных уравнений с
линейных уравнений с 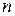 неизвестными
неизвестными 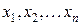 (линейной системой) называется система вида
(линейной системой) называется система вида
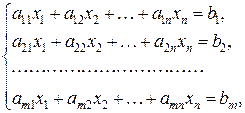 (7)
(7)
где 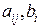 − заданные числа. Числа
− заданные числа. Числа 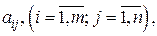 называются коэффициентами системы, а числа
называются коэффициентами системы, а числа 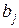 - свободными членами.
- свободными членами.
Линейная система называется однородной, если все свободные члены равны нулю, т.е.
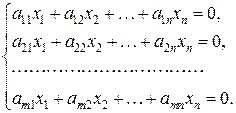 (8)
(8)
В противном случае линейная система называется неоднородной.
Решением системы (7) называется упорядоченная совокупность 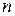 чисел:
чисел:
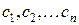 , (9)
, (9)
при подстановке которых вместо 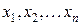 каждое уравнение системы обращается в тождество.
каждое уравнение системы обращается в тождество.
Система, имеющая хотя бы одно решение, называется совместной, а система, не имеющая ни одного решения, - несовместной. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Однородная система (8) всегда совместна, так как она имеет очевидное решение: 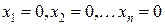 . Нулевое решение однородной системы называется тривиальным.
. Нулевое решение однородной системы называется тривиальным.
Две системы называются равносильными или эквивалентными, если любое решение одной из них является также решением и другой, и обратно, т.е. они имеют одно и то же множество решений. В частности, любые две несовместные системы являются эквивалентными.
Линейную систему можно записать в матричной форме. Введем матрицы:
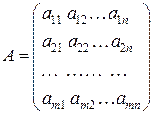 – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных,
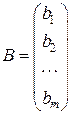 – матрица-столбец свободных членов,
– матрица-столбец свободных членов,
 – матрица-столбец неизвестных.
– матрица-столбец неизвестных.
Тогда систему (7) можно записать в виде матричного уравнения 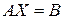 , а решение (9) в виде матрицы-столбца
, а решение (9) в виде матрицы-столбца 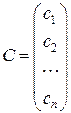 . Иногда для экономии места в ответах упражнений будем его записывать в виде матрицы-строки.
. Иногда для экономии места в ответах упражнений будем его записывать в виде матрицы-строки.
Матрица коэффициентов 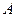 называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов
называется основной матрицей системы. Матрица, составленная из коэффициентов и свободных членов 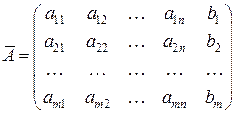
называется расширенной матрицей системы.
Выражение «решить систему» означает, что надо выяснить, совместна ли система, а в случае совместности – найти все ее решения
Теорема Крамера.
Пусть дана система, в которой число уравнений совпадает с числом неизвестных
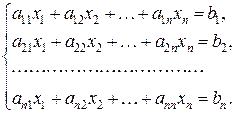 (10)
(10)
Если определитель основной матрицы системы
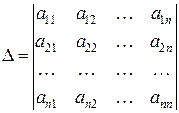 , (11)
, (11)
не равен нулю, то система имеет единственное решение 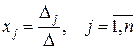 , где
, где
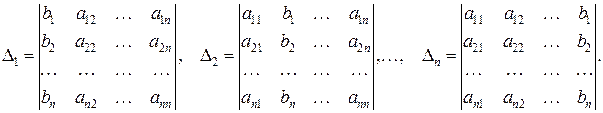
Определители 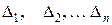 , получены из определителя
, получены из определителя 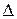 заменой соответствующего столбца на столбец свободных членов.
заменой соответствующего столбца на столбец свободных членов.
►Пример 6.По формулам Крамера найти решение системы уравнений 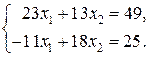
Решение. Вычислим определители и найдем решение:
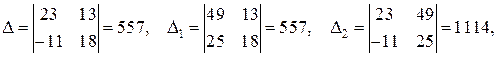
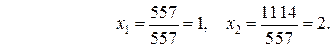 Ответ:
Ответ: 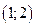 .◄
.◄
Упражнения.
Решить системы по формулам Крамера:
1) 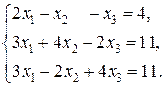 2)
2) 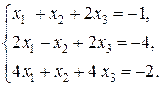 3)
3) 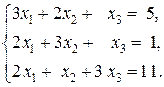
Ответы: 1) 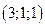 , 2)
, 2) 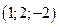 , 3)
, 3) 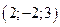 .
.
Упражнения.
Найти решение систем с помощью обратной матрицы:
а) 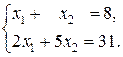 б)
б) 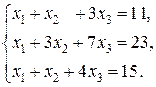 в)
в) 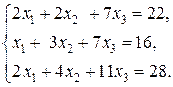
г) 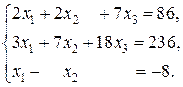
Ответы: а) 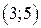 ; б)
; б) 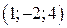 ; в)
; в) 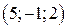 г)
г) 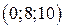 .
.
Теорема Кронекера-Капелли.
Для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг ее основной матрицы ( 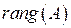 ) был равен рангу расширенной матрицы (
) был равен рангу расширенной матрицы ( 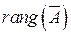 ).
).
Пусть 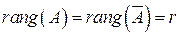 . Тогда верны следующие утверждения.
. Тогда верны следующие утверждения.
1.Если ранг матрицы 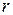 равен числу неизвестных
равен числу неизвестных 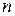 , то система имеет единственное решение.
, то система имеет единственное решение.
2. Если ранг матрицы 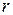 меньше числа неизвестных, то система имеет бесконечное множество решений. При этом
меньше числа неизвестных, то система имеет бесконечное множество решений. При этом 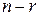 неизвестных, которые называются свободными неизвестными, принимают произвольные значения. Говорят, что система имеет
неизвестных, которые называются свободными неизвестными, принимают произвольные значения. Говорят, что система имеет 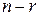 степеней свободы.
степеней свободы.
Метод Гаусса (исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы. Она аналогична процедуре, используемой для отыскания ранга матрицы.
Составим расширенную матрицу системы и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.
Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.
Рассмотрим примеры на три ситуации, возникающие при исследовании линейных систем.
1)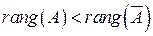 .Система несовместна.
.Система несовместна.
►Пример 8.
Решить систему уравнений методом Гаусса:
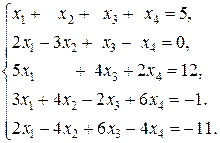
Решение. Составим расширенную матрицу и преобразуем ее:
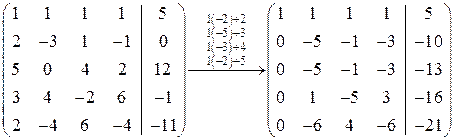 .
.
Как и в примере 2 над стрелкой указаны выполняемые операции.
Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки - в третьем столбце:
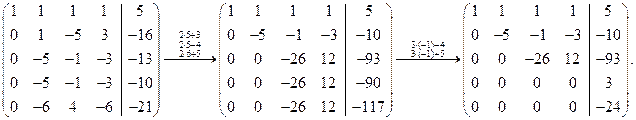 В четвертой, пятой строках легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой и пятой.
В четвертой, пятой строках легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой и пятой.
По преобразованной матрице определяем: 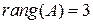 ,
, 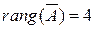 ,
,
следовательно, данная система уравнений несовместна.
Ответ: система не имеет решений. ◄
2)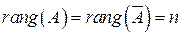 .Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.
.Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.
►Пример 9.Решить систему уравнений методом Гаусса
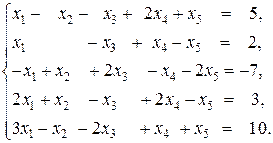
Решение. Составим расширенную матрицу и преобразуем ее (последнее действие – перестановка 4-й и 5-й строк):
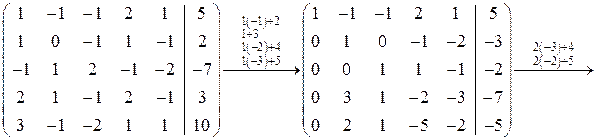
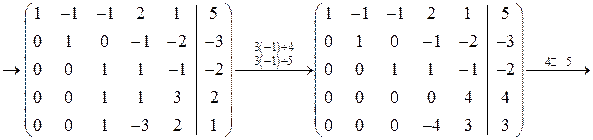
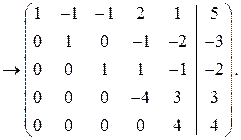
Ранг основной матрицы равен рангу расширенной матрицы 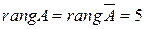 и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной
и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной
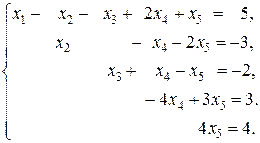
Полученная система имеет ступенчатый вид и легко решается.
Ответ: 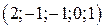 .◄
.◄
3)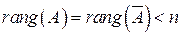 .Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося слагаемые со свободными неизвестными в правую часть уравнений.
.Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося слагаемые со свободными неизвестными в правую часть уравнений.
►Пример 10.Решить систему уравнений
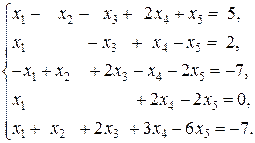
Решение. Преобразуем расширенную матрицу системы
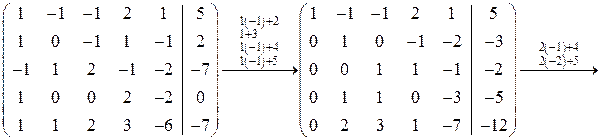
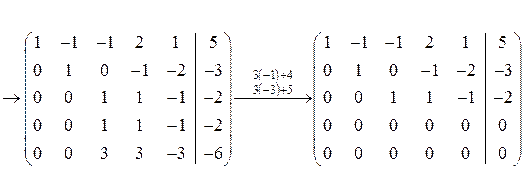 .
.
Ранг основной матрицы равен рангу расширенной матрицы 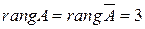 , число неизвестных равно пяти. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестными
, число неизвестных равно пяти. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестными 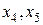 и выразим через них
и выразим через них 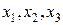 :
:
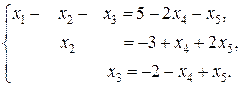 отсюда получаем
отсюда получаем 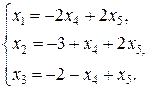
Ответ запишем в виде вектора-столбца. 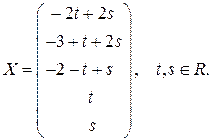 ◄
◄
Выбор свободных неизвестных можно делать по-разному. Однако не всякие 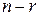 неизвестных можно принять свободными. Необходимо, чтобы коэффициенты при остальных
неизвестных можно принять свободными. Необходимо, чтобы коэффициенты при остальных 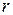 неизвестных составили базисный минор. Так, если за базисный минор принять минор
неизвестных составили базисный минор. Так, если за базисный минор принять минор 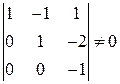 , то свободными неизвестными будут
, то свободными неизвестными будут 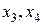 , и решение принимает вид
, и решение принимает вид 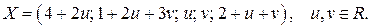 Рекомендуем студентам получить это решение самостоятельно и сделать проверку.
Рекомендуем студентам получить это решение самостоятельно и сделать проверку.
Упражнения.
Исследовать и решить системы уравнений:
1) 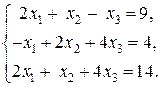 Ответ:
Ответ: 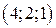 .
.
2) 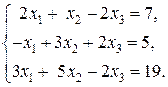 Ответ:
Ответ: 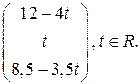
3) 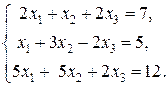 Ответ:
Ответ: 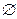 .
.
4) 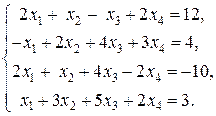 Ответ:
Ответ: 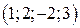 .
.
5) 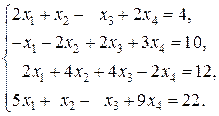 Ответ:
Ответ: 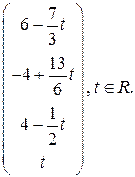
6) 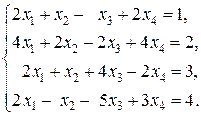 Ответ:
Ответ: 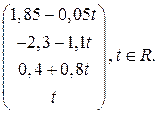 .
.
7) 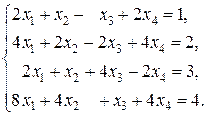 Ответ:
Ответ: 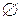 .
.
Однородные системы.
Система однородных уравнений всегда совместна. Если ранг матрицы коэффициентов равен числу неизвестных, то система имеет единственное нулевое (тривиальное) решение.
Если ранг матрицы 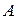 однородной системы на единицуменьше числа неизвестных, то система имеет одну степень свободы, и ее решение можно записать через миноры матрицы
однородной системы на единицуменьше числа неизвестных, то система имеет одну степень свободы, и ее решение можно записать через миноры матрицы 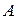 . Для этого в матрице
. Для этого в матрице 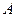 необходимо оставить
необходимо оставить 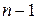 линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
линейно независимых строк, а затем вычислить миноры, поочередно вычеркивая столбцы и изменяя знак при каждом переходе.
Так для системы двух линейных однородных уравнений с тремя неизвестными
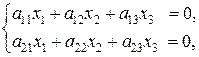 (12)
(12)
решение имеет вид:
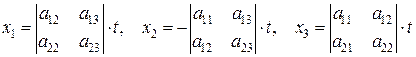 , где
, где 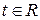 , если хотя бы один из определителей второго порядка не равен нулю.
, если хотя бы один из определителей второго порядка не равен нулю.
►Пример 11.Решить систему
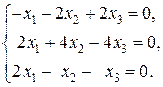
Решение.
Матрица коэффициентов 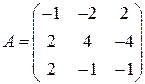 ;
; 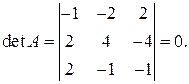
Минор 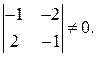 Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Второе уравнение в системе пропорционально первому, и его можно убрать и получить систему вида (12). Матрице
Следовательно, ранг матрицы коэффициентов равен двум и на единицу меньше числа неизвестных. Второе уравнение в системе пропорционально первому, и его можно убрать и получить систему вида (12). Матрице 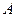 эквивалентна матрица
эквивалентна матрица 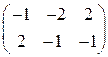 , имеющая две линейно независимых строки. Тогда решение получаем в виде:
, имеющая две линейно независимых строки. Тогда решение получаем в виде:
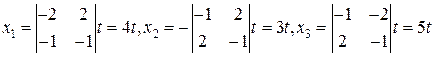 .
.
Ответ можно записать в виде вектора 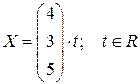 .◄
.◄
Упражнения.
Решить системы:
1) 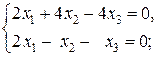 2)
2) 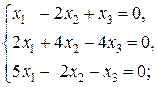 3)
3) 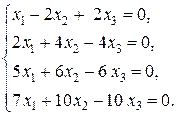
Ответы: 1) 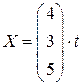 ; 2)
; 2) 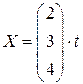 ; 3)
; 3) 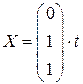 ;
; 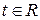 .
.
Упражнения.
Найти собственные числа, и для действительных собственных чисел найти собственные векторы матриц:
1) 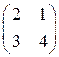 , 2)
, 2) 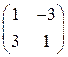 , 3)
, 3) 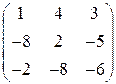 , 4)
, 4) 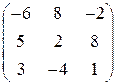 , 5)
, 5) 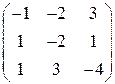 , 6)
, 6) 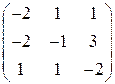 , 7)
, 7) 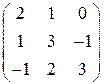 .
.
Ответы:
1) 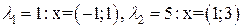 ;
;
2) 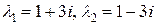 ;
;
3) 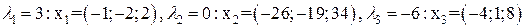 ;
;
4) 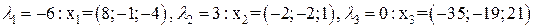 ;
;
5)
