Необходимое условие локального экстремума

Если функция u=f(x1,x2…xn) имеет в точке Mo( 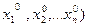частные производные первого порядка по всем переменным Х1,Х2,Х3…Хn и имеет в т Мо локальный экстремум, то все частные проиводные первого порядка в точке Мо обращаются в 0.

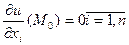
Все точки в который частные производные обращаются в 0, в которых все необъодимые условия экстремума выполнены, называются стационарными точками.

Замечание: необходимое условие экстремума может быть записано так: Если функция u=f(m) дифференцируема в точке Мо и имеет в этой точке локальный экстремум, то дифференциал функции du(Mo)=0(тождественное равенство), т.е.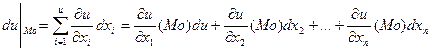

Достаточные условия локального экстремума функции N переменных.

Пусть функция u=f(M) один раз дифференцируема в некоторой окрестности точки Мо и два раза дифференцируема в самой точке Мо, пусть кроме того Мо – стационарная точка. Тогда:

1. Если d²u в точке Мо положительно определенная квадратичная форма относительно переменных dx1,dx2,…,dxn, то Мо – точка локального минимума

2. Если d²u в точке Мо отрицательно определенная квадратичная форма, то Мо – точка локального Максимума.

3. Если d²u в точке Мо знакопеременная квадратичная форма, то экстремум в точке Мо не существует.

Частный случай:

[Т] пусть функция u=f(x,y) один раз дифференцируема в окрестности точки Мо с координатами (хо,уо) и два раза дифференцируема в самой точке Мо и пусть Мо – стационарная точка, тогда если в точке Мо выполнено условие:

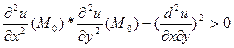, то функция имеет в точке Мо локальный экстремум, причем если 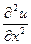в точке Мо>0 , то Мо точка локального минимума.

Если 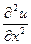(Мо)<0 то Мо точка локального Max

Если же 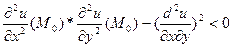то экстремум в точке Мо не существует.

Неявные функции.

Def Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.

Частные производные неявно заданной функции вычисляются по формулам:

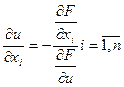
Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:

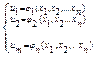(1)

Пусть функции определены, как решение М функциональных уравнений 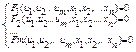(2)

(2)

Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.

Def Это решение будем называть непрерывным и дифференцируемом в некоторой области D изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.

=

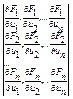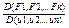
Такой определитель называют определителем Якоби или Якобианом.

[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, 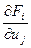непрерывна в точке Мо, Якобиан 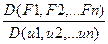отличен от 0 и F1=F2=…=Fn в точке Мо

Условный экстремум

Задача отыскания экстремума функции аргументы которой удовлетворяют дополнительному условию связи называется задачей отыскания условного экстремума.

Рассмотрим вопрос отыскания экстремума функции z=f(u1,u2,…um,x1,x2,…,xn)

Будем говорить, что эта функция при наличии условий связи 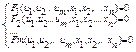(2) имеет условный максимум (минимум) в точке Мо, координаты которой удовлетворяют этим условиям связи, если существует окрестность точки Мо, для которой значение этой функции в точке Мо является наибольшим (наименьшим) среди всех точек координаты которых удовлетворяют эти условиям связи.

Первый способ решения задачи условного экстремума:

Основная его идея – переход от задачи условного экстремума к задаче безусловного экстремума.

Пусть у функции F1, F2, …Fm дифференцируема в окрестности точки Mо и 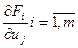непрерывны в окрестности точки Мо. Пусть, кроме того, Якобиан 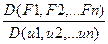неравен 0 в точке Мо. Тогда система (2) имеет непрерывное дифференцируемое решение 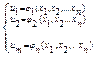. Подставим это решение в функцию 2: z=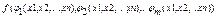

Метод множителей Лагранжа.

Метод неопределенных множителей Лагранжа. Если система функций уравнений (2) неразрешима, либо ее решение затруднительно для вас, используют более универсальный способ – метод неопределенных множителей Лагранжа. Идея та же – переход от условного экстремума к безусловному.

L=f+l1F1+l2F2+…+lmFm (4)

Функция Лагранжа.

Теперь находим экстремум этой функции. Здесь l1, l2,…ln –множители Лагранжа.

Предположим, что функция дифференцируема

L(u1,u2,…um,x1,x2,…,xn,l1,l2,…ln)

Необходимые условия экстремума:

Эта система содержит u+2m уравнений и u+2m переменных.

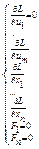
Мо(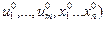

lо(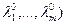

Для полученных точек проверяем достаточное условие экстремума.