Решение системы нелинейных уравнений
Функция Find(z1, z2, . . .) – возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блоком решения уравнений.
Пример решения системы нелинейных уравнений приведен ниже на рисунке 13.
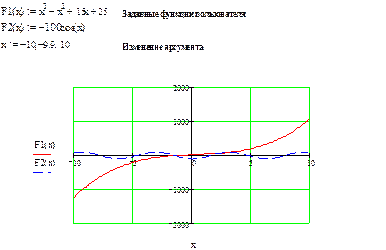
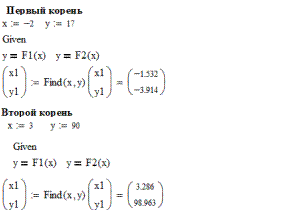
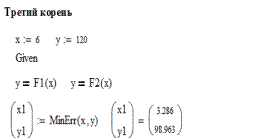
Рис. 13Пример решения системы нелинейных уравнений
Вывод из решения данной системы уравнений следующий: уравнение имеет два корня и результат решения с помощью функции MinErr подтверждает это. Функция MinErr приводит к минимальной ошибке.
Для решения систем линейных уравнений также можно использовать функцию Find. Пример подобного применения представлен на рис. 9.
Контрольные вопросы
1. Назовите способы решения систем линейных уравнений.
2. Формат функции lsolve()
3. С помощью, каких функций можно решить систему нелинейных уравнений?
4. В каких случаях при решении систем нелинейных уравнений используется функция Find()?
5. В каких случаях при решении систем нелинейных уравнений используется функция Minerr()?
6. Какие функции выполняет директива Given?
7. Какие функции используются с директивой Given?
8. Какая функция приводит к минимальной ошибке?
9. Назовите ограничения, при использовании блока Given.
Лабораторная работа №5
Решение уравнений с помощью программного модуля
Подготовка к работе
По указанной литературе изучить:
- задание функций пользователя;
- операторы присваивания;
- состав палитры Programming Palette (Программирование);
- программирование вложенных условных выражений;
- возможности системы программирования для организации циклов с известным числом повторений с помощью оператора for…;
- возможности системы программирования для организации циклов с неизвестным числом повторений с помощью операторов while…;
Задание и порядок выполнения работы.
1. Рассчитать значения заданной функции с использованием программного блока. Предусмотреть ввод данных с использованием оператора как локального, так и глобального присваивания. Задание в таблице 8. Построить график заданной функции с шагом 0,3.
2. Используя оператор условных выражений, вычислить функцию, выбранную из табл. 2 согласно варианту. Протестировать все ветви разветвляющегося процесса: вывести несколько значений заданной функции из разных диапазонов области (xo ¸ xn) определения функции. Построить график заданной функции с шагом 0,1.
3. Используя оператор цикла for, вычислить сумму или произведение (в зависимости от номера варианта) конечного ряда, заданного в табл.9. Вывести значение заданной функции. Проверить полученный результат с помощью калькулятора.
4. Вычислить функцию fact=(k+N)! для произвольного целого k, где N – номер варианта (цифра от 1 до 12). Вывести несколько значений заданной функции. Проверить полученный результат с помощью калькулятора.
Таблица 8
Варианты заданий
| № | Функция | № | Функции |
| 1. | y=x2(x+1) – b*sin(x+1) x=[-2.5 … 2] b=3 | 9. | z=x3 + b*sin(x) – a2 x=[-5 .. 5 a=5 b= -2] |
| 2. | 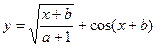 x=[-3.5 … 3] b=2; a = 3 x=[-3.5 … 3] b=2; a = 3 | 10. | 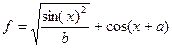 x=[-4 .. 4] b=3 a = 2 x=[-4 .. 4] b=3 a = 2 |
| 3. | z = ln(x)2 +b-x x=[-2 .. 2] b=10 | 11. | y=ln(x) + sin(a+x)/b x=[-3 .. 3] b=2 a=1.5 |
Продолжение таблицы 8
| 4. | w= sin(x)3 +b*x2 – 10a x=[-3 .. 3] b=3; a=1.5 | 12. | f= cos(x+b) – a2 x=[-2.5 … 2] b=2 a=3 |
| 5. | 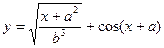 x=[-3.5 .. 3.5] a=2; b=5 x=[-3.5 .. 3.5] a=2; b=5 | 13. | 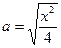 +sin(x+b)2 x=[-4 .. 4] b=3 +sin(x+b)2 x=[-4 .. 4] b=3  |
| 6. | z = e-bx (x+a2)/b x=[-2 .. 2.5] a=2.5 b=4 | 14. | s= (x – b)2/2 – sin(x)2 x=[-3.5 3] b=2 |
| 7. | w = (a – x)* (b – a)/x2+b x=[-4 .. 4] b=1.5 a=2 | 15. | y= (x+b)3/2x2 + cos(x) x=[-2.5…3] b=3 |
| 8. | 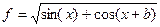 x=[-3 .. 3] b=3 x=[-3 .. 3] b=3 |
Таблица 9
Варианты заданий
| № | Функция | № | Функция |
| 1. | 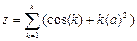 a=3 a=3 | 9. | 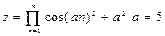 |
| 2. | 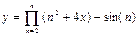 x=2 x=2 | 10. | 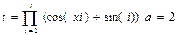 |
| 3. | 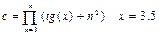 | 11. | 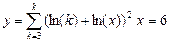 |
| 4. | 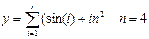 | 12. | 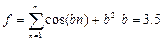 |
| 5. | 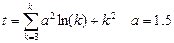 | 13. | 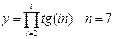 |
| 6. | 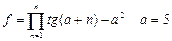 | 14. | 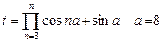 |
| 7. | 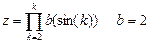 | 15. | 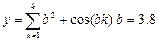 |
| 8. | 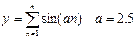 |
Методические указания
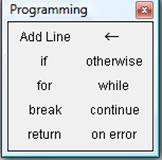 Набор программных элементов для создания программных модулей весьма ограничен и содержит следующие элементы: Add Line, ←, if, otherwise, for, while, break, continue, return, on error.
Набор программных элементов для создания программных модулей весьма ограничен и содержит следующие элементы: Add Line, ←, if, otherwise, for, while, break, continue, return, on error.
Оператор добавления линии Add Line выполняет функции расширения программного блока. Расширение фиксируется удлинением вертикальной черты. Благодаря этому можно создавать сколь угодно большие программы.
Оператор внутреннего присвоения ← выполняет функцию внутреннего локального присвоения. Локальный характер присвоения означает, что такое значение переменной сохраняется только в теле программы. За пределами тела программы значение переменной может быть неопределенным, либо равно значению, которое задается вне программного блока операторами локального := или глобального  присвоения.
присвоения.
Глобальным оператором переменная может быть определена в любом месте документа.
