Симплексный метод решения задач линейного программирования средствами Mathcad
Данный метод является методом целенаправленного перебора опорных решений задачи линейного программирования. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что оптимальное решение отсутствует.
Решить симплексным методом задачу:

Решение:
Приводим задачу к каноническому виду.
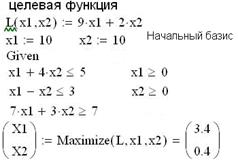
Значение целевой функции при этом базисе равно: 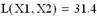
При поиске минимума используется функция Minimize/
Краткие итоги по теоретической части
Основная идея системы Mathcad – предоставление пользователю возможности описывать на экране вычисления в форме, очень близкой к общепринятой математической нотации, применяемой при записи математических моделей и алгоритмов численного анализа.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Лабораторные работы направлены на получение навыков использования математических пакетов в решении различных математических и инженерных задачах, в представлении полученных результатов различными методами (табличном, графическом виде).
Все работы выполняются по вариантам, задаваемым преподавателем. После выполнения работы оформляется отчет.
Цель практической части:Научить студентов работе в системе Mathcad. Получить навыки решения уравнений разной сложности, использовать математические и статистические функции всистеме Mathcad.
Содержание отчета
- Название работы.
- Результаты выполнения заданий.
- Выводы по работе относительно используемых операторов, функций и полученных результатов.
Лабораторная работа №1
Табулирование функций и нахождение корней уравнений
в системе Mathcad
Подготовка к работе
По указанной литературе изучить:
- правила ввода текста, данных, переменных;
- задание функций пользователя;
- операторы присваивания;
- правила построения графиков и графические средства для работы с ними;
- правила вывода таблиц с результатами вычислений;
- состав и назначение элементов Math Palette (палитры математических символов).
Задание и порядок выполнения работы
- Создать в текстовой области заголовок документа "Вычисления в Mathcad".
- Задать выражение для расчета заданной переменной, выбранную из табл. 1. в соответствии с вариантом, для конкретного значения аргумента.
- Задать это выражение как функцию пользователя.
- Задать ранжированную переменную, изменяющуюся в пределах xo¸xn с шагом h=0.1. Рассчитать и вывести в виде таблицы значения функции при изменении аргумента в заданном интервале.
5. Для данной функции построить XY - график. Отформатировать его для наглядного представления заданной функции.
6. Построить график функции f(x) и приблизительно определить один из корней уравнения. Решить уравнение f(x)= 0 с точностью ε = 10 - 4 с помощью встроенной функции Mathcad root. Варианты заданий (Таблица 1);
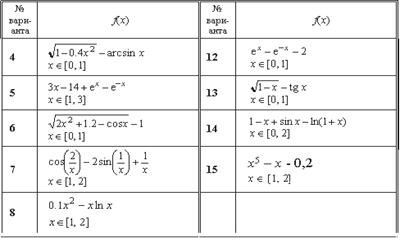
Таблица 1
Варианты заданий
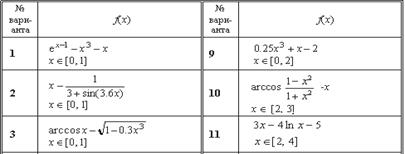
Продолжение таблицы 1
7. Найти корни полинома с помощью функции polyroots. Задать вектор V, содержащий коэффициенты полинома. Коэффициенты полинома найти с использованием символьной команды. Варианты заданий (Таблица 2)
Таблица 2
Варианты заданий
| № варианта | g(x) | № варианта | g(x) |
| x4 – 2x3+x2 – 12x+20 | x4+x3 – 17x2 – 45x – 100 | ||
| x4+6x3+x2+x2 – 4x – 60 | x4 – 5x3 +2x2 –15x+50 | ||
| x4 – 14x3 – 40x – 75 | x4 – x3 –x2 – 20x+25 | ||
| x4 – x3+x2 – 11x+10 | x4+5x3+7x2 – 5x+95 | ||
| x4 – x3+13x2 – 31x + 25 | x4 – 7x3+17x2+x – 20 | ||
| x4+7x3+9x2+13x – 30 | x4+10x3+36x2+70x+75 | ||
| x4+3x3 – 23x2 – 55x – 150 | x4+9x3+39x2+59x+60 | ||
| x4 – 6x3+4x2–10x+75 |
Методические указания
Пример выполнения задания лабораторной работы
Чтобы определить начальное приближение по хвоспользуемся графиком. По команде Format →Graph → Trace, выплывет окно, показанное на рис. 10, по нему определите приближенное значение х,предварительно нужно щелкнуть по точке пересечения графика функции с осью абсцисс.
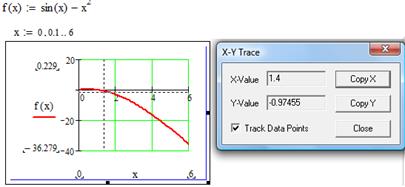
Рис. 10 Определение приближенного значения х
По графику обнаружено начальное приближение х= 1.4
Изменение системного параметра TOL (рис.11). Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL:=0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика à Параметры… à Переменныеà Допуск сходимости (TOL), (Toolsà Workscheetà Convergence Tolerance(TOL) – в англоязычном Mathcad)
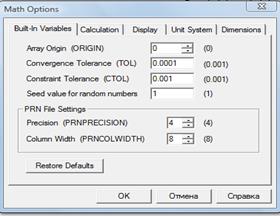
Рис. 11 Окно системных параметров
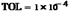 Установленозначение
Установленозначение
Контрольные вопросы
1. Поясните структуру окна системы Mathcad.
2. Какие приёмы создания текстовой области Вы знаете?
3. Перечислите приоритетность выполнения операций в выражениях.
4. Какие типы данных используются в системе Mathcad?
5. Дайте понятие идентификатора.
6. Какие требования предъявляются к идентификаторам?
7. Дайте понятие переменной.
8. Как задать переменную в системе Mathcad?
9. Что такое ранжированная переменная?
10. Для решения, каких задач используется ранжированная переменная?
11. Дать понятие функции пользователя?
12. Назовите оператор присвоения системы Mathcad?
13. Назовите оператор вывода системы Mathcad?
14. Как вывести результаты вычислений в виде таблиц?
15. Как создать и отредактировать XY - график?
Лабораторная работа №2
Функции условных выражений
Подготовка к работе
По указанной литературе изучить:
‒ категории функций;
‒ операции отношений;
‒ правила записи функции условных выражений;
‒ состав палитр Evaluation and Boolean (Отношения) .
Задание и порядок выполнения работы
1 Задать условную функцию с использованием функции if и условий. Варианты заданий в таблице 3
2 Задать эту функцию, используя операторы if и otherwise из палитры программирования
Выведите таблицы результатов и сравните их между собой.
Таблица 3
Варианты заданий
| № | Функция | x=[ ], a, b |
| 1. | 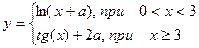 | x=[0 ..5] a=1.5 |
| 2. | 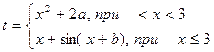 | x=[-2 ..2] a=5 b=2 |
| 3. | 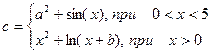 | x=[-5 ..5] a=2.5 b=3 |
| 4. | 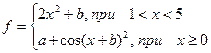 | x=[-4 ..4] a=3 b=1.5 |
| 5. | 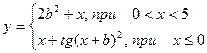 | x=[-3 ..4] a=6 b=3.5 |
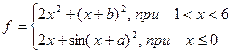 | x=[-2 .. 4] a=3 b=4 | |
| 6. | 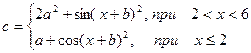 | x=[-4 5] a=2 b=1.5] |
Продолжение таблицы 3
| 7. | 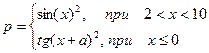 | x=[-5..5] a=3 b=4.5 |
| 8. | 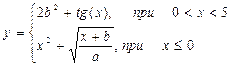 | x=[0..7] a=4 b=6 |
| 9. | 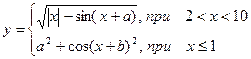 | x=[-1 .. 6] a=3 b=5 |
| 10. | 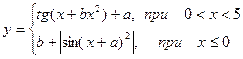 | x=[-2..7] a=2 b=4 |
| 11. | 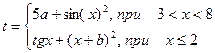 | x=[-1 5] a=3 b=8 |
| 12. | 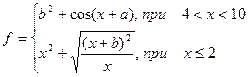 | x=[1 .. 8] a=2 b=4 |
| 13. | 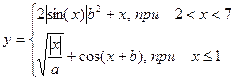 | x=[0…9] a=1.5 b=6 |
Методические указания
Для создания условных выражений можно использовать условия, функцию if , а также операторы программирования if и otherwise.
С помощью функции с элементами сравнения можно моделировать другие функции. Пример функции, описывающей импульсные сигналы различного вида, приведен на рис. 12.
Пример применения функции if
Пусть требуется найти значение функции
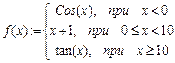 для x=7.
для x=7.
Mathcad-документ может быть составлен следующим образом:
f(x):= if(x<0,cos(x),if(x<10,x+1,tan(x))) f(7)= 8
Замечание: Функция f(x) может быть задана и таким образом:
f(x):=(x<0) cos(x)+(x>0) (x<10) (x+1)+(x>10) tan(x).
Для создания условия в Mathcad предусмотрены также операторы в палитре программирования if и otherwise (если, иначе).
На рис.12 приведен пример моделирования выпрямления функции sin(x).

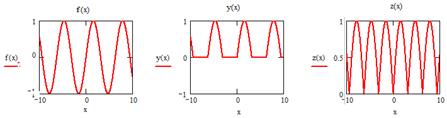
Рис. 12 Пример моделирования одно и двух–полупериодного
выпрямления функции
Контрольные вопросы
1. Какие виды встроенных функций имеются в системе Mathcad?
2. Как пользоваться встроенными функциями?
3. Запись условий в системе Mathcad.
4. Как записать условную функцию, используя условные выражения?
5. Синтаксис функции if, её аргументы?
6. Значения условного выражения при истинности условия?
7. Значения условного выражения при ложности условия?
Лабораторная работа №3
Функции для обработки векторов и матриц
Подготовка к работе
По указанной литературе изучить
- палитру Vector and Matrix (Векторы и матрицы) и назначение элементов этих палитр;
- ввод, вывод и обработку одномерных и двумерных массивов данных;
- приемы работы с массивами данных в Mathcad;
- векторные и матричные операторы;
- векторные и матричные функции;
Задание и порядок выполнения работы
1 Выполнить сортировку для векторов (Таблица 4)
2 Выполнить сортировку для матриц (Таблица 5).
3 Вычислить вектор VE собственных значений матрицы М .
Таблица 4
Варианты заданий
| № вар. | Заданный вектор | № вар. | Заданный вектор |
| V=[3, 2, 4, 5] | V=[7, 18, 3, 11] | ||
| V=[7, 8, 9, 5] | V=[1, 5, 3, 9] | ||
| V=[12, 14, 7, 11] | V=[24, 9, 12, 27] | ||
| V=[6, 8, 10, 15] | V=[9, 3, 17, 11] | ||
| V=[3, 9, 12, 14] | V=[4, 15, 2, 19] | ||
| V=[7, 9, 11, 13] | V=[11, 17, 1, 13] | ||
| V=[5, 7, 8, 12] | V=[5, 9, 15, 2] | ||
| V=[23, 25, 7, 19] |
Таблица 5
Варианты заданий
| № вар | Исходная матрица 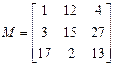 | № вар | Исходная матрица 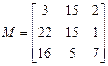 |
| Отсортировать по 1 столбцу. Вывести этот столбец | Отсортировать по 1 столбцу. Вывести этот столбец | ||
| Отсортировать по 1 строке. Вывести эту строку | Отсортировать по 1 строке. Вывести эту строку | ||
| Отсортировать по 2 столбцу. Вывести этот столбец | Отсортировать по 2 столбцу Вывести этот столбец |
Продолжение таблицы 5
| Отсортировать по 2 строке. Вывести эту строку | Отсортировать по 2 строке. Вывести эту строку | ||
| Отсортировать по 3 столбцу Вывести этот столбец | Отсортировать по 3 столбцу Вывести этот столбец | ||
| Отсортировать по 3 строке. Вывести эту строку | Отсортировать по 3 строке. Вывести эту строку |
Методические указания
Вывод элементов матрицы А и элементов вектора В и Х1
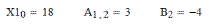
Транспонирование вектора Х
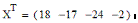
Исходный вектор Прямая сортировка Реверс сортировки
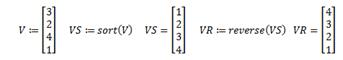
Исходная матрица Сортировка по первой строке Сортировка по первому столбцу
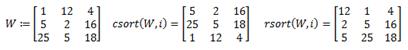
Начальный индекс столбца и строки ORIGIN = 0
Вывод второго столбца матрицы Вывод второй строки матрицы

Рис. 10 Примеры применения векторных и матричных функций
Контрольные вопросы
1. Какие операции можно производить с матрицами и векторами в Mathcad?
2. Назовите элементы палитры Vector and Matrix (Векторы и матрицы) и их назначение.
3. Назовите операции над матрицами и векторами в Mathcad?
4. Назовите функции сортировки векторов и матриц.
5. Как вывести нужный элемент массива?
6. Как вывести заданный столбец матрицы?
7. Как вывести заданную строку матрицы?
8. Назовите функцию вычисления следа матрицы, поясните, что называется следом матрицы.
Лабораторная работа №4
Решение систем линейных и нелинейных уравнений
Подготовка к работе
По указанной литературе изучить
- способы решения систем линейных уравнений в Mathcad;
- способы решения нелинейных уравнений в Mathcad
- функция для решения системы линейных уравнений методом Гаусса.
Задание и порядок выполнения работы
1. Решить систему линейных уравнений (Таблица 6):
- используя функцию Find, решить уравнение в символьном виде;
- матричным способом;
- используя функцию lsolve.
2. Решить систему нелинейных уравнений (Таблица 7)
- приближенно графически;
- используя функцию Find
- используя функцию Minerr.
Таблица 6
Варианты заданий
| № вар. | Система линейных уравнений | № вар. | Система линейных уравнений |
| 1. | 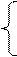 2x1 +x2 + 2x3+3x4=8 3x1+3x3=6 2x1 – x2 + 3x4=4 x1+2x2 – x3 + 2x4=4 2x1 +x2 + 2x3+3x4=8 3x1+3x3=6 2x1 – x2 + 3x4=4 x1+2x2 – x3 + 2x4=4 | 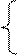 x1 +2x2 + 8x3+2x4= 114 8x1+x2 + 2x3 + x4=52 x1 + 5x2 + x3 =72 x1 – 12x2 +5x3 + x4= 97 x1 +2x2 + 8x3+2x4= 114 8x1+x2 + 2x3 + x4=52 x1 + 5x2 + x3 =72 x1 – 12x2 +5x3 + x4= 97 | |
| 2. | 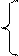 x1 +2x2 + 3x3+4x4=22 2x1+3x2+ x3 + 2x4=17 2x1 + x2 + x3 – 7x4=8 x1 – x3 + 3x4= – 7 x1 +2x2 + 3x3+4x4=22 2x1+3x2+ x3 + 2x4=17 2x1 + x2 + x3 – 7x4=8 x1 – x3 + 3x4= – 7 | 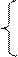 6x1 - 4x2 + 12x3 - 2x4= 132 2x1+x2 + 9x3 + 5x4=118 3x1 - 2x2 - 2x3 - x4=7 x1 - 12x2 +2x3 - x4= 17 6x1 - 4x2 + 12x3 - 2x4= 132 2x1+x2 + 9x3 + 5x4=118 3x1 - 2x2 - 2x3 - x4=7 x1 - 12x2 +2x3 - x4= 17 | |
| 3. | 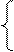 2x1 +x2 - 5x3+x4= – 4 x1+3x2 - 6x4=9 x1 – x2 + 3x3=6 x1+4x2 –7x3 + 2x4= – 2 2x1 +x2 - 5x3+x4= – 4 x1+3x2 - 6x4=9 x1 – x2 + 3x3=6 x1+4x2 –7x3 + 2x4= – 2 | 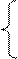 x1 - 2x2 - x4= 86 5x1 + 2x3 - 3x4=88 7x1 - 3x2 + 7x3 +2x4=146 3x1 – 7 x2 +6x3 + 3x4= 89 x1 - 2x2 - x4= 86 5x1 + 2x3 - 3x4=88 7x1 - 3x2 + 7x3 +2x4=146 3x1 – 7 x2 +6x3 + 3x4= 89 | |
| 4. | 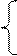 x1 +2x2 + 3x3+2x4= 24 2x1+3x2 + 4x3 + x4=32 3x1 + 4x2 + x3 +2x4=26 4x1+2x2 +x3 + 3x4= 24 x1 +2x2 + 3x3+2x4= 24 2x1+3x2 + 4x3 + x4=32 3x1 + 4x2 + x3 +2x4=26 4x1+2x2 +x3 + 3x4= 24 | 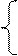 x1 - 2x2 - 8x4= – 8 x1+5x2 - 7x3 + 5x4= – 12 x1 + x2 - 5x3 +2x4= – 15 3x1 – x2 + 3x4= 9 x1 - 2x2 - 8x4= – 8 x1+5x2 - 7x3 + 5x4= – 12 x1 + x2 - 5x3 +2x4= – 15 3x1 – x2 + 3x4= 9 |
Продолжение таблицы 6
| 5. | 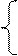 2x1 +x2 + 5x3 - x4= 14 7x2 - x3 + 3x4= – 5 4x1 + x2 + 2x3 =16 x1+5x2 +2x3 - 7x4= – 13 2x1 +x2 + 5x3 - x4= 14 7x2 - x3 + 3x4= – 5 4x1 + x2 + 2x3 =16 x1+5x2 +2x3 - 7x4= – 13 | 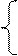 2x1 +2x2 + 7x3+x4= 14 – 2x2 + 3x3 + x4=19 2x1 + 2x2 + x3 +x4=22 3x1 - 5x2 +x3 - x4= 32 2x1 +2x2 + 7x3+x4= 14 – 2x2 + 3x3 + x4=19 2x1 + 2x2 + x3 +x4=22 3x1 - 5x2 +x3 - x4= 32 | |
| 6. | 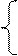 4x1 +7x2 + x3 - 4x4= 12 x1 + 6x3 + x4=21 x1 + 4x2 + 6x4=16 2x2 +4x3 + x4= 15 4x1 +7x2 + x3 - 4x4= 12 x1 + 6x3 + x4=21 x1 + 4x2 + 6x4=16 2x2 +4x3 + x4= 15 | 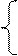 8x1 - x2 + 7x3+5x4= 156 2x1+x2 - 3x3 - x4= – 17 11x1 + 4x2 + x3 =176 x1 - x2 - 3x3 - 4x4= – 25 8x1 - x2 + 7x3+5x4= 156 2x1+x2 - 3x3 - x4= – 17 11x1 + 4x2 + x3 =176 x1 - x2 - 3x3 - 4x4= – 25 | |
| 7. | 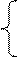 7x1 +7x2 - 3x3+2x4= 8 2x1+4x2 + 5x3 + 8x4=42 2x1 + 2x2 + 2x3 +2x4=28 2x1 - 2x3 - x4= – 2 7x1 +7x2 - 3x3+2x4= 8 2x1+4x2 + 5x3 + 8x4=42 2x1 + 2x2 + 2x3 +2x4=28 2x1 - 2x3 - x4= – 2 | 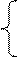 6x1 - 9x2 + 7x3= 75 7x1 - 3x3 - x4= – 35 9x2 + 7x3 +x4=97 5x1 - 9x2 +x3 + 6x4= 45 6x1 - 9x2 + 7x3= 75 7x1 - 3x3 - x4= – 35 9x2 + 7x3 +x4=97 5x1 - 9x2 +x3 + 6x4= 45 | |
| 8. |  6x1 - 7x2 + 5x3+2x4= 64 5x1+5x2 - 14x3 = – 27 4x1 + 3x2 – 11x4=6 x1+2x2 +2x3 + x4= 42 6x1 - 7x2 + 5x3+2x4= 64 5x1+5x2 - 14x3 = – 27 4x1 + 3x2 – 11x4=6 x1+2x2 +2x3 + x4= 42 |
Таблица 7
Варианты заданий
| № | Функции F1(x), F2(x) интервал x=[ ], шаг h | № | Функции F1, F2 интервал x=[ ], шаг h |
| 1. | F1(x)= – 1.5x3 – 5x2+3x+45 F2(x)= – 75│cos(x)│ x=[ – 10..10] h=0.3 | 9. | F1(x)=2.5x3 + 2.9x2+x+17 F2(x)= 20sin(x2) x=[ – 20..20] h=0.2 |
| 2. | F1(x)=5x3 + x2+12x+9 F2(x)= 25│sin(x)│(1) x=[ – 10..10] h=0.2 | 10. | F1(x)= – 3.5x3 +10x+65 F2(x)= 55│cos(x)│ x=[ – 10..10] h=0.3 |
| 3. | F1(x)=– 0.5x3 + 5x2+5x – 15 F2(x)= – 15│tg(x)│ x=[ – 10..10] h=0.1 | 11. | F1(x)=7.5x3 – x2 – 13x +35 F2(x)= 10│cos(x)│ x=[ – 10..10] h=0.3 |
| 4. | F1(x)=x3 + 2x2+15x – 27 F2(x)= 53│cos(x)│ x=[ – 15..15] h=0.5 | 12. | F1(x)=– 3x3 + x2 – 20x – 7 F2(x)= 20│tg(x)│ x=[ – 10..10] h=0.3 |
| 5. | F1(x)=4.6x2+10x + 30 F2(x)= 40sin(x) x=[ – 10..10] h=0.3 | 13. | F1(x)=6.5x3 – 9x2+7x – 19 F2(x)= – 15│tg(3x)│ x=[ – 15..15] h=0.1 |
| 6. | F1(x)=– 4.5x3 + 3x2 – 4 x+60 F2(x)= 90│cos(x)│ x=[ – 20..20] h=0.4 | 14. | F1(x)=– 8.5x3 – 2x2+20x+5 F2(x)= – 35│cos(x)│ x=[ – 10..10] h=0.2 |
| 7. | F1(x)=– 7.5x3 + 16x2+54 F2(x)= – 45│cos(2x)│ x=[ – 25..20] h=0.2 | 15. | F1(x)= – 15x2+9x+70 F2(x)= 5│sin(x)│ x=[ – 20..20] h=0.5 |
| 8. | F1(x)=– 5x3 +13x+40 F2(x)= 50cos(3x) x=[ – 10..10] h=0.5 |
Методические указания
Решить систему линейных уравнений: 
4x1 +x2 + x3+3x4=25
3x1 – x2+3x3=16
2x1 – 2x2 + 3x4=– 4
x1+2x2 – x3 + 2x4=4
Матричным способом X:=A-1 × B, где А- матрица, составленная из коэффициентов перед неизвестными, В – вектор свободных членов, X – вектор корней x1, x2, x3 …;
С помощью встроенной функции lsolve(А,В).
Проверить результаты решения непосредственной подстановкой полученных корней х1, х2, х3 в одно из заданных уравнений.
Решение в матричной форме
А – матрица коэффициентов системы при неизвестных
В – вектор свободных членов
Решение системы в матричной форме A × Х:=В, где Х – вектор корней системы линейных уравнений.
Результат решения системы линейных уравнений Х=(х1,х2,х3,х4)
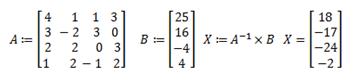
Результат решения системы линейных уравнений Х1=(x1,х2,х3,х4)
Результат решения системы линейных уравнений с использованием функции lsolve

Проверка решения системы линейных уравнений