Скалярное произведение двух векторов
| Свойства |
| Определение |
| Применение |
Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними: 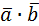 =| =| 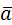 || || 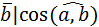 |
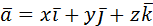 | | 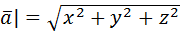 |
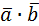 = = 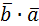 |

k( 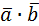 )= = (k )= = (k 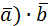 = = = = 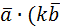 ) ) |
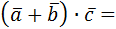 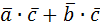 |
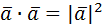 |
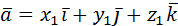 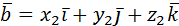 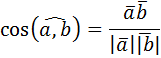 |
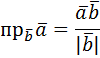 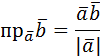 |
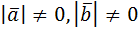 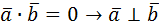 |
Работа силы F на перемещение S А= 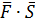 |
Вычисление в прямоугольных координатах: если 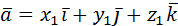 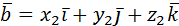 , то , то 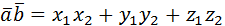 . . |
Скалярное произведение ортов 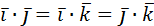 =0 =0 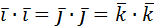 =1 =1 |
Примеры решения типовых задач
1. Даны векторы 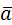 =3
=3 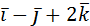 и
и 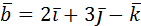 . Найти: а)
. Найти: а) 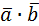 ;
;
б) 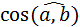 ; в)
; в) 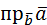 .
.
Решение:
а) 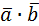 =3∙2+(-1)3+2(-1)=6-3-2=1;
=3∙2+(-1)3+2(-1)=6-3-2=1;
б) 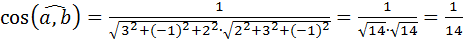 ;
;
в) 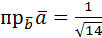 .
.
Ответ: а) 1; б)  ; в)
; в) 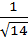 .
.
2. Даны векторы 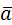 {3;-1;4},
{3;-1;4}, 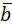 {-2;2;2}. Проверить, являются ли они ортогональными.
{-2;2;2}. Проверить, являются ли они ортогональными.
Решение:
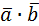 =3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы
=3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы 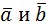 ортогональны.
ортогональны.
3. Вычислить работу силы 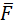 ={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
Решение:
А= 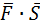 . Найдем координаты вектора
. Найдем координаты вектора 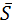 =
= 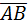 :
:
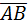 {4-2;2-4;7-6};
{4-2;2-4;7-6};
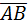 ={2;-2;1}.
={2;-2;1}.
Найдем работу А:
А=3∙2+2(-2)+4∙1=6-4+4=6.
Ответ: 6.
4. Найти длины диагоналей параллелограмма (рис.1), построенного на векторах 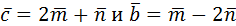 , где
, где 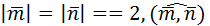 =60˚.
=60˚.
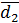 |
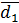 |
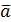
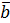 |
| Рис.1 |
Решение:
Выразим диагонали параллелограмма 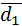 и
и 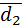 по правилу
по правилу
параллелограмма: 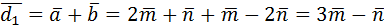 ,
,
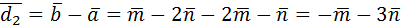 .
.
Так как векторы 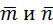 не единичные, следовательно,
не единичные, следовательно, 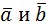 заданы в произвольном базисе, то
заданы в произвольном базисе, то 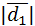 и
и 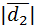 можно найти по определению:
можно найти по определению:
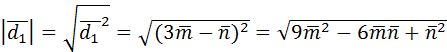 =
=
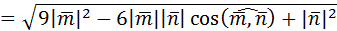 =
= 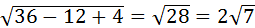 .
.
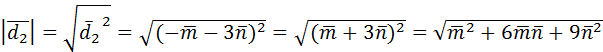 =
=
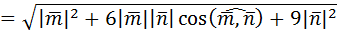 =
= 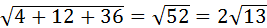 .
.
Ответ: 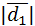 =
= 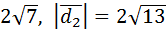 .
.
A. Векторное произведение двух векторов
| Свойства |
| Определение |
| Применение |
Площадь треугольника S= 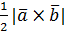 |
Векторным произведением двух векторов называется вектор 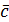 , длина которого численно равна площади параллелограмма, построенного на векторах , длина которого численно равна площади параллелограмма, построенного на векторах 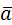 и и 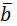 и направлен так, что кратчай-ший поворот от и направлен так, что кратчай-ший поворот от 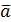 к к 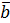 видится против часовой стрелки видится против часовой стрелки |
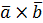 = = 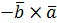 |

Вычисление 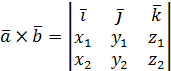 |
Условие коллинеарности 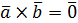 |
Момент силы 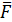 , в точке А относительно точки О: , в точке А относительно точки О: 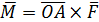 |
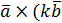 )= = k( )= = k( 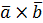 ) ) |
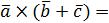 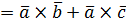 |
Примеры решения типовых задач
1. Раскрыть скобки и упростить выражение:
а) 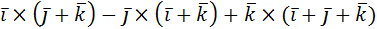 ;
;
б) (2 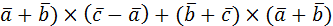 .
.
Решение:
а) 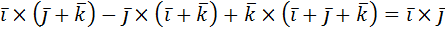 +
+ 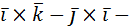
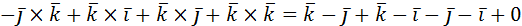 =2
=2 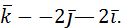
б) (2 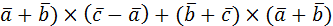 =2
=2 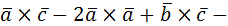
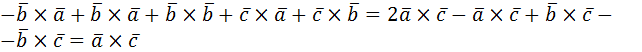 .
.
2. Даны векторы 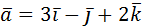 и
и 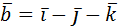 . Найти
. Найти 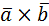 .
.
Решение:
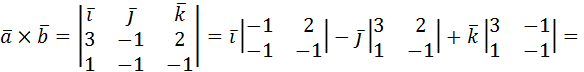
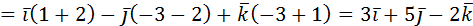 .
.
Ответ: 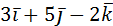 .
.
3. Найти площадь ∆АВС, если А(1;2;0); В(3;0;-3); С(5;2;6).
Решение:
S∆АВС= 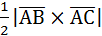 . Найдем координаты векторов
. Найдем координаты векторов 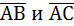 :
:
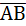 {3-1;0-2;-3-0}={2;-2;-3};
{3-1;0-2;-3-0}={2;-2;-3};
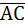 {5-1;2-2;6-0}={4;0;6}.
{5-1;2-2;6-0}={4;0;6}.
Найдем векторное произведение 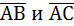 :
:
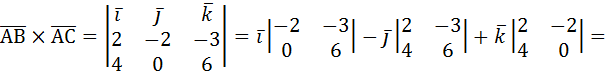
= 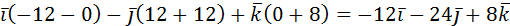 .
.
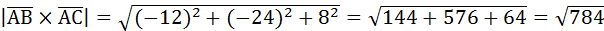 .
.
S∆АВС= 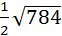 .
.
Ответ: 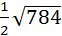 .
.
4. Сила 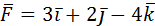 приложена в точке М(2;-1;1). Найти ее
приложена в точке М(2;-1;1). Найти ее
момент относительно начала координат.
Решение:
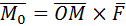 . Найдем координаты вектора
. Найдем координаты вектора 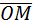 : О(0;0;0), М(2;-1;1), следовательно,
: О(0;0;0), М(2;-1;1), следовательно, 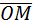 {2;-1;1}.
{2;-1;1}.
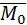 =
= 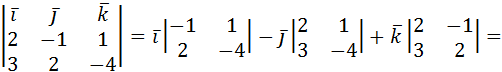
= 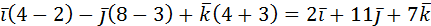 .
.
Ответ: 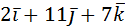 .
.
Смешанное произведение трех векторов
| Свойства |
| Определение |
| Применение |
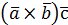 = = 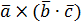 |
Объем параллелепипеда V= 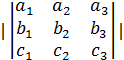 |
Смешанным произведением трех векторов называется произведение вида ( 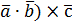 = = 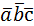 |

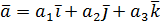 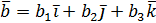 , , 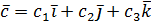 , то , то 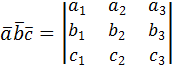 |
Объем пирамиды V= 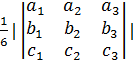 |
Условие компланарности трех векторов: 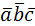 =0 =0 |
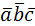 = = 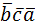 = = = = 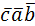 = = 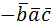 = = 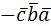 = = 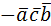 |
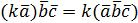 |
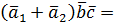 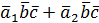 |
Примеры решения типовых задач
1. Найти объем пирамиды, вершинами которой служат точки
А(1;2;3); В(0;-1;1); С(2;5;2); D(3;0;-2).
Решение:
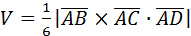 . Найдем координаты векторов
. Найдем координаты векторов 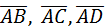 :
:
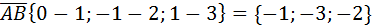 ;
;
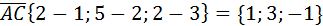 ;
;
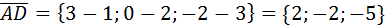 .
.
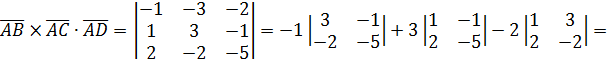
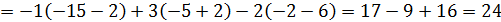 .
.
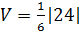 =4.
=4.
Ответ: 4.
2. Доказать, что векторы 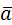 =2
=2 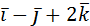 ,
, 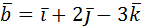 и
и 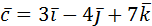 компланарны.
компланарны.
Доказательство:
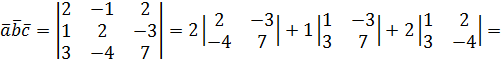
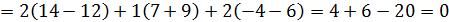 ,следовательно,
,следовательно, 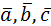 компланарны.
компланарны.
3. Проверить, лежат ли точки А(2;-1;-2), В(1;2;1), С(2;3;0), D(5;0;6) в одной плоскости.
Решение:
Для того чтобы доказать, что точки А, В, С, D лежат в одной плоскости, нужно доказать, что векторы 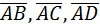 компланарны. Найдем координаты векторов
компланарны. Найдем координаты векторов 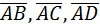 :
:
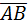 {1-2;2-(-1);1-(-2)}={-1;3;3};
{1-2;2-(-1);1-(-2)}={-1;3;3};
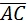 {2-2;3-(-1);0-(-2)}={0;4;2};
{2-2;3-(-1);0-(-2)}={0;4;2};
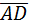 {5-2;0-(-1);6-(-2)}={3;1;8}.
{5-2;0-(-1);6-(-2)}={3;1;8}.
Проверим компланарность векторов 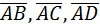 :
:
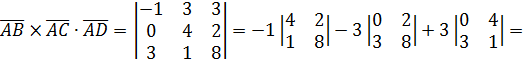
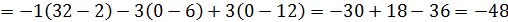 , следовательно, векторы
, следовательно, векторы 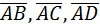 не компланарны, таким образом, точки А, В, С, D не лежат в одной плоскости.
не компланарны, таким образом, точки А, В, С, D не лежат в одной плоскости.
4. Даны координаты вершин пирамиды А(1;2;-3), В(1;0;-1), С(2;4; -6), D(0;-1;3). Найти а) VАВСD; б) S∆АВС; в) 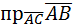 ; г)
; г) 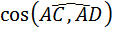 .
.
Решение:
а)VАВСD= 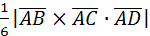 . Найдем координаты векторов
. Найдем координаты векторов 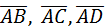 :
:
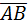 {1-1;0-2;-1(-3)}={0;-2;-2};
{1-1;0-2;-1(-3)}={0;-2;-2};
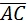 {2-1;4-2;-6-(-3)}={1;2;-3};
{2-1;4-2;-6-(-3)}={1;2;-3};
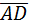 {0-1;-1-2;3-(-3)}={-1;-3;6}.
{0-1;-1-2;3-(-3)}={-1;-3;6}.
Найдем смешанное произведение 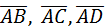 :
:
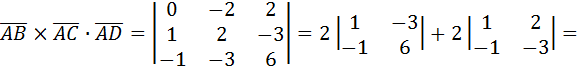
=2(6-3)=2(-3+2)=6-2=4.
Итак, VАВСD= 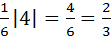 (куб.ед.).
(куб.ед.).
б) S∆АВС= 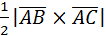 . Найдем векторное произведение векторов
. Найдем векторное произведение векторов 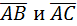 :
:
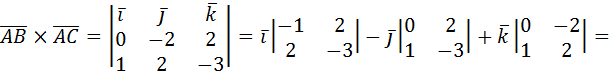
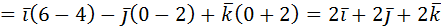 .
.
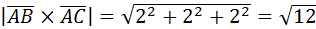 .
.
S∆АВС= 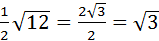 (кв.ед.)
(кв.ед.)
в) 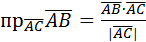 .
.
Найдем скалярное произведение векторов 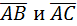 :
:
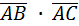 =0∙1+(-2)2+2(-2)=0-4-6=-10.
=0∙1+(-2)2+2(-2)=0-4-6=-10.
Найдем длину | 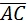 |=
|= 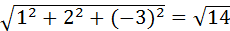 .
.
Итак, 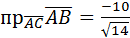 .
.
г) 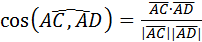 .Найдем скалярное произведение
.Найдем скалярное произведение 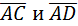 :
:
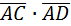 =1(-1)+2(-3)+(-3)6=-1-6-18=-25.
=1(-1)+2(-3)+(-3)6=-1-6-18=-25.
Найдем длину 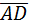 :
:
| 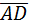 |=
|= 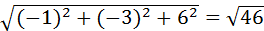 . Значит,
. Значит, 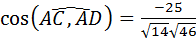 .
.
Ответ: а) 2/3 куб.ед.; б) 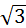 кв.ед. в)
кв.ед. в) 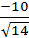 ; г)
; г) 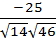 .
.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1.Найти длину вектора 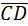 , если: С(1;-3;4), D(0;-2;1).
, если: С(1;-3;4), D(0;-2;1).
Ответ: | 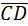 |=
|= 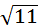 .
.
2. Найти длину радиус-вектора точки М(2;-3;6).
Ответ: 7.
3. Найти длину вектора 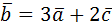 , если
, если 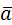 {2;-1;0},
{2;-1;0}, 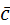 {3;-1;4}.
{3;-1;4}.
Ответ: 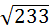 .
.
4.Найти направляющие косинусы вектора 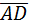 , если А(3;-5;4); D(2;-1;0).
, если А(3;-5;4); D(2;-1;0).
Ответ: cosα= 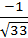 : cos
: cos 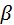 =
= 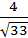 : cosγ=
: cosγ= 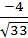 .
.
5. Даны векторы 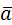 =2
=2 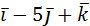 и
и 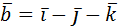 . Найти: а)
. Найти: а) 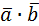 ; б)
; б) 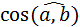 ; в)
; в) 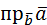 .
.
Ответ: а) 5; б) 5/9; в) 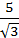 .
.
6. Даны векторы 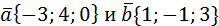 . Проверить, являются ли они ортогональными.
. Проверить, являются ли они ортогональными.
Ответ: не являются.
7. Вычислить работу силы 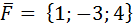 , если точка ее приложения перемещается прямолинейно из начала координат в положение М(1;-1;3).
, если точка ее приложения перемещается прямолинейно из начала координат в положение М(1;-1;3).
Ответ: 16.
8. Раскрыть скобки и упростить выражение:
1) 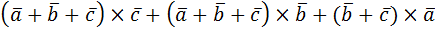 ;
;
2) 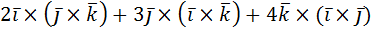 .
.
Ответ: 1) 2 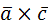 ; 2) 3.
; 2) 3.
9. Даны векторы 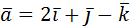 и
и 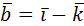 . Найти
. Найти 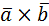 .
.
Ответ: 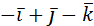 .
.
10. Найти площадь параллелограмма АВСD, если его вершины А(3;-2;4), В(0;-1;6), С(1;-3;6), D(1;-1;0).
Ответ: 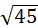 .
.
11. Сила 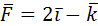 приложена в точке А(1;-1;0). Найти ее момент относительно точки В(2;-1;3).
приложена в точке А(1;-1;0). Найти ее момент относительно точки В(2;-1;3).
12. Проверить компланарность векторов 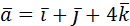 ,
,
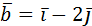 ,
, 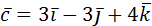 .
.
Ответ: компланарны.
13. Даны координаты вершин пирамиды А(4;4;10), В(7;10;2), С(2;8;4), D(9;6;9).
Найти: а) VАВСD; б) S∆АВС; в) 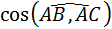 ; г)
; г) 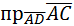 .
.
Ответ: а) 4; б) 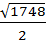 ; в)
; в) 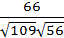 ; г)
; г) 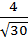 .
.
14. Найти угол между векторами 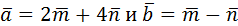 , где
, где 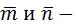 единичные векторы и угол между ними равен 120˚.
единичные векторы и угол между ними равен 120˚.
Ответ: -1/2.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Прямая линия на плоскости
Уравнением линии на плоскости ХОУ называется такое уравнение F(x,y)=0 с двумя переменными, которому удовлетворяют координаты х и у каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на линии.
Переменные х и у в уравнении линии называются текущими координатами точек линии.
Простейшей из линий является прямая.
Разным способам задания прямой соответствуют в прямоугольной системе координат различные виды ее уравнений (табл. 1).
Таблица 1
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечания |
| Уравнение с угловым коэффициентом y=kx+b | k – тангенс угла a наклона прямой к положительному направлению оси ОХ; b – отрезок, отсекаемый прямой от оси ОY | a≠π/2 | |
| Общее уравнение прямойАх+Ву+С=0 | А,В – координаты вектора, перпендикулярного прямой (нормального вектора) N | А,В не равны нулю одновременно | |
| Уравнение прямой, про-ходящей через данную точку в данном направ-ленииу-у0=k(х-х0 ) | т.М(х0,у0) – заданная точка; k – угловой коэффициент прямой | При различных k уравнение называется уравнением пучка прямых с центром в точке М(х0,у0) | |
Уравнение прямой, проходящей через две заданные точки 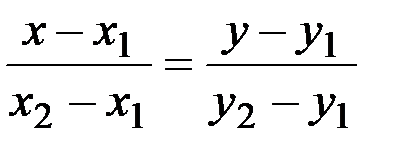 | т.М1(х1,у1), т.М2(х2,у2) – заданные точки | - | |
Уравнение прямой в отрезках на осях х 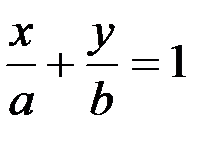 | а,b – отрезки, отсекаемые прямой от координатных осей ОХ и ОY соответственно | а≠0, b≠0 | |
| Уравнение прямой, проходящей через заданную точку параллельно заданному вектору | т.М0(х0,у0) – заданная точка; m,n – координаты вектора, параллельного искомой прямой ( направляющего век-тора)  | Такое уравнение часто называют каноническим | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечания |
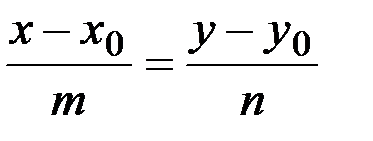 | |||
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору А(х-х0)+В(у-у0)=0 | т.М0(х0,у0) – заданная точка, А,В – координаты нормального вектора искомой прямой 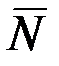 |
Угол между двумя прямыми
Пусть прямые l1и l2 заданы своими уравнениями с угловыми коэффициентами: l1: y=k1х+b1, l2:y=k2x+b2, тогда острый угол между двумя прямыми определяется его тангенсом по формуле
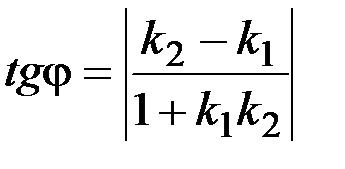 .
.
Если прямые l1и l2 заданы общими уравнениями А1х+В1у+С1=0 и А2х+В2у+С2=0, то угол между ними можно найти как угол между их нормальными векторами
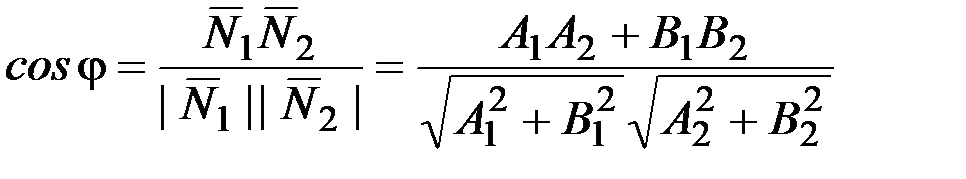 .
.
В случае задания прямых своими каноническими уравнениями
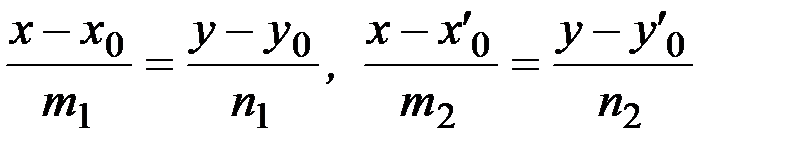 угол между прямыми находится как угол между направляющими векторами прямых
угол между прямыми находится как угол между направляющими векторами прямых
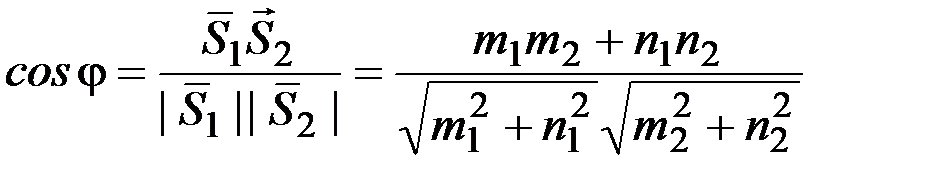 .
.
Условия параллельности и перпендикулярности прямых (табл. 2)
Таблица 2
| № п/п | Способ задания прямых | Условие параллельности прямых | Условие перпендикулярности прямых |
| l1: y=k1х+b, l2: y=k2x+b2 | k1=k2 | k1k2= -1 | |
| l1: А1х+В1у+С1=0 l2: А2х+В2у+С2=0 | 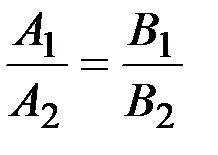 | A1A2+B1B2=0 | |
l1: 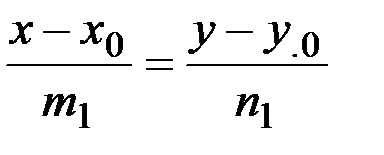 l2: l2: 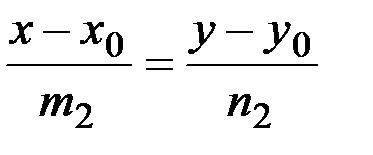 | 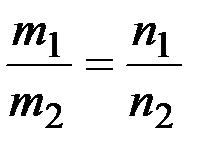 | m1m2+n1n2=0 |
