Множества и операции над ними
Множества и операции над ними
Понятие множества
Теория множеств опирается на три первичных понятия:
1) множество;
2) элемент;
3) принадлежность.
Строгого определения этим понятиям не дается, описывается только их применение. Для этих понятий используются обозначения: “ 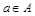 ”- элемент а принадлежит множеству А; “
”- элемент а принадлежит множеству А; “ 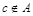 ”элемент с не принадлежит множеству А.
”элемент с не принадлежит множеству А.
Говоря о некотором множестве, мы требуем его:
1) целостности, т.е. возможности рассматривать его как отдельный объект;
2) различимости его элементов;
3) неупорядоченности элементов.
Поэтому записи 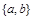 и
и 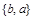 определяют одно и то же множество.
определяют одно и то же множество.
1.1.2. Способы задания множеств
Множество можно задать, перечислив все его элементы: 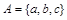 ,
, 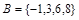 . Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.
. Порядок записи элементов множества произволен. Часто задают множество, указав его характеристическое свойство, которое для каждого элемента позволяет выяснить, принадлежит он множеству или нет.
Например,
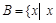 – целый корень уравнения
– целый корень уравнения 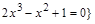 ,
,
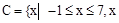 – целое }.
– целое }.
В дальнейшем для известных числовых множеств будут использоваться обозначения:
N = { 1,2,3,…} – множество натуральных чисел;
Z = { …, -2,-1,0,1,2,…} – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
1.1.3. Основные определения
Пустым множеством называется множество Æ, не содержащее ни одного элемента, т.е. для любого элемента x выполняется 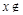 Æ.
Æ.
Универсальным называется множество U всех элементов, рассматриваемых в данной задаче.
Пример. Пусть U = Z и требуется найти все решения уравнения 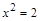 . Множество М решений этой задачи есть пустое множество: М = Æ.
. Множество М решений этой задачи есть пустое множество: М = Æ.
Пусть теперь U = R. Тогда множество М решений уравнения 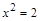 не пусто: М =
не пусто: М = 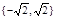 .
.
Будем говорить, что множество А включается во множество В 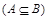 , если каждый элемент множества А является элементом множества В ( говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
, если каждый элемент множества А является элементом множества В ( говорят также, что А является подмножеством множества В). Из определения включения следуют свойства:
1) 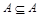 для любого множества А;
для любого множества А;
2) Если 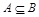 и
и 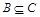 , то
, то 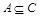 ;
;
3) Æ 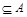 для любого множества А;
для любого множества А;
4) 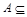 U для любого множества А.
U для любого множества А.
Подмножество 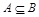 называется собственным подмножеством множества В (
называется собственным подмножеством множества В ( 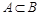 - строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N
- строгое включение), если А не пусто и не совпадает с В. Например, имеют место строгие включения: N  Z
Z  Q
Q 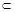 R.
R.
Определим понятие равенства множеств: А=В тогда и только тогда, когда одновременно выполняются два включения 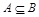 и
и 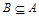 , т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:
, т.е. каждый элемент множества А является элементом множества В и каждый элемент множества В является элементом множества А:
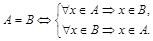
Свойства равенства множеств:
1) для любого А справедливо А=A;
2) если А=В, то и В=A;
3) если А=В и В=C, то A=C.
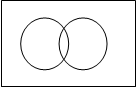
Диаграммы Эйлера – Венна
Эти диаграммы применяются для наглядного изображения множеств и их взаимного расположения.
 |
U
A B
Рис. 1.1 Диаграмма Эйлера-Венна
Универсальное множество U изображается в виде прямоугольника, а произвольные множества – подмножества универсального – в виде кругов (рис. 1.1).
При этом возможны следующие случаи взаимного расположения двух множеств А и В:
1) одно из множеств строго включается в другое ( 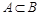 или
или 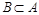 );
);
2) множества равны;
3) множества не имеют общих элементов;
4) множества находятся в общем положении, т.е. не подходит ни один из вышеперечисленных случаев, и множества расположены как на рис. 1.1.
Операции над множествами
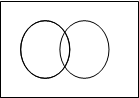
Объединением множеств А и В называется множество 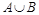 , состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В (рис. 1.2, а).
, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В (рис. 1.2, а).
Пример. Если 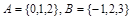 , то
, то 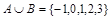 .
.





 U U
U U

A B A B
а) б)
Рис. 1.2. Операции над множествами:
а) объединение множеств;
б) пересечение множеств
Пересечением множеств А и В называется множество 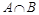 , состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству А, и множеству В (рис. 1.2, б).
, состоящее из тех и только тех элементов, которые принадлежат одновременно и множеству А, и множеству В (рис. 1.2, б).
Пример. Если 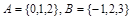 , то
, то 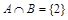 .
.
Разностью множеств А и В называется множество 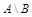 тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В (рис. 1.3, а).
тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В (рис. 1.3, а).
Пример. 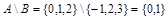 ;
;
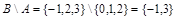 .
.
Дополнением множества А до универсального U называется множество 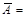 U
U 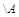 (рис. 1.3, б).
(рис. 1.3, б).
Пример. Если 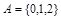 ,U
,U 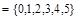 , то
, то 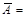 U
U 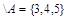 .
.

U U
A B
A
а) б)
Рис. 1.3. Операции над множествами:
а) разность множеств A и B;
б) дополнение множества A
Системы множеств
Элементы множества сами могут быть множествами: 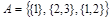 ; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан, разбиение и покрытие множеств.
; в таком случае удобно говорить о системе множеств. Рассмотрим такие системы множеств, как булеан, разбиение и покрытие множеств.
Булеаном B(Х) множества Х называется множество всех подмножеств множества Х. Например, для множества 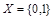 булеаном является множество B
булеаном является множество B 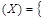 Æ,
Æ, 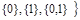 .
.
Разбиением R(Х) множества Х называется система его непустых непересекающихся подмножеств, в объединении дающая множество Х (рис. 1.4).





U
X X1 X2
X3 X4
Рис. 1.4. Разбиение множества R 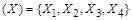
Например, для множества 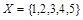 можно построить разбиение R1
можно построить разбиение R1 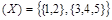 , состоящее из двух элементов (они называются блоками разбиения), или разбиение R2
, состоящее из двух элементов (они называются блоками разбиения), или разбиение R2  – из четырех блоков; возможны и другие разбиения этого множества Х.
– из четырех блоков; возможны и другие разбиения этого множества Х.
Покрытием P(X) множества X называется система его непустых подмножеств, в объединении дающая множество X (рис. 1.5).
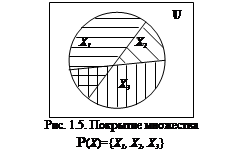 |
В этом определении отсутствует слово “непересекающаяся” – т.е. блоки могут иметь общие элементы.
Пример. Для множества 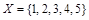 покрытиями являются системы множеств
покрытиями являются системы множеств 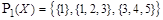 и
и 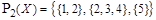 .
.
1.1.7. Законы алгебры множеств
Так же, как операции обычной алгебры, операции над множествами выполняются по законам (табл. 1.1), которые доказываются на основе введенных выше определений. Особенностью алгебры множеств является закон идемпотентности, благодаря которому в алгебре множеств нет числовых коэффициентов и степеней.
Таблица 1.1
Законы алгебры множеств
| № | Формулы | Название |
AÇÆ =Æ ; AÈÆ = A; AÇ 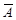 =Æ =Æ | Свойства пустого множества | |
| AÈU = U; AÇU = A; AÈĀ = U | Свойства универсального множества | |
| AÇB = BÇA; AÈB = BÈA | Закон коммутативности | |
| (АÇВ)ÇС=АÇ(ВÇС); (АÈВ)ÈС=АÈ(ВÈС) | Закон ассоциативности | |
| АÇ(ВÈС)= (АÇВ)È(АÇС); АÈ(ВÇС)= (АÈВ)Ç(АÈС) | Закон дистрибутивности | |
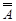 =А =А | Закон двойного дополнения | |
| АÇА=А; АÈА=А | Законы идемпотентности | |
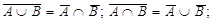 | Законы де Моргана | |
| АÈ(АÇВ)=А; АÇ(АÈВ)=А | Законы поглощения |
Докажем закон дистрибутивности
АÈ(ВÇС)= (АÈВ)Ç(АÈС). (1.1)
Обозначим X левую часть равенства (1.1), Y – правую. Согласно определению равенства множеств покажем, что выполняются одновременно 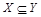 и
и 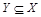 .
.
Пусть x – произвольная точка из множества X=АÈ(ВÇС). Тогда по определению объединения множеств ( 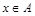 или
или 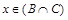 ). Далее по определению пересечения множеств (
). Далее по определению пересечения множеств ( 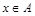 или
или 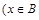 и
и 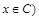 ). Следовательно,
). Следовательно,
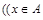 или
или 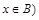 и (
и ( 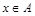 или
или 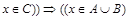 и
и 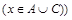
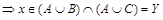
Таким образом для любого 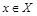 выполняется
выполняется 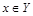 , т.е.
, т.е. 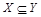 .
.
Докажем теперь, что 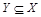 . Пусть y – произвольная точка из множества
. Пусть y – произвольная точка из множества 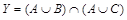 . Тогда
. Тогда
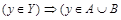 и
и 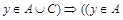 или
или 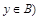 и
и 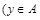 или
или
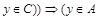 или
или 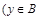 и
и 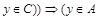 или
или 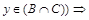
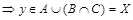 .
.
В силу произвольности 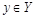 заключаем
заключаем 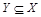 .
.
Таким образом, 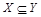 и
и 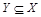 , следовательно,
, следовательно, 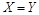 , и закон дистрибутивности доказан.
, и закон дистрибутивности доказан.
Бинарные отношения
Свойства бинарных отношений
Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают. Рассмотрим следующие отношения на множестве 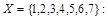
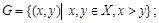
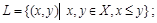
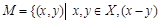 делится на
делится на 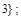
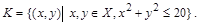
Отношение R на множестве Х называется рефлексивным,если для всех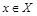 выполняется условие
выполняется условие 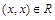 . Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство
. Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство 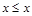 справедливо при всех
справедливо при всех 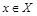 ) и отношение М (т.к. разность
) и отношение М (т.к. разность 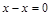 делится на 3, значит, пара
делится на 3, значит, пара 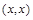 принадлежит отношению М при всех
принадлежит отношению М при всех 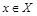 ).
).
Отношение R на множестве Х называется антирефлексивным, если условие 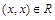 не выполняется ни при одном
не выполняется ни при одном 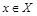 . Примером антирефлексивного отношения является отношение G (неравенство
. Примером антирефлексивного отношения является отношение G (неравенство 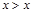 не выполняется ни при каких значениях х, следовательно, ни одна пара
не выполняется ни при каких значениях х, следовательно, ни одна пара 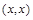 не принадлежит отношению G). Отметим, что отношение К не является рефлексивным
не принадлежит отношению G). Отметим, что отношение К не является рефлексивным 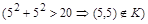 и не является антирефлексивным
и не является антирефлексивным 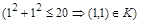 .
.
Отношение R на множестве Х называется симметричным, если из условия 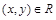 следует
следует 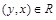 . Симметричными являются отношения М (если
. Симметричными являются отношения М (если 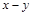 делится на 3, то и
делится на 3, то и 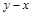 делится на 3) и К (если
делится на 3) и К (если 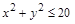 , то и
, то и 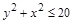 ).
).
Отношение R на множестве Х называется несимметричным, если для любых 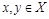 из условия
из условия 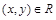 следует
следует 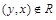 . Несимметричным является отношение G, т.к. условия
. Несимметричным является отношение G, т.к. условия 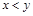 и
и 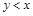 не могут выполняться одновременно (только одна из пар
не могут выполняться одновременно (только одна из пар 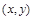 или
или 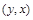 принадлежит отношению G).
принадлежит отношению G).
Отношение R на множестве Х называется антисимметричным, если для любых 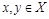 из условия
из условия 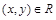 и
и 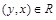 следует
следует 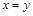 . Антисимметричным является отношение L, т.к. из одновременного выполнения
. Антисимметричным является отношение L, т.к. из одновременного выполнения 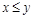 и
и 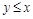 следует
следует 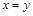 .
.
Отношение R на множестве Х называется транзитивным, если для любых  из одновременного выполнения условий
из одновременного выполнения условий 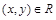 и
и 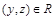 следует
следует 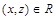 . Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если
. Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если 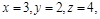 то
то 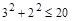 и
и 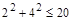 , но
, но 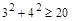 , то есть выполняются условия
, то есть выполняются условия 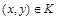 и
и 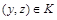 , но
, но 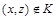 .
.
Отношения эквивалентности
Рассмотрим три отношения: M, S, H. Отношение М описано в 1.2.4. Отношение S введем на множестве X всех треугольников следующим образом: этому отношению принадлежат пары треугольников такие, что площадь треугольника x равна площади треугольника y.
Отношение Н действует на множестве жителей г. Томска и содержит пары 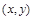 такие, что х и у носят шляпы одинакового размера.
такие, что х и у носят шляпы одинакового размера.
Свойства этих трех отношений приведены в таблице 1.3, где Р означает рефлексивность, АР – антирефлексивность, С – симметричность, АС - антисимметричность, НС – несимметричность, Т – транзитивность отношения. В качестве упражнения проверьте правильность заполнения таблицы, пользуясь определениями свойств бинарных отношений.
Таблица 1.3
Свойства отношений
| Отношение | Р | АР | С | АС | НС | Т |
| М | + | - | + | - | - | + |
| S | + | - | + | - | - | + |
| H | + | - | + | - | - | + |
Мы видим, что отношения обладают одинаковыми свойствами, поэтому их относят к одному типу.
Определение. Отношение R на множестве Х называется отношением эквивалентности, если оно обладает свойствами рефлексивности, симметричности, транзитивности.
Таким образом, отношения M, S, H являются отношениями эквивалентности на соответствующих множествах Х. Важной особенностью отношений эквивалентности является то, что они разбивают все множество Х на непересекающиеся подмножества – классы эквивалентности.
Определение. Классом эквивалентности, порожденным элементом 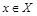 , называется подмножество
, называется подмножество 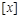 множества Х, для элементов которого выполняется условие
множества Х, для элементов которого выполняется условие 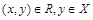 . Таким образом, класс эквивалентности
. Таким образом, класс эквивалентности 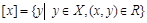 .
.
Так, отношение М разбивает множество 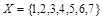 на три класса эквивалентности:
на три класса эквивалентности: 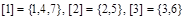 . Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
. Класс, порожденный элементом 4, совпадает с классом [1]; [5] = [2], [3] = [6], [7] = [1].
Классы эквивалентности образуют систему непустых непересекающихся подмножеств множества Х, в объединении дающую все множество Х – т.е. образуют разбиение множества Х (см. 1.1.6).
Отношение эквивалентности обозначают “ º “, поэтому определение класса эквивалентности можно записать так: 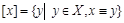 .
.
Множество различных классов эквивалентности множества X по отношению R называется фактор-множеством и обозначается 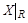 . Так, для отношения M фактор-множество состоит из трех элементов:
. Так, для отношения M фактор-множество состоит из трех элементов:
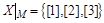 .
.
Теорема 1. Пусть R – отношение эквивалентности на множестве X и 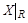 - совокупность всех различных классов эквивалентности по отношению R. Тогда
- совокупность всех различных классов эквивалентности по отношению R. Тогда 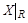 - разбиение множества X.
- разбиение множества X.
Доказательство. По условию теоремы R – отношение эквивалентности, т.е. рефлексивно, симметрично и транзитивно. Покажем, что 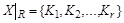 - разбиение множества X, т.е.
- разбиение множества X, т.е.
а) 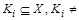 Æ;
Æ;
б) 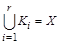 ;
;
в) 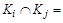 Æ,
Æ, 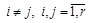 .
.
Условие а выполняется по определению класса эквивалентности и по свойству рефлексивности, т.к. 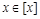 для любого
для любого 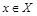 .
.
Условие б выполняется, так как каждый элемент множества X попадает в какой-либо класс эквивалентности и 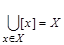 .
.
Условие в докажем методом “от противного”. Пусть 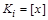 и
и 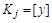 - разные классы эквивалентности (т.е.
- разные классы эквивалентности (т.е. 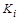 и
и 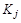 отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент
отличаются хотя бы одним элементом). Покажем, что они не пересекаются. Предположим противное: найдется элемент 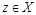 такой, что
такой, что 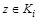 и
и 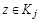 . По определению класса эквивалентности
. По определению класса эквивалентности 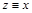 и
и 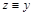 . По свойствам симметричности и транзитивности отношения R имеем:
. По свойствам симметричности и транзитивности отношения R имеем: 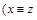 и
и 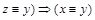 - отсюда следует равенство множеств
- отсюда следует равенство множеств 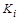 и
и 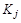 .
.
Действительно, возьмем произвольный элемент 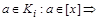
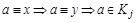 в силу произвольности a следует
в силу произвольности a следует 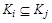 . Возьмем произвольный элемент
. Возьмем произвольный элемент 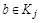 :
: 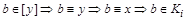 - в силу произвольности b следует
- в силу произвольности b следует 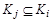 . По определению равенства множеств
. По определению равенства множеств 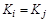 .
.
Условие в доказано: если классы эквивалентности не совпадают, то они не пересекаются.
Следовательно, фактор-множество 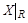 является разбиением множества X.
является разбиением множества X.
Теорема 2. Всякое разбиение множества X порождает на X отношение эквивалентности.
Доказательство. Пусть 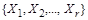 - разбиение множества X. Рассмотрим на X отношение
- разбиение множества X. Рассмотрим на X отношение 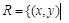 найдется
найдется 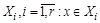 и
и 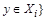 .
.
Покажем, что R – отношение эквивалентности.
Рефлексивность отношения R следует из условия 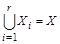 . Каждый элемент множества X попадает в одно из множеств
. Каждый элемент множества X попадает в одно из множеств 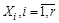 , поэтому
, поэтому 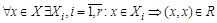 .
.
Покажем, что отношение R симметрично. Пусть 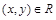 . Это означает, что
. Это означает, что
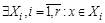 и
и 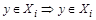 и
и 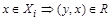 .
.
Покажем, что R транзитивно. Пусть 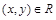 и
и 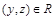 . Тогда найдется множество
. Тогда найдется множество 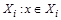 и
и 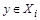 и множество
и множество 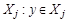 и
и 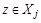 . Но так как различные блоки разбиения не пересекаются, а
. Но так как различные блоки разбиения не пересекаются, а 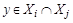 , то
, то 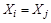 . Следовательно,
. Следовательно, 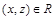 и R транзитивно.
и R транзитивно.
Отношение R обладает свойствами рефлексивности, симметричности, транзитивности, т.е. является отношением эквивалентности. Теорема доказана.
Отношения порядка
Рассмотрим отношения G, L из 1.2.4, отношение Q из 1.2.2 и отношение включения V на множестве всех подмножеств целых чисел (B(Z) – булеан множества Z): 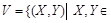 B(Z)
B(Z) 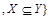 .
.
Таблица 1.4
Свойства отношений
| Отношение | Р | АР | С | АС | НС | Т |
| G | - | + | - | - | + | + |
| L | + | - | - | + | - | + |
| Q | + | - | - | + | - | + |
| V | + | - | - | + | - | + |
Мы видим, что по свойствам эти отношения разделились на два типа.
Определение. Отношение R на множестве Х, обладающее свойствами рефлексивности, антисимметричности, транзитивности, называется отношением порядка на множестве Х (обозначается “p”).
Определение. Отношение R на множестве Х, обладающее свойствами антирефлексивности, несимметричности, транзитивности, называется отношением строгого порядка.
Таким образом, отношения L, Q, V являются отношениями порядка на соответствующих множествах, а отношение G – отношением строгого порядка.
Диаграммы Хассе
Для наглядного представления частично упорядоченного множества 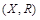 используют диаграмму Хассе – граф отношения R без петель и транзитивно замыкающих дуг.
используют диаграмму Хассе – граф отношения R без петель и транзитивно замыкающих дуг.
Пусть 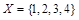 . Рассмотрим на множестве X отношения порядка “ £ ” и “ ½ ”. Получим два частично упорядоченных множества (X, £ ) и (X, ½), различия которых наглядно отражают их диаграммы Хассе (рис.1.9).
. Рассмотрим на множестве X отношения порядка “ £ ” и “ ½ ”. Получим два частично упорядоченных множества (X, £ ) и (X, ½), различия которых наглядно отражают их диаграммы Хассе (рис.1.9).
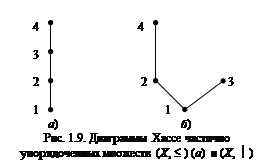 |
Определение. Элемент 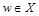 называется наибольшим элементом частично упорядоченного множества
называется наибольшим элементом частично упорядоченного множества 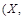 p), если
p), если 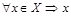 p w. Элемент
p w. Элемент 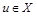 называется максимальным элементом частично упорядоченного множества
называется максимальным элементом частично упорядоченного множества 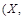 p), если в множестве X нет элемента y такого, что u p y.
p), если в множестве X нет элемента y такого, что u p y.
Элемент 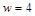 является наибольшим и одновременно максимальным для (X, £ ) (рис. 1.9, а). В частично упорядоченном множестве (X, ½ ) есть два максимальных
является наибольшим и одновременно максимальным для (X, £ ) (рис. 1.9, а). В частично упорядоченном множестве (X, ½ ) есть два максимальных 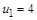 и
и 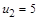 , но нет наибольшего (рис. 1.9, б).
, но нет наибольшего (рис. 1.9, б).
Аналогично определяются понятия наименьшего и минимального элементов частично упорядоченного множества.
Теорема. Всякое частично упорядоченное множество имеет не более одного наибольшего элемента.
Доказательство. Пусть 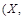 p) – частично упорядоченное множество. Теорема утверждает, что если в множестве
p) – частично упорядоченное множество. Теорема утверждает, что если в множестве 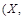 p) имеется наибольший элемент, то он единственный. Предположим противное: пусть имеется два различных наибольших элемента
p) имеется наибольший элемент, то он единственный. Предположим противное: пусть имеется два различных наибольших элемента 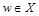 и
и 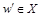 . Тогда по определению наибольшего элемента w p
. Тогда по определению наибольшего элемента w p 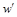 и
и 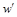 p w, откуда в силу антисимметричности отношения порядка “ p ” следует
p w, откуда в силу антисимметричности отношения порядка “ p ” следует 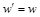 - противоречие, что и доказывает теорему.
- противоречие, что и доказывает теорему.
Реляционная алгебра
Равномощные множества
Напомним, что отображение 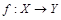 является биекцией (см.1.2.1) тогда и только тогда, когда каждый элемент х множества Х имеет единственный образ
является биекцией (см.1.2.1) тогда и только тогда, когда каждый элемент х множества Х имеет единственный образ 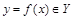 , а каждый элемент
, а каждый элемент 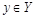 имеет единственный прообраз
имеет единственный прообраз 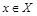 , т.е.
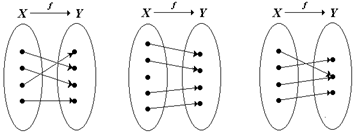
, т.е. 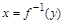 . Так, соответствие между множествами X и Y на рис. 1.20, а является биекцией, а на рис. 1.20, б, в – не является биекцией (объясните почему).
. Так, соответствие между множествами X и Y на рис. 1.20, а является биекцией, а на рис. 1.20, б, в – не является биекцией (объясните почему).
 |
а) б) в)
Рис. 1.20. Соответствие множеств X и Y
а) биективное;
б) в) не биективное
Определение. Будем говорить, что множества X и Yравномощны, если существует биекция множества X на множество Y.
 Пример. Покажем, что множества
Пример. Покажем, что множества 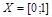 и
и 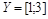 равномощны. Действительно, можно установить биекцию
равномощны. Действительно, можно установить биекцию 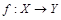 , например, по закону
, например, по закону 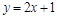 (рис. 1.19, а). Биекцию между множествами X и Y можно установить и геометрически (рис. 1.19, б). Через левые концы отрезков проведена прямая l , через правые – прямая m. Точка пересечения прямых l и m обозначена М. Из точки М проводим лучи, пересекающие оба отрезка; при этом точке пересечения с лучом на первом отрезке соответствует единственная точка пересечения с лучом на втором отрезке (и наоборот).
(рис. 1.19, а). Биекцию между множествами X и Y можно установить и геометрически (рис. 1.19, б). Через левые концы отрезков проведена прямая l , через правые – прямая m. Точка пересечения прямых l и m обозначена М. Из точки М проводим лучи, пересекающие оба отрезка; при этом точке пересечения с лучом на первом отрезке соответствует единственная точка пересечения с лучом на втором отрезке (и наоборот).
Классы равномощных множеств
Введенное в 1.4.1 отношение равномощности является отношением эквивалентности “ º “. В самом деле, оно рефлексивно: для каждого множества Х справедливо 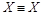 (Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y , то обратное отображение также является биекцией (если
(Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y , то обратное отображение также является биекцией (если 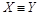 , то
, то 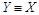 ). Отношение транзитивно: если существует биекция
). Отношение транзитивно: если существует биекция 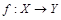 и существует биекция
и существует биекция 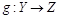 , то соответствие
, то соответствие 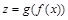 отображает X на Z биективно (если
отображает X на Z биективно (если 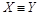 и
и 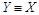 , то
, то 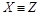 ).
).
По свойству отношения эквивалентности (см. 1.2.5) получаем разбиение всех множеств на непересекающиеся классы равномощных множеств. Каждому классу присвоим название - кардинальное число. Таким образом, кардинальное число – это то общее, что есть у всех равномощных множеств. Обозначим кардинальное число множества 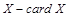 или ½Х½. Пустое множество имеет кардинальное число
или ½Х½. Пустое множество имеет кардинальное число 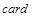 Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества.
Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества.
Свойства конечных множеств
Множество X называется конечным, если существует биекция 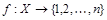 , т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1,2,…,n}; при этом ½X½= n.
, т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1,2,…,n}; при этом ½X½= n.
Все множества, для которых такую биекцию установить невозможно, будем называть бесконечными.
Пустое множество принято относить к конечным множествам и обозначать ½Æ½=0.
Сформулируем свойства конечных множеств в виде теорем (не все теоремы будут строго доказаны).
Теорема (правило суммы). Пусть множество X является объединением r непересекающихся конечных множеств 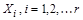 . Тогда
. Тогда 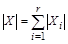 .
.
Согласно условию теоремы система множеств 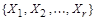 является разбиением множества X. Доказательство проведем методом математической индукции по числу r блоков разбиения.
является разбиением множества X. Доказательство проведем методом математической индукции по числу r блоков разбиения.
Шаг 1. Покажем, что теорема справедлива при 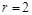 . Пусть
. Пусть 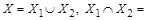 Æи множества
Æи множества 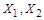 конечны, т.е. существует биекция
конечны, т.е. существует биекция 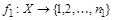 и
и 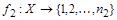 . Установим биекцию
. Установим биекцию 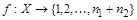 следующим образом: всем элементам множества
следующим образом: всем элементам множества 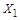 оставим прежние номера, а номера элементов множества
оставим прежние номера, а номера элементов множества 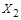 увеличим на число
увеличим на число 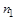 . Полученное отображение
. Полученное отображение
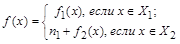
является биекцией 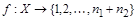 в силу биективности
в силу биективности 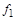 и
и 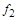 . Следовательно,
. Следовательно, 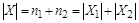 . Основание индукции доказано.
. Основание индукции доказано.
Шаг 2 . Индукционный переход заключается в следующем: предположим, что теорема справедлива при числе блоков разбиения 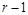 ; докажем, что в этом случае она будет справедлива и при числе блоков r.
; докажем, что в этом случае она будет справедлива и при числе блоков r.
Предположение: множества 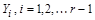 , конечны и образуют разбиение множества Y. Тогда
, конечны и образуют разбиение множества Y. Тогда 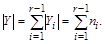
Рассмотрим разбиение множества X на r конечных множеств. Тогда 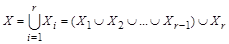 по закону ассоциативности объединения. Обозначим
по закону ассоциативности объединения. Обозначим 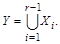 Опираясь на основание индукции (шаг 1), имеем
Опираясь на основание индукции (шаг 1), имеем 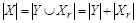 , а по индукционному предположению
, а по индукционному предположению 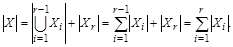 Индукционный переход доказан.
Индукционный переход доказан.
Закл
