РАЗДЕЛ 1 Элементы линейной алгебры

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РБ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ОКТЯБРЬСКИЙ НЕФТЯНОЙ КОЛЛЕДЖ ИМ. С.И. КУВЫКИНА

МАТЕМАТИКА

Методические указания и контрольные задания

для студентов-заочников

по специальностям:

21.02.01 "Разработка и эксплуатация нефтяных и газовых месторождений"

15.02.01"Монтаж и техническое обслуживание промышленного оборудования"

21.02.02"Бурение нефтяных и газовых скважин"

21.02.11“Геофизические методы поисков и разведки месторождения полезных ископаемых”

«ОДОБРЕНО» «УТВЕРЖДАЮ»

Председатель П(Ц)К Заместитель директора

общих математических и естественнонаучных по учебно-методической работе

дисциплин _______________Т.Н. Хайдарова

____________М.Ю.Тинякова «___»_________2014 г.

«___»_________2014 г.

Составитель: З.С. Гибадуллина - преподаватель Октябрьского нефтяного колледжа

Рецензент: М.Ю. Тинякова-преподаватель

Октябрьского нефтяного колледжа

ВВЕДЕНИЕ

Методические указания составлены в соответствии с Федеральным Государственным образовательным стандартом подготовки специалистов среднего звена по специальностям 21.02.01 "Разработка и эксплуатация нефтяных и газовых месторождений", 15.02.01 "Монтаж и техническое обслуживание промышленного оборудования", 21.02.02 "Бурение нефтяных и газовых скважин", 21.02.11 “Геофизические методы поисков и разведки месторождения полезных ископаемых”.

Дисциплина "Математика" относится к циклу "Математические и общие естественно- научные дисциплины" - ЕН.01.

В процессе изучения дисциплины студенты должны усвоить основные понятия, утверждения и методы, изложенные в программе.

Математика и ее методы вторгаются в нашу жизнь, и необходимость их использования ощущается специалистами всех отраслей производства.

Усиленный поток научной информации, математизация наук требует постоянного совершенствования подготовки специалистов с современным математическим образованием. В условиях рыночной экономики специалист среднего звена должен быть организатором производства, руководителем коллектива. Стране нужны специалисты нового типа, высокой квалификации, с широким теоретическим кругозором, способные быстро осваивать новое в науке и технике.

Основная задача дисциплины состоит в том, чтобы дать студентам комплекс математических знаний, умений и навыков, необходимых для изучения смежных и специальных дисциплин, для использования в практической деятельности, для развития логического мышления.

Согласно минимуму содержания программа дисциплины "Математика" состоит из 4 разделов, охватывающих вопросы теоретического и практического характера. К этим разделам относятся элементы линейной алгебры, теории комплексных чисел, основные понятия и методы математического анализа, основы теории вероятностей и математической статистики. В соответствии с требованиями государственного образовательного стандарта СПО в области математики студент должен:

уметь-решать прикладные задачи в области профессиональной деятельности;

знать:

значение математики в профессиональной деятельности и при освоении ППССЗ;

основные математические методы решения прикладных задач в области

профессиональной деятельности;

основные понятия и методы математического анализа, линейной алгебры, теории

комплексных чисел, теории вероятностей и математической статистики;

основы интегрального и дифференциального исчисления.

Итогом изучения дисциплины является сдача экзамена после выполнения контрольной работы.

2. ПРИМЕРНАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН

Наименование разделов и тем		Кол-во ауд. часов
макс. учебн. нагрузка	всего	пр. занятия	Самост. работа
Введение
Раздел 1. Элементы линейной алгебры
1.1 Матрицы и определители 1.2
1.3 Системы линейных уравнений 1.4
Раздел 2 Основы теории комплексных чисел
Раздел 3 Основные понятия и методы математического анализа
3.1 Функции, пределы, непрерывность
3.2 Основы дифференциального исчисления
3.3 Основы интегрального исчисления
Раздел 4 Основы теории вероятностей и математической статистики
4.1 Основные понятия и теоремы теории вероятностей
4.2 Случайные величины
4.3 Основы мат. статистики
Итого

СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ

И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ВВЕДЕНИЕ

Студент должен:

иметь представление:

о роли математики при изучении общепрофессиональных и

специальных дисциплин и в профессиональной деятельности.

История возникновения, развития и становления математики как основополагающей дисциплины, необходимой для изучения профессиональных дисциплин. Цель, задачи математики. Связь математики с общепрофессиональными и специальными дисциплинами.

Методические указания

Изучение данной темы необходимо начинать с определения основных понятий: матрица и определитель. Действия над матрицами сначала надо изучить на матрицах второго порядка, далее переходить на матрицы более высоких порядков. Методы вычисления определителей так же сначала отрабатывают на определителях второго порядка, потом на определителях третьего порядка, только после этого переходят на вычисление определителей высоких порядков. После овладения техниками вычисления определителей и зная действия над матрицами, легко можно научиться находить ранг матрицы, обратную матрицу и решать матричные уравнения.

Вопросы для самоконтроля.

1. Дайте определение матрицы.

2. Какие виды матриц вы знаете?

3. Какие математические действия можно совершать над матрицами?

4. Как выполняется сложение матриц? Свойства сложения матриц.

5. Как выполняется умножение матрица на число?

6. Как выполняется умножение матриц?

7. Что значит транспонировать матрицу?

8. Сформулируйте условие равенства матриц.

9. Как находится определитель второго порядка?

10. Как находится определитель третьего порядка?

11. Какими свойствами обладают определители?

12. Какие методы вычисления определителей вы знаете?

13. Что такое миноры и алгебраические дополнения?

14. Сформулируйте теорему Лапласа.

15. Дайте определение ранга матрицы.

16. Дайте определение обратной матрицы.

17. Сформулируйте алгоритм нахождения обратной матрицы.

18. Сформулируйте алгоритм решения простейших матричных уравнений.

Тема 1.2.

Системы линейных уравнений.

Студент должен:

уметь: - решать системы n линейных уравнений с n переменными различными

способами;

- использовать теорему Кронекера-Капелли для исследования системы

линейных уравнений;

- находить общее и частное решения неоднородной системы линейных

уравнений;

- находить общее решение и фундаментальную систему решений однородной

системы линейных уравнений;

- решать простейшие задачи прикладного характера;

Системы т линейных уравнений с n переменными, совместные и несовместные системы, определенные и неопределенные системы. Системы n линейных уравнений с n переменными. Матричный метод решения систем. Метод Крамера, Метод Гаусса. Исследование систем линейных уравнений. Теорема Кронекера-Капелли. Однородные системы линейных уравнений. Фундаментальная система решений.

Методические указания.

Рекомендуется все способы решения систем сначала отрабатывать на системах 2 уравнений с двумя переменными, потом на системах трех уравнений с тремя переменными. Для решения систем , которые содержат больше пяти уравнений с пятью неизвестными, лучше использовать метод Гаусса.

Вопросы для самоконтроля.

1. Дайте определение системы т линейных уравнений с n переменными.

2. Какие системы называются совместными , несовместными ?

3. Какие системы называются определенными, неопределенными ?

4. Дайте определение системы n линейных уравнений с n переменными.

5. В чем состоит матричный метод решения систем?

6. В чем состоит метод Крамера?

7. Сформулируйте алгоритм решения систем методом Гаусса.

8. Как исследовать системы линейных уравнений?

9. Сформулируйте теорему Кронекера-Капелли.

10. Дайте алгоритм решения однородных систем линейных уравнений.

11. Как найти фундаментальную систему решений.

Раздел 2

Методические указания.

Данную тему рекомендуется начать с определения мнимой единицы и степеней мнимой единицы. Далее необходимо определить комплексное число в алгебраической форме. Изучить арифметические действия над комплексными числами в алгебраической форме. Перед изучением деления вводится понятие комплексно- сопряженного числа. Через геометрическую интерпретацию вводится тригонометрическая форма комплексного числа. Далее необходимо выделить алгоритм перехода от алгебраической формы к тригонометрической форме. В тригонометрической форме изучить умножение, деление, возведение в степень и извлечение корня. Перед введением показательной формы необходимо изучить формулы Эйлера. Отработать технику перехода от тригонометрической формы в показательную форму, показательной формы в тригонометрическую форму и алгебраическую форму. Перед изучением действий в показательной форме нужно повторить действия над степенями.

Вопросы для самоконтроля.

1.Дайте определение мнимой единицы.

2. Сформулируйте алгоритм вычисления степени мнимой единицы.

3. Дайте определение комплексного числа.

4.Что называют действительной (мнимой) частью комплексного числа?

5. Когда комплексные числа равны?

6. Как складываются комплексные числа?

7. Как найти разность комплексных чисел?

8. Как умножаются комплексные числа?

9. Какие числа называются комплексно-сопряженными?

10. Как изобразить комплексное число на координатной плоскости?

11. Что такое аргумент, модуль комплексного числа?

12. Как перейти из алгебраической формы в тригонометрическую форму?

13. Какие действия выполняем над комплексными числами в тригонометрической форме? Каким образом (формулы)?

14. Как записываются формулы Эйлера.

15. Сформулируйте правило перехода из тригонометрической формы в показательную форму.

16. Сформулируйте правило перехода из алгебраической формы в показательную форму и обратно.

17. Сформулируйте правила действия над комплексными числами в показательной форме.

Раздел 3

Основные понятия и методы математического анализа

Методические указания.

При изучении данной темы сначала рассматривают определение функции, ее свойства на примерах элементарных функций, затем уже обобщают понятия. Определение предела функции и его смысла рассматривать лучше графически. Для вычисления пределов и раскрытия неопределенностей используют алгебраические преобразования и эквивалентные функции, а так же два замечательных предела.

Вопросы для самоконтроля.

1. Дайте определение функции.

2. Дайте определение области определения и области значения функции.

3. Как исследовать функцию на четность нечетность?

4. Как найти точки пересечения с координатными осями?

5. Что такое промежутки знакопостоянства и монотонности функции?

6. Дайте определение предела функции.

7. Как находят левый и правый пределы функции?

8. Сформулируйте теоремы о пределах функции и следствия из них.

9. Что такое неопределенность. Какие неопределенности знаете?

10. Дайте определения бесконечно больших и бесконечно малых функции.

11. Какими свойствами они связаны?

12. Какие пределы называют замечательными?

13. Дайте определение непрерывной функции.

14.Как классифицируют точки разрыва функции?

Методические указания

Каждому математическому действию соответствует обратное ему действие. Для дифференцирования существует обратное действие-интегрирование. Нужно разобраться в определении первообразной для функции f(х), понять неоднозначность нахождения первообразной, а затем следует изучить определение неопределенного интеграла, основные свойства неопределенного интеграла.

Зная формулы дифференцирования, студент легко сможет выписать в таблицу основные интегралы. Эти интегралы называются табличными интегралами.

Из способов интегрирования рекомендуется изучить лишь непосредственное интегрирование (приведение к одному или нескольким табличным интегралам) и метод подстановки (замены переменной). В рекомендуемой литературе приводится схема интегрирования методом подстановки и множество решенных примеров на нахождение интегралов по данному методу. Все это позволит студенту понять сущность интегрирования методом подстановки.

После серьезной работы над темой "Неопределенный интеграл" студенту не составит огромного труда изучить такие вопросы как:

- определение определенного интеграла;

- основные свойства определенного интеграла (предлагается пять свойств, среди них два свойства аналогичны свойствам неопределенного интеграла);

- методы вычисления определенного интеграла: непосредственный и метод подстановки.

Определенный интеграл широко применяется для вычисления различных геометрических и физических величин. Следует разобраться в следующих приложениях определенного интеграла:

- вычисление площади плоских фигур (геометрический смысл определенного интеграла);

- нахождение объема тела вращения;

- вычисление пути пройденного точкой и скорости тела;

- вычисление работы силы.

Вопросы для самоконтроля

1. Какая функция называется первообразной для функции f (х) ?

2. Дайте определение неопределенного интеграла.

3. Перечислите основные свойства неопределенного интеграла.

4. Каким действием можно проверить интегрирование ?

5. Напишите основные формулы интегрирования (табличные интегралы).

6. Дайте определение определенного интеграла.

7. Перечислите основные свойства определенного интеграла.

8. В чем заключается геометрический смысл определенного интеграла ?

9. Приведите примеры физических и технических задач, которые можно решить с помощью определенного интеграла.

Раздел 4.

Основы теории вероятностей и математической статистики

Основные понятия и теоремы теории вероятностей.

Студент должен:

знать: понятия: перестановки, размещения, сочетания, события,

частоты и вероятности появления события, совместного и

несовместного события; теоремы сложения вероятностей;

уметь: находить вероятность в простейших задачах, используя

классические определения вероятностей; решать задачи с

применением теоремы сложения вероятностей для

несовместимых событий.

.Основные понятия комбинаторики. Понятие события и вероятности события. Достоверные и невозможные события. Классическое определение вероятностей. Теорема сложения вероятностей. Формула полной вероятности. Формула Байеса. Повторные независимые испытания, формула Бернулли

Методические указания

Прежде чем познакомиться с основными понятиями теории вероятностей следует рассмотреть три типа комбинаций: перестановки, размещения, сочетания. Уяснить для себя, чем отличаются перестановки от размещения, перестановки от сочетания, размещения от сочетания.

По рекомендуемой литературе разобраться в формулах и в решенных комбинаторных задачах. Рассмотрите понятие случайного события и на примерах разберитесь в видах события: невозможные, достоверные, совместные, несовместные, зависимые, независимые.

После этих понятий следует изучить классическое определение вероятности события, и научиться находить вероятность в простейших задачах, используя классическое определение вероятностей.

Из операций над событиями необходимо познакомиться лишь с суммой конечного числа событий.

Изучение теоретического материала следует сопровождать рассмотрением

решенных задач по предложенным учебникам, а затем следует ответить на вопросы для самоконтроля.

Вопросы для самоконтроля

1. Что называется n - факториалом ?

2. Что называется перестановками ? Запишите формулу .

3. Что называется размещениями ? Запишите формулу .

4. Что называется сочетаниями ? Запишите формулу .

5. Что понимается под случайным событием ? Приведите примеры.

6. Какие события называются достоверными ? Приведите примеры.

7. Какие события называются невозможными ? Приведите примеры.

8. Что понимается под вероятностью события ?

9. Дайте классическое определение вероятности события.

10. Какие события называются несовместными, совместными ? Приведите примеры.

11. Как формулируется теорема сложения вероятностей ?

12. Дайте определение частоты наступления события и объясните от чего она зависит ?

13. Какими свойствами обладает вероятность события ?

14. Какие события называются независимыми, зависимыми ? Приведите примеры.

Тема 4.2 Случайные величины

Студент должен:

знать: -способы задания случайной величины;

-определение непрерывной и дискретной случайной величины;

-закон распределения случайной величины;

- определение математического ожидания, дисперсии

дискретной случайной величины;

уметь: -строить ряд распределения случайной величины;

-находить функцию распределения случайной величины.

-находить математическое ожидание и дисперсию случайной

величины по заданному закону ее распределения.

Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины. Биноминальное распределение. Математическое ожидание, дисперсия, среднее квадратичное отклонение. Формулы для вычисления основных числовых характеристик случайных величин..

Методические указания

Случайное событие, связанное с некоторым опытом, является качественной характеристикой опыта. Количественной же характеристикой результата проведенного опыта является случайная величина.

Рассматривая примеры, необходимо усвоить понятие случайной величины, виды случайной величины (дискретной и непрерывной) и их определения. Нужно рассмотреть соответствие между возможными значениями случайной величины и их вероятностями. Такое соответствие называется законом распределения случайной величины. Закон распределения случайной величины удобно задавать в виде таблицы.

Наиболее исчерпывающей характеристикой случайной величины является ее закон распределения вероятностей. Однако не всегда обязательно знать весь закон распределения. Иногда можно обойтись одним или несколькими числами, отражающими наиболее важные особенности закона распределения, например, числом, имеющим смысл "среднего значения" случайной величины, или же числом, показывающим средний размер отклонения случайной величины от своего среднего значения. Такого рода числа называются числовыми характеристиками случайной величины. Оперируя числовыми характеристиками, можно решать многие задачи, не пользуясь законом распределения.

Из числовых характеристик рекомендуется изучить математическое ожидание и дисперсию случайной величины. Наряду с понятиями этих чисел следует разобраться в формулах вычисления математического ожидания и дисперсии случайной величины

Вопросы для самоконтроля

1. Какая величина называется случайной ?

2. Какая случайная величина называется дискретной ?

3. Что называется законом распределения случайной величины ?

4. Как строится ряд распределения дискретной случайной величины ?

5. Какое равенство справедливо для вероятностей случайной величины ?

6. Что называется математическим ожиданием дискретной случайной величины ?

7. Что называется дисперсией случайной величины ?

8. Чему равно математическое ожидание дискретной случайной величины ?

9. Какая формула применяется для вычисления дисперсии случайной величины Х ?

Методические указания.

Цель математической статистики состоит в указании методов сбора и группировки статистических сведений, которые получены в результате экспериментов или наблюдений. Вторая задача- это разработка методов анализа статистических данных: оценки вероятности события, а также функций и параметров распределения; оценка зависимости случайной величины от других случайных величин; проверка статистических гипотез о виде и виде величинах параметров неизвестного распределения.

Вопросы для самоконтроля.

1. Дайте определение генеральной и выборочной совокупности.

2. Укажите способы отбора.

3. Дайте определение статистического распределения выборки и его характеристики

4. Что называют эмпирической функцией распределения?

5. Как строится график эмпирической функции?

6. Что называют полигоном и гистограммой?

7. Какие виды статистических оценок вы знаете?

8. Что такое доверительный интервал?

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Номер темы	Номер и наименование работы	Количество аудиторных часов
1.1 1.2	Вычисление матричного многочлена. Решение систем линейных уравнений методом Крамера.
	Действия над комплексными числами в алгебраической, тригонометрической и показательных формах
3.1 3.2 3.3	Производная сложной функции. Исследование функции и построение графика
4.1 4.2 4.3	Решение простейших задач на определение вероятности. Нахождение математического ожидания и дисперсии случайной величины по заданному закону распределения

ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

ОБЩИЕ ТРЕБОВАНИЯ

Требования к выполнению и оформлению контрольной работы.

1. Работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.

2. На обложке тетради должен быть приклеен титульный лист утвержденного образца и аккуратно записаны все данные: шифр, Ф. И. О. студента, предмет и номер работы.

3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.

4. Решение задачи располагайте в порядке номеров, указанных в задании, номера задач следует указывать перед условием.

5. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь.

6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:

- студенты должны соблюдать абзацы, всякую новую мысль следует начинать с новой строки;

- важные формулы равенства, определения нужно выделять в отдельные строки;

- при описании решения задачи краткая запись условия отделяется от решения и в конце решения ставится ответ;

- серьезное внимание следует уделять правильному написанию сокращенных единиц измерения;

- необходимо правильно употреблять математические символы.

7. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.

8. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.

9. В конце работы следует указать литературу, которой вы пользовались, проставить дату выполнения работы и подпись.

10. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.

Контрольные работы должны быть выполнены в срок (в соответствии с учебным планом - графиком). В период сессии работы на проверку не принимаются. Если в работе допущены недочеты и ошибки, то студент должен выполнить все указания преподавателя, сделанные в рецензии.

Студенты, не имеющие зачет по контрольной работе, к экзамену не допускаются. Во время экзамена зачтенные контрольные работы предоставляются преподавателю.

Контрольная работа имеет 30 вариантов. Вариант работы выбирается согласно двум последним цифрам шифра студента.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

К решению первой задачи контрольной работы следует приступить после изучения темы «Матрицы и определители».

Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов:

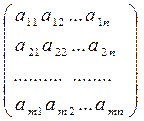
Сокращенно можно записать 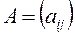, где

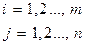
Любой элемент -это элемент, находящейся на пересечении 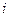-той строки и 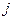-того столбца.

Если количество строк n не равно количеству столбцов m, то матрицу называют прямоугольной.

Пример.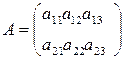

Если количество строк n равно количеству столбцов m, то матрицу называют квадратной.

Пример. .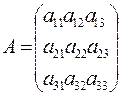

Число строк и столбцов квадратной матрицы называют порядком квадратной матрицы.

Рассмотрим квадратную матрицу порядка n: 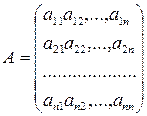.Диагональ, содержащая элементы 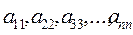- главная диагональ, диагональ содержащая 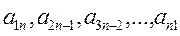-побочная диагональ.

Матрица вида 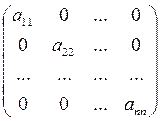называется диагональной.

Пример. .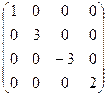

Если у диагональной матрицы все числа равны, то есть 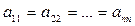, то матрица называется скалярной. Скалярную матрицу, у которой все числа главной диагонали равны единице, называют единичной и обозначают E.

Пример. .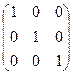

Матрицу, у которой все элементы равны 0, называют нулевой матрицей и обозначают 0=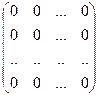

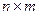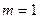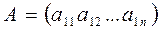В прямоугольной матрице типа , если , то - матрица- строка.

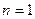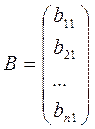Если , то -матрица- столбец

Матрицы-строки и матрицы-столбцы иначе называются векторами.

Две матрицы называются равными, если у них одинаковое число строк m и одинаковое число столбцов n и их соответствующие элементы равны: .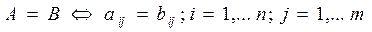

Пример: .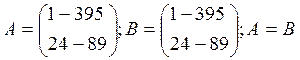

Пусть дана матрица размерности 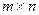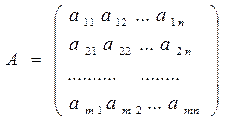.Переставляя строки со столбцами, получаем матрицу размерности 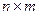, которую называют транспонированной и обозначают .

.

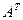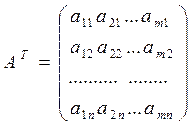Операции над матрицами.

1. Сложение (вычитание) матриц одинаковых размерностей.

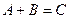. Чтобы найти сумму (разность) двух (и более) матриц с одинаковым числом строк и столбцов необходимо сложить (вычесть) соответствующие элементы.

Пример. ; .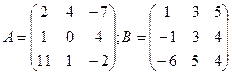

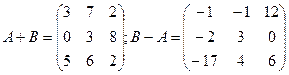Так как сложение матриц сводится к сложению чисел, то данная операция обладает теми же свойствами, что и сложение чисел, а именно:

1. .

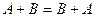2.

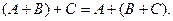
3.

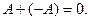
2. Умножение матрицы на число 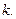Каждый элемент матрицы умножаем на число

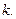
Пример. .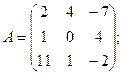

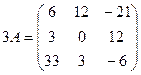Свойства:1.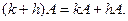

2. .

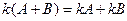3.

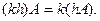
3. Умножение матриц. Матрицы можно перемножить тогда, когда число столбцов матрицы равно числу строк матрицы 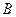. Чтобы найти элемент стоящий на 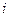-той строке и 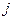-том столбце матрицы 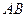, нужно умножить соответствующие элементы 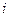строки и 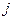столбца и сложить произведения.

Пример.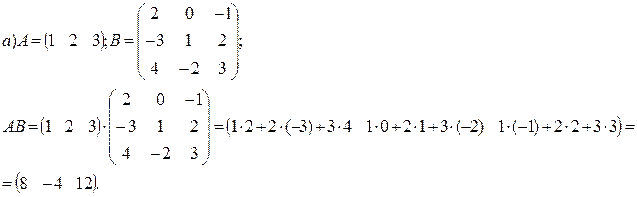

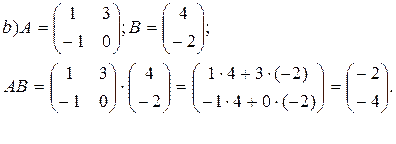
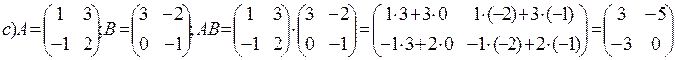
Свойства:

1. .

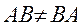2. .

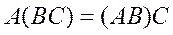3. .

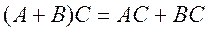Для квадратичных матриц возможно составление многочленов. Многочлен степени 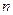от квадратичной матрицы называется выражение

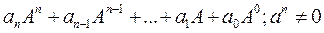или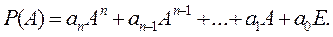

Если 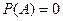, то матрица называется корнем многочлена 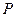, сам многочлен называется аккумулирующим для матрицы .

Пример. Найти значение матричного многочлена ( ):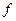

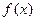=-x³+3x²+x-2, = .

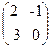Решение. В многочлен 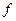вместо 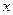подставляем матрицу и в ответе получаем матрицу той же размерности, что и матрица .

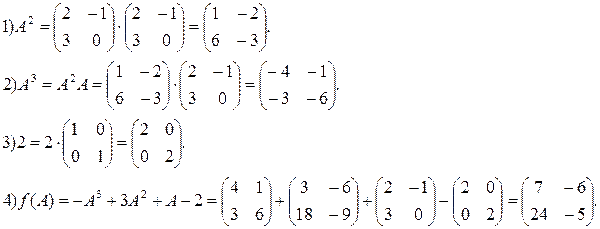
Пусть дана квадратная матрица второго порядка.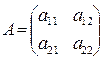

Определителем (детерминантом) второго порядка, соответствующей данной матрице, называется число равное разности произведений элементов главной и побочной диагонали. Обозначение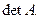

.

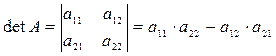Пример. Вычислить .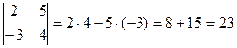

Рассмотрим квадратную матрицу третьего порядка .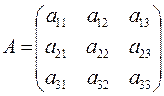

Определитель (детерминант) третьего порядка вычисляется по формуле:

.

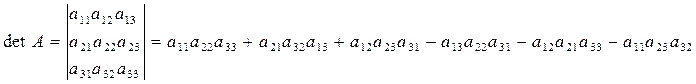Пример. Вычислить

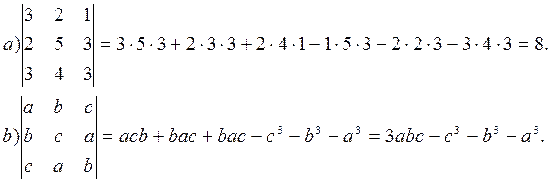
Свойства определителей.

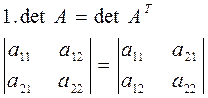
2. При перестановке двух строк или столбцов определитель изменить свой знак на противоположный.

3. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.

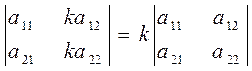
4. Определитель с двумя одинаковыми строками или столбцами равен нулю. Пример. .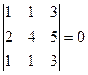

5. Определитель, у которого все элементы двух строк или двух столбцов пропорциональны, равен нулю. Пример.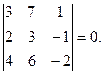

6. Если к какой-либо строке или столбцу определителя прибавить элементы другой строки или столбца, умноженные на одно и то же число, то определитель не изменит своей величины.

.

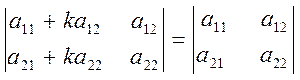7. Треугольный определитель, у которого все элементы лежащие выше или ниже главной диагонали- нули, равен произведению элементов главной диагонали.

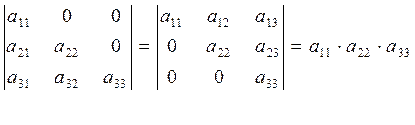
Свойства 6 и 7 дают еще один способ вычисления определителей: приводим определитель к треугольному виду, пользуясь свойством 6 ,и вычисляем его значение, опираясь на свойство 7.

Пример.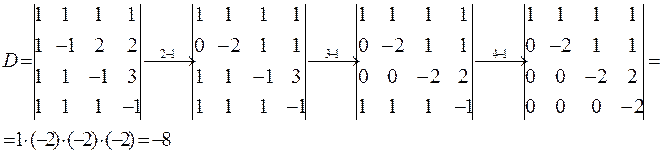

Рассмотрим определитель .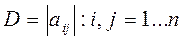

Минором 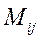элемента 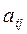определителя 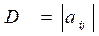называется новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.

Пример. 1)Минор элемента 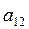будет .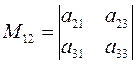

2)Выпишем все миноры определителя третьего порядка .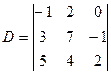

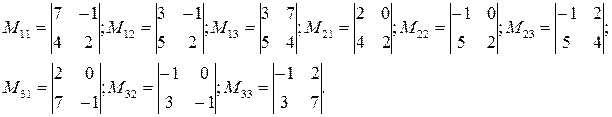
Алгебраическим дополнением элемента 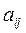определителя 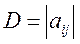называется минор 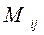этого элемента, взятый со знаком 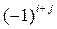, и обозначается . .

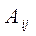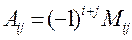Пример.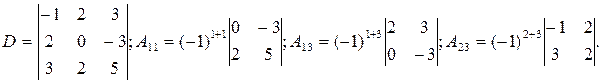

Сумма произведений элементов любой строки или столбца определителя 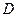на их алгебраические дополнения равна этому определителю.

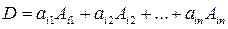- разложение определителя по элементам 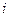-той строки. 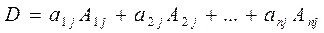- разложение определителя по элементам 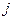-того столбца.

Пример. 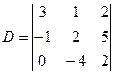. Найдем значение это