Векторы. ортогоанльные и коллинеарные векторы. сложение векторов, умножение на число, скалярное произведение
Вопросы
1. Какая величина называется скалярной.
2. Какая величина называется векторной. Что такое геометрический вектор.
3. Что называется модулем вектора.
4. Какой геометрический вектор называется нулевым (его длина и направление).
5. Когда равны два геометрических вектора.
6. Что такое свободный вектор.
7. Как найти сумму нескольких геометрических векторов.
8. Как сложить два вектора по правилу параллелограмма.
9. Как сложить три вектора по правилу параллелепипеда.
10. Свойства векторного сложения.
11. Как определяется вектор 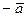 , противоположный к вектору
, противоположный к вектору 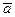 .
.
12. Как найти разность векторов 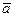 и
и 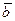 .
.
13. Как определяется вектор 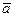 , умноженный на скаляр k..
, умноженный на скаляр k..
14. Свойства умножения вектора на скаляр.
15. Какой вектор называется ортом (направляющим вектором) вектора 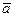 (его длина и направление).
(его длина и направление).
16. Какие два вектора называются коллинеарными. Основное свойство коллинеарных векторов.
17. Что называется осью.
18. Определение составляющей вектора 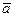 относительно оси l.
относительно оси l.
19. Какое число называется проекцией вектора 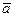 на ось l.
на ось l.
20. Основные свойства проекции вектора на ось.
21. Что такое прямоугольная декартова система координат.
22. Что такое радиус-вектор точки пространства.
23. Что называется координатами точки М в 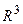 (как это понятие связано с радиус-вектором точки М).
(как это понятие связано с радиус-вектором точки М).
24. Что такое единичный вектор (орт) оси.
25. Теорема о разложении произвольного вектора 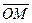 по ортам координатных осей.
по ортам координатных осей.
26. Как найти длину (модуль) вектора в 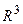 .
.
27. Как найти координаты вектора, зная координаты его начала и конца.
28. Как найти расстояние между точками 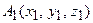 и
и 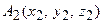 в
в 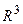 .
.
29. Что называется скалярным произведением векторов в 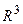 .
.
30. Свойства скалярного произведения.
31. Какие векторы называются ортогональными.
32. Чему равно скалярное произведение ортогональных векторов.
33. Как выглядит условие коллинеарности векторов в координатной форме.
Задачи
48. По данным векторам 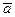 и
и 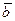 (см. рис.1) построить:
(см. рис.1) построить:
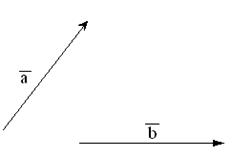
Рис. 1
а) 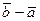 ; б)
; б) 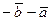 ; в)
; в) 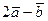 ; г)
; г) 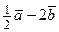 ; д)
; д) 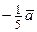 .
.
49. Найти сумму векторов 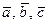 или
или 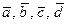 .
.
а) 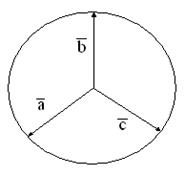 б)
б) 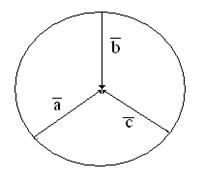
в) 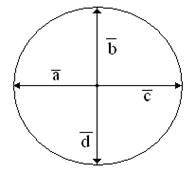 г)
г) 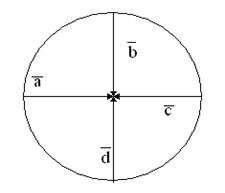 д)
д) 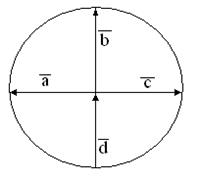 Рис. 2
Рис. 2
50. Для векторов, изображенных на рисунке, найти сумму.
а) б)
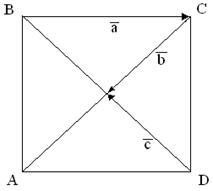
в) г)
Рис. 3
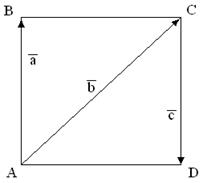
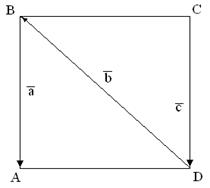
10. Для векторов, изображенных на рис. 3, найти линейную комбинацию:
а) 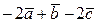 , для рис а);
, для рис а);
б) 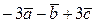 , для рис. б);
, для рис. б);
в) 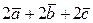 ,
, 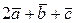 для рис. в)
для рис. в)
г) 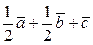 ,
, 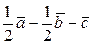 для рис. г)
для рис. г)
52. Пусть 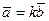 . Причем
. Причем 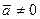 .
.
При каких значениях k будут выполняться равенства:
а) 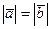 ; б)
; б) 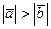 ; в)
; в) 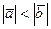 .
.
53. Определить значения k, при которых длина вектора 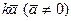 :
:
а) равна длине 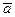 ;
;
б) больше длины 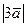 ;
;
в) меньше длины 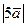 .
.
54. В прямоугольной декартовой системе координат даны точки
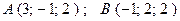 .
.
Найти координаты векторов 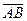 и
и 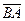 и их длины;
и их длины;
координаты орта 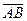 и орта
и орта 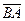 .
.
55. Найти расстояние между точками А и В.
а) 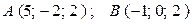
б) 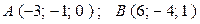
в) 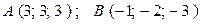
г) 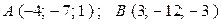
56. Найти координаты точки С, середины отрезка АВ.
а) 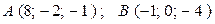
б) 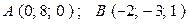
в) 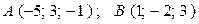
г) 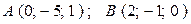
57. Угол между векторами 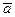 и
и 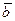 равен
равен 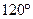 . Зная, что
. Зная, что 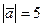 , а
, а 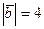 , вычислить:
, вычислить:
а) 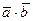 ; б)
; б) 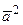 ; в)
; в) 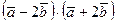 ; г)
; г) 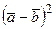 ; д)
; д) 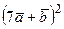 ; е)
; е) 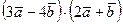 .
.
58. Вычислите:
а) 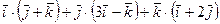 ;
;
б) 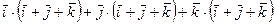 .
.
59. Даны векторы:
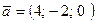 ,
, 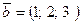 .
.
Вычислить:
а) 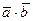 ; б)
; б) 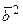 ; в)
; в) 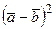 ; г)
; г) 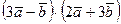 .
.
60. Дан вектор 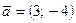 . Известно, что абсцисса ортогонального ему вектора
. Известно, что абсцисса ортогонального ему вектора 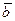 равна 8. Определить ординату.
равна 8. Определить ординату.
61. Найти значение 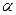 , при котором следующие векторы ортогональны:
, при котором следующие векторы ортогональны:
а) 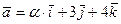 и
и 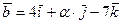 ;
;
б)  и
и 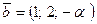 ;
;
в) 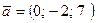 и
и 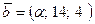 .
.
62. Дан вектор 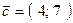 . Найти координаты какого-либо вектора, ортогонального
. Найти координаты какого-либо вектора, ортогонального 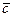 . Сколько решений имеет задача.
. Сколько решений имеет задача.
63. Дан вектор 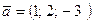 . Известно, что абсцисса ортогонального ему вектора
. Известно, что абсцисса ортогонального ему вектора 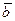 равна 3, а ордината равна – 6. Найти его аппликату.
равна 3, а ордината равна – 6. Найти его аппликату.
64. Дан вектор 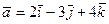 . Найти вектор
. Найти вектор 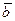 , если
, если 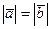 , абсцисса
, абсцисса 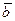 равна ординате
равна ординате 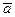 , ордината
, ордината 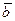 равна нулю.
равна нулю.
65. Даны два вектора: 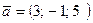 и
и 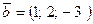 .
.
Найти вектор  , ортогональный оси OZ и удовлетворяющий условию:
, ортогональный оси OZ и удовлетворяющий условию:
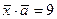 и
и 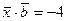 .
.
66. Найти значение 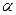 , при котором следующие векторы коллинеарны:
, при котором следующие векторы коллинеарны:
а) 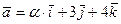 и
и 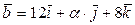 ;
;
б) 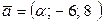 и
и 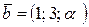 ;
;
в) 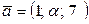 и
и 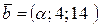 .
.
67. Найти вектор 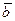 , коллинеарный вектору
, коллинеарный вектору 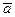 и удовлетворяющий условию;
и удовлетворяющий условию;
а) 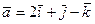 ;
; 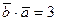 ;
;
б) 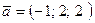 ;
; 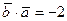 .
.
68. Найти вектор 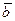 , длина которого равна 50, коллинеарный вектору
, длина которого равна 50, коллинеарный вектору 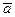 и образующий острый угол с заданной осью:
и образующий острый угол с заданной осью:
а) 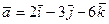 , с осью OX;
, с осью OX;
б) 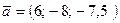 , с осью OZ.
, с осью OZ.
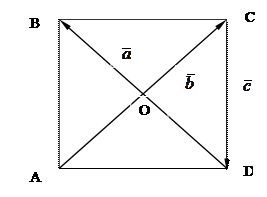
69. В прямоугольной системе координат ABCD проведены диагонали параллелограмма 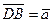 и
и 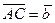 (см. рис.4).
(см. рис.4).
Представьте векторы 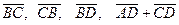 в виде линейной комбинации векторов
в виде линейной комбинации векторов 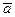 и
и 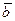 .
.
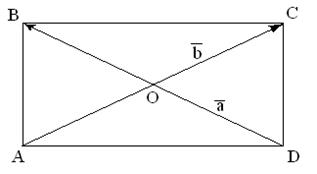
Рис. 4
70. В параллелограмме ABCD 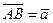 ,
, 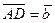 . Точка О – точка пересечения диагоналей (см. рис. 5).
. Точка О – точка пересечения диагоналей (см. рис. 5).
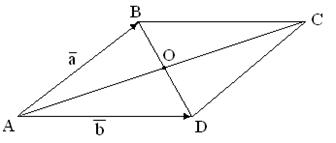
Рис. 5
Разложите векторы 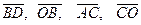 по векторам
по векторам 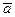 и
и 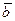 .
.
СЕМИНАР 10.
