N-мерные векторы. операции над ними.

СВОЙСТВА ОПЕРАЦИЙ НАД ВЕКТОРАМИ

Вопросы

1. Закон коммутативности сложения.

2. Закон коммутативности умножения.

3. Закон ассоциативности сложения.

4. Закон ассоциативности умножения.

5. Закон дистрибутивности.

6. Определение n-мерного вектора, его координат.

7. Размерность вектора.

8. Когда два вектора равны?

9. Нулевой вектор.

10. Свойства суммы n-мерных векторов.

11. Свойства суммы n-мерных векторов.

12. Произведение n-мерного вектора на число k.

13. Свойства произведения n-мерного вектора на число k.

14. Длина n-мерного вектора.

15. Скалярное произведение векторов.

16. Свойства скалярного произведения n-мерных векторов.

17. Косинус угла между двумя n-мерными векторами.

18. Формула для скалярного произведения векторов через косинус угла между ними.

Задачи

11. Даны точки в пространстве R 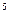. Найти расстояния 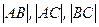с точностью до 0,0001.

а) А (1, 0, 1, 0, 2), В (1, –2, 1, – 1, 0), С (1, 2, 0, 1, –1);

б) А (0, 0, 1, 3, –2), В (1, 1, 1, – 2, 0), С (0, 2, –1, –1, 1);

12. Найти вектор 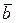, выраженный линейной комбинацией векторов , , и , если , , , :

а) ,

б) .

13. Найти линейную комбинацию векторов:

а) ,

б) ,

где .

14. Дана система векторов , ,

Решить уравнение:

а)

б)

15. Найти вектор 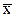из уравнения:

а) ,

где

б)

где

16. Для системы векторов найти: длины векторов ;

скалярные произведения векторов ; углы между векторами: ; значение выражения: .

а) б) в)

МАТРИЦЫ. ОПРЕРАЦИИ НАД НИМИ

Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. Числа этой таблицы называются элементами матрицы и обозначаются .

.

Элементы составляют i - ю строку (i = 1, 2, …, m) матрицы, элементы – ее j-ый столбец (k = 1, 2, . . . , n).

Матрица, состоящая из одной строки, называется матрицей-строкой. Матрица, имеющая один столбец, называется матрицей-столбцом.

Квадратной называется матрица, у которой число строк равно числу столбцов (m = n).

Порядком квадратной матрицы называется число ее строк (или столбцов).

Элементы квадратной матрицы образуют ее главную диагональ, а элементы – побочную диагональ.

Диагональной называется матрица, все элементы, не стоящие на главной диагонали, равны нулю.

Единичной называется матрица, у которой все элементы главной диагонали равны 1, а остальные 0. Для единичной матрицы характерно то, что .

Если в матрице А все строки заменить столбцами, то полученная матрица называется транспонированной и обозначается .

Операции над матрицами

Суммой матриц и называется такая матрица , элементами которой являются числа, определяемые по формуле

Таким образом, элементы матрицы С равны суммам соответствующих элементов матриц А и В. Сумма матриц A и B обозначается A + B.

Разностью матриц и называется матрица = А - В, для которой

Произведением матрицы на число k называется матрица, полученная из матрицы А умножением всех ее элементов на число k.

Произведение матриц определяется для квадратных матриц одного и того же порядка, а также для неквадратных матриц, у которых число столбцов матрицы-множимого равно числу строк матрицы‑множителя.

Произведением матрицы на матрицу называется такая матрица , для которой

,

т. е. элемент матрицы С представляет собой скалярное произведение i-ой строки матрицы А на k-ый столбец матрицы В (равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В). Матрица С имеет m строк и l столбцов. Произведение матрицы А на матрицу В обозначается АВ.

Замечание. . Если АВ = ВА, то матрицы называются перестановочными.

Пример:

Даны 2 матрицы: .

Найти матрицу С = 2А + АВ.

В соответствии с определениями суммы, произведения матриц и умножения матрицы на число получаем:

.

СЕМИНАР 3.