Некоторые свойства промежутков времени

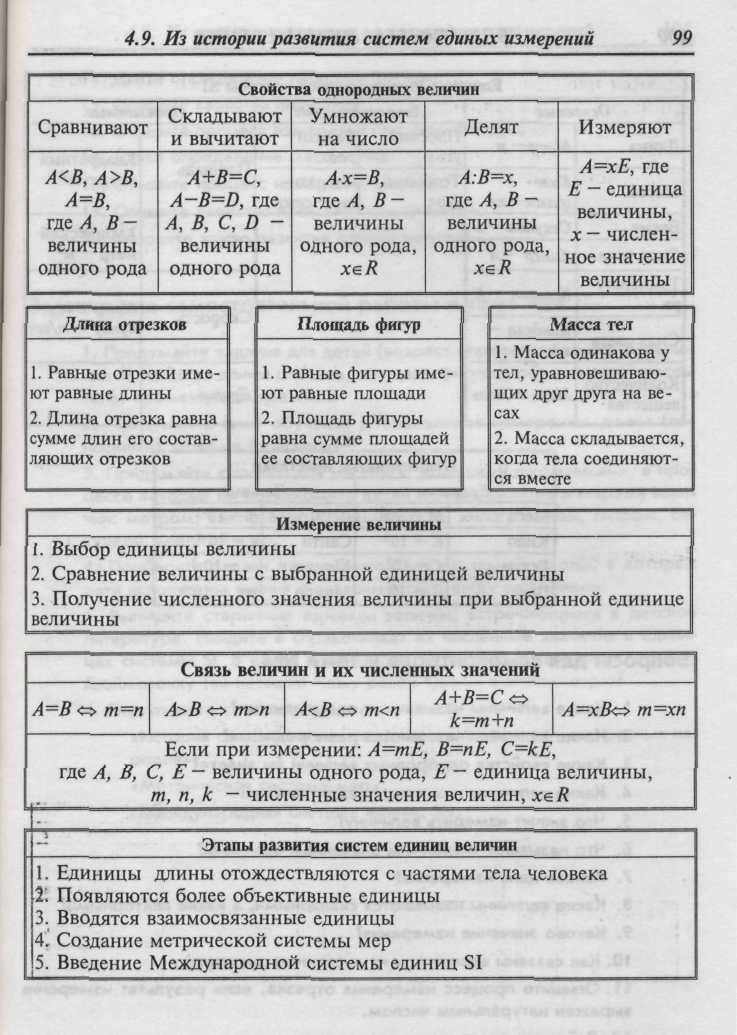
1. Промежутки времени можно сравнивать, («Красная Шапочка затратила больше времени на дорогу до бабушки, чем Серый Волк».)

2. Промежутки времени можно складывать и вычитать. («Маша один час вырезала фигуры и один час их наклеивала. Сколько всего времени она затратила на работу?»)

3. Промежутки времени можно умножать на число. («7 суток — это неделя. Сколько суток в трех неделях?»)

4. Промежутки времени можно измерять.

Процесс измерения времени особенный, его нельзя измерить откладыванием одной и той же мерки, как, например, длину. Поэ­тому в качестве единицы времени выбирается регулярно повторяю­щийся процесс. Такие единицы времени, как год, сутки, были вы­браны на основе природных явлений: смены дня и ночи, смены времен года, а час, минута, секунда придуманы человеком.

Дошкольники знакомятся с понятиями: части суток, дни неде­ли, месяцы и др. Для развития «чувства времени» можно научить их работать с песочными часами, секундомером, определять время по механическим часам.

Младшие школьники знакомятся с общепринятыми единицами времени (секундой, минутой, часом), используют свои знания при решении задач.

Задание 58

Решите задачи.

1. Знаменитый греческий математик Архимед умер в 212 году да

н.э. Сколько веков и сколько лет прошло с тех пор!

Зависимостимежду величинами

Задание 59

Вспомните другие формулы, раскрывающие связи между различ­ными величинами. Назовите единицы этих величин.

Зависимости между величинами разнообразны и изучаются в различных науках: математике, физике, астрономии, химии, эконо­мике, биологии, социологии и др.

Дети рано встречаются с зависимостями между величинами. Например, в рассуждениях:

— чем длиннее путь, тем больше времени необходимо за­тратить (при постоянной скорости);

— чем больше цена, тем больше стоимость товара (при посто­янном количестве);

— у квадрата с большей площадью сторона длиннее.

Эти связи используются дошкольниками в рассуждениях и по­могают им правильно делать выводы. В начальной школе на уроках математики при решении задач также раскрываются зависимости между величинами сначала при помощи рассуждений, а после зна­комства с буквенными выражениями и при помощи формул.

Из истории развития систем единых измерений

Примечание.

Лекция начинается с сообщений на темы: «История создания и развития систем единых измерений разных народов», «Метрическая система мер», «Международная система единиц 57», предварительно подготовленные студентами.

В истории развития систем единых измерений можно выделить несколько периодов. Переход от одного этапа к другому, как прави­ло, обусловливается противоречиями и неудобствами прежних еди­ниц.

Этапы развития единиц величин

I этап.

Единицы длины отождествляются с частями тела человека:

ладонь — ширина четырех пальцев; локоть — длина руки от кисти до локтя; фут - длина ступни;

дюйм - длина сустава большого пальца и др. В качестве единиц площади использовались такие единицы: колодец - площадь, которую можно полить из одного колодца; соха или плуг — средняя площадь, обработанная за день сохой или плугом.

Недостаток таких единиц — нестабильность, необъективность.

II этап.

В XIV-XVI вв. с развитием торговли появляются более объективные единицы. Например:

дюйм - длина трех приставленных друг к другу ячменных зерен;

фут — ширина 64 ячменных зерен, положенных бок о бок;

карат - масса семени одного из видов бобов.

Недостаток — отсутствие взаимосвязи между единицами изме­рений.

III этап.

Введение единиц, взаимосвязанных друг с другом. Например, в России единицы длины были связаны таким образом:

3 аршина — сажень;

500 саженей - верста;

7 верст - миля.

Недостаток - различие единиц в разных странах, что тормозило взаимоотношения между ними, например торговлю.

IV этап.

Создание новой системы единиц во Франции в конце XVIII в. Основная единица длины - метр — одна сорокамиллионная часть

длины земного меридиана, проходящего через Париж. Метр — в переволе с греческого (metron) — мера. Все остальные величины были связаны с метром, поэтому новая система величин получила название метрической системы мер. В ней использовались такие единицы:

ар — площадь квадрата со стороной 10 м;

литр - объем куба с длиной ребра 0,1 м;

грамм — масса чистой воды, занимающей объем куба с длиной ребра 0,01 м.

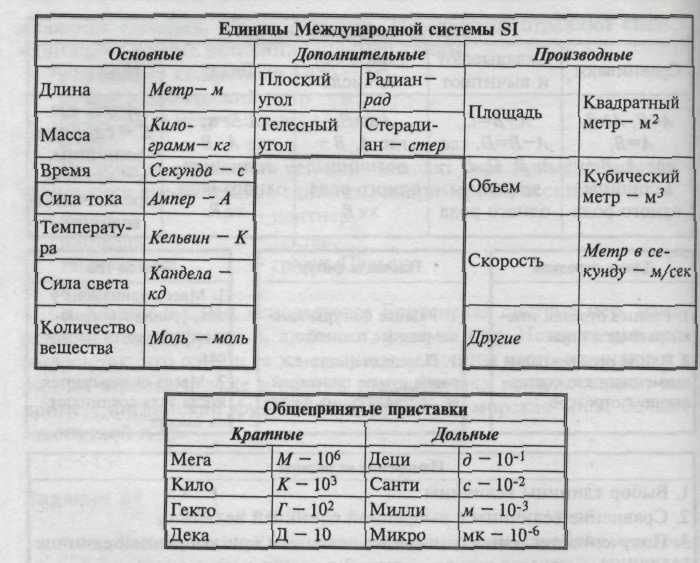
Были введены десятичные кратные и дольные единицы с по­мощью приставок (рис. 87):

Эталоны метра и килограмма, изготовленные из платино-ири-диевого сплава, до сих пор хранятся в Международном бюро мер и весов в Севре, около Парижа. Подобные образцы были переданы другим странам.

Недостаток — с развитием науки потребовались новые единицы и более точное измерение.

V этап.

В I960 г. XI Генеральная конференция мер и весов приняла решение

0 введении Международной системы единиц SI (русск. СИ).

SI — система интернациональная.

В этой системе 7 основных единиц (метр, килограмм, секунда, ампер, кельвин, моль, кандела) и 2 дополнительные (радиан, стера­диан). Эти единицы, определенные в курсе физики, не изменяются в любых условиях.

Задание 60

Назовите единицы основных величин системы SI.

Величины, которые определяются через основные, называются производными величинами. Например, производными величинами

1 - 7975

являются площадь, объем, скорость. Их единицы отражают связь с единицами других величин, например длины:

площадь — квадратный метр — м1,

объем - кубический метр - м3,

скорость — метр в секунду — м/с

и др.

Во многих странах по сей день находят свое применение и ис­пользуются внесистемные единицы, например, в России:

масса — центнер,

площадь — гектар,

температура — градус Цельсия

и др.

В Англии и США используется Британская система мер, изме­рение проводят фунтами, дюймами, футами и др. Исторически сло­жилось так, что одни и те же единицы величины часто отличаются в разных странах и даже в разных направлениях использования, на­пример: английский фунт больше русского, морская миля больше сухопутной и др.

Задание 61

Назовите известные вам внесистемные единицы величин, которы­ми до сих пор пользуются в России и других странах.

Вопросы для самоконтроля к теме №4

1. Какие величины называются однородными?

2. Какие величины называются разнородными?

3. Какие свойства однородных величин вы знаете?

4. Какие величины называются аддитивными?

5. Что значит измерить величину?

6. Что называют численным значением величины?

7. Какова цель измерения?

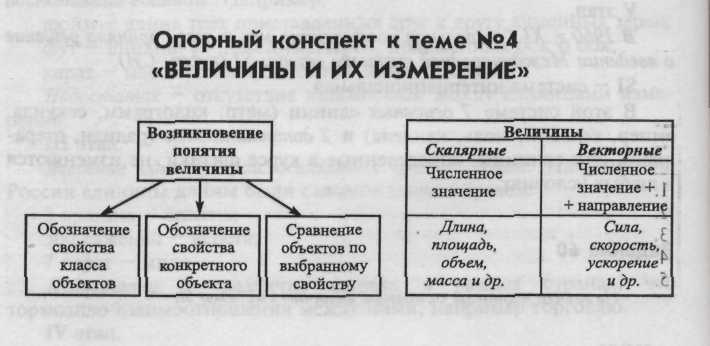
8. Какие величины называются скалярными, а какие векторными?

9. Каково значение измерения?

10. Как связаны величины и их численные значения?

11. Опишите процесс измерения отрезка, если результат измерения выражен натуральным числом.

12. Дайте определение длины отрезка.

13. Опишите свойства длин отрезков.

14. Дайте определение площади фигуры.

15.Опишите свойства площадей.

16. Опишите процесс измерения площади фигуры.

17. Дайте определение массы тепа.

18. Опишите процесс измерения массы.

19. Опишите свойства промежутков времени.

20. Назовите этапы развития единиц величин.

Задания для самостоятельной работы к теме №4

1. Придумайте задания для детей (возраст определите сами), отража­ющие свойства длины отрезка, площади фигуры, объема тела, массы тела, промежутков времени.

2. Придумайте план обучения дошкольников измерению длины (по­лосками), объема (стаканами).

3.Придумайте сюжеты для работы с младшими школьниками, в про­цессе которых вы познакомите детей с общепринятыми мерами вели­чин: метром, сантиметром, дециметром, килограммом, литром, се­кундой, минутой и др.

4.Подберите задачи из учебников для начальной школы, в которых дети используют знания о зависимостях между величинами.

5.Выпишите старинные единицы величин, встречающиеся в детской литературе. Найдите в справочниках их численные значения в едини­цах системы SI. В каких странах они зародились? Например, почему Дюймовочку так назвали? Чему равен 1дюйм в миллиметрах?

6. Подготовьте сообщения на темы:

«История создания и развития систем единиц величин разных на­родов в;

«Метрическая система мер»; «Международная система единиц SI».

ТЕМА 5

НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

«Мы должны склониться перед гением

Человека, создавшего (не открывшего, а

именно создавшего) понятие единицы.

Возник­ло Число, а вместе с ним возникла

Матема­тика. Идея Числа — вот с чего начиналась

история величайшей из наук». Н.Н. Лузин (1883-1950) - крупнейший

рос­сийский математик