Рабочая программа составлена в соответствии с
02.04
Муниципальное бюджетное общеобразовательное учреждение
«Золотухинская средняя общеобразовательная школа»
Золотухинского района Курской области
| Рассмотрена на заседании педагогического совета протокол № __ от « ___» _________ 2017 г. | Утверждена приказом № __ от «__» ______ 2017 г. Директор школы ________________ В.В. Перьков |
РАБОЧАЯ ПРОГРАММА
по учебному предмету «Математика
(алгебра и начала математического анализа)»
для 11 А класса
среднее общее образование
базовый уровень
2017 - 2018 учебный год
Составлена учителем
высшей квалификационной категории
Семенихиной Л. М.
2017 г.
СТРУКТУРА РАБОЧЕЙ ПРОГРАММЫ
1.Пояснительная записка.
2.Содержание программы.
3.Учебно-тематический план.
4.График контрольных работ.
5.Календарно-тематический план.
6.Ресурсное обеспечение программы.
7.Лист корректировки рабочей программы
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
В результате изучения математики на базовом уровне ученик должен
Знать/понимать
· значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
· значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
· универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
· вероятностный характер различных процессов окружающего мира;
Алгебра
Уметь
· выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
· проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
· вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
· практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
Уметь
· определять значение функции по значению аргумента при различных способах задания функции;
· строить графики изученных функций;
· описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
· решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
· описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
Уметь
· вычислять производные и первообразные элементарных функций, используя справочные материалы;
· исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
· вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства
Уметь
· решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
· составлять уравнения и неравенства по условию задачи;
· использовать для приближенного решения уравнений и неравенств графический метод;
· изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
· построения и исследования простейших математических моделей;
Уметь
· решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
· вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизнидля:
· анализа реальных числовых данных, представленных в виде диаграмм, графиков;
· анализа информации статистического характера.
Критерии оценки знаний
Оценка устного ответа
Исходя из поставленной цели и возрастных возможностей учащихся, необходимо учитывать:
1. правильность и осознанность изложения содержания, полноту раскрытия понятий, точность употребления научных терминов;
2. степень сформированности интеллектуальных и обще учебных умений;
3. самостоятельность ответа;
4. речевую грамотность и логическую последовательность ответа.
Оценка “5”:
· полно раскрыто содержание материала в объеме программы и учебника;
· четко и правильно даны определения и раскрыто содержание понятий;
· верно, использованы научные термины;
· для доказательства использованы различные умения;
· ответ самостоятельный, использованы ранее приобретенные знания.
Оценка “4”:
· раскрыто основное содержание материала;
· в основном правильно даны определения понятий и использованы научные термины;
· ответ самостоятельный;
· определения понятий неполные, допущены незначительные нарушения последовательности изложения, небольшие неточности при использовании научных терминов или в выводах и обобщениях.
Оценка “3”:
· усвоено основное содержание учебного материала, но изложено фрагментарно, не всегда последовательно;
· определения понятий недостаточно четкие;
· не использованы в качестве доказательства выводы и обобщения из наблюдений и опытов или допущены ошибки при их изложении;
· допущены ошибки и неточности в использовании научной терминологии, определении понятий.
Оценка “2”:
· основное содержание учебного материала не раскрыто;
· не даны ответы на вспомогательные вопросы учителя;
· допущены грубые ошибки в определении понятий, при использовании терминологии.
Оценка самостоятельных, письменных и контрольных работ.
Оценка “5”
Ставится за работу, выполненную без ошибок и недочетов или имеющую не более одного недочета
Оценка “4”
Ставится за работу, выполненную полностью, но при наличии в ней: не более одной негрубой ошибки и одного недочета, или не более двух недочетов.
Оценка “3”
Ставится в том случае, если ученик правильно выполнил не менее половины работы или допустил:
не более двух грубых ошибок, или не более одной грубой ошибки и одного недочета, или не более одной грубой и одной негрубой ошибки и одного недочета, или не более двух-трех негрубых ошибок, или одной негрубой ошибки и трёх недочетов, или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка “2”
Ставится, когда число ошибок и недочетов превышает норму, при которой может быть поставлена оценка “3”, или если правильно выполнено менее половины работы.
Учитель имеет право поставить оценку выше той, которая предусмотрена “Нормами”, если учеником оригинально выполнена работа.
Оценка тестов.
В качестве нижней границы успешности выполнения основного теста, соответствующего оценке “3” (“зачет”), можно принять уровень - 50% -62% правильных ответов из общего количества вопросов.
Оценка “4” (“хорошо”) может быть поставлена за - 62% - 75%правильных ответов.
Оценка “5” (“отлично”) учащийся должен успешно выполнить тест, более 75%правильных ответов.
Ошибки и недочеты.
Грубыми считаются следующие ошибки:
1. незнание определения основных понятий, законов, правил, незнание формул, общепринятых символов обозначений и единиц их измерения;
2. неумение выделить в ответе главное;
3. неумение применить в ответе знания для решения задач;
4. неумение делать выводы и обобщения;
5. неумение читать и строить графики и диаграммы;
6. неумение пользоваться учебником и справочниками по математике;
7. нарушение техники безопасности при работе в тетради и на доске.
К негрубым ошибкам относятся:
1. неточность формулировок, определений, понятий, законов, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного-двух из этих признаков второстепенными;
2. ошибки, вызванные несоблюдением, условий работы (не точно определена точка отсчета);
3. ошибки в условных обозначениях, неточность графика;
4. нерациональный метод решения задачи или недостаточно продуманный план устного ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
5. нерациональные методы работы со справочной литературой;
Недочетами являются:
1. нерациональные приёмы вычислений и преобразований;
2. ошибки в вычислениях (арифметические);
3. небрежное выполнение записей, чертежей, схем, графиков;
4. орфографические и пунктуационные ошибки.
СОДЕРЖАНИЕ ПРОГРАММЫ:
Содержание программы определено с учетом подготовки к ЕГЭ. Для ОУ и классов данный курс отвечает как требованиям стандарта математического образования, так и требованиям КИМов ЕГЭ.
- Повторение материала курса 10 класса - 5ч.
(Тригонометрические функции. Тригонометрические уравнения. Преобразование тригонометрических выражений. Производная).
- Степени и корни. Степенные функции - 18ч.
Понятие корня n-й степени из действительного числа. Функции у = 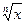 , их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы.
, их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы.
Обобщение понятия о показателе степени. Степенные функции, их свойства и графики.
- Показательная и логарифмическая функции - 29ч.
Показательная функция, её свойства и график. Показательные уравнения. Показательные неравенства.
Понятие логарифма. Логарифмические уравнения. Логарифмические неравенства. Переход к новому основанию логарифма.
- Первообразная и интеграл - 8ч.
Первообразная. Определённый интеграл.
- Элементы математической статистики, комбинаторики и теории вероятностей - 15ч.
Статистическая обработка данных. Простейшие вероятностные задачи. Сочетания и размещения. Формула бинома Ньютона. Случайные события и их вероятности.
- Уравнения и неравенства. Системы уравнений и неравенств - 20ч.
Равносильность уравнений. Общие методы решения уравнений: замена уравнения h(f(x)) = h(g(x)) уравнением f(x) = g(x), разложение на множители, введение новой переменной, функционально-графический метод.
Решение неравенств с одной переменной. Равносильность неравенств, системы и совокупности неравенств, иррациональные неравенства, неравенства с модулями.
Системы уравнений. Уравнения и неравенства с параметрами.
- Обобщающее повторение - 7ч.
Выражения и преобразования. Уравнения и системы уравнений. Неравенства. Функции. Производная. Первообразная. Текстовые задачи. Задачи с параметром.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № | Название раздела, темы | Количество часов (всего) | Из них (количество часов) | |
| Практические работы | Контрольные работы | |||
| Повторение материала курса 10 класса | ||||
| Глава 6. Степени и корни. Степенные функции. | ||||
| Глава 7. Показательная и логарифмическая функции | ||||
| Глава 8. Первообразная и интеграл | ||||
| Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей. | ||||
| Глава 10. Уравнения и неравенства. Системы уравнений и неравенств | ||||
| Повторение | - | |||
| Итого: |
График контрольных работ
| № п/п | Вид и тема работы | Дата проведения (по плану) |
| Административная входная контрольная работа | ||
| Контрольная работа № 1 «Степени и корни . Степенные функции» | ||
| Контрольная работа № 2 «Степенная и показательная функция» | ||
| Контрольная работа № 3 «Понятие логарифма. Логарифмические уравнения | ||
| Контрольная работа № 4 «Логарифмические неравенства. Дифференцирование показательной и логарифмической функции» | ||
| Контрольная работа № 5 «Первообразная и интеграл» | ||
| Контрольная работа № 6 «Элементы математической статистики, комбинаторики и теории вероятностей» | ||
| Контрольная работа № 7 «Уравнения и неравенства. Системы уравнений и неравенств» |
КАЛЕНДАРНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № урока | Тема урока | Дата проведения (по плану) | Дата фактического проведения |
| Повторение материала курса 10 класса – 5ч. | |||
| Повторение. Тригонометрические функции. Тригонометрические выражения. | |||
| Повторение. Тригонометрические уравнения. Преобразование тригонометрических уравнений. | |||
| Повторение. Производная. | |||
| Повторение. Методы решения уравнений. Подготовка к контрольной работе | |||
| Административная входная контрольная работа | |||
| Степени и корни. Степенные функции – 18ч. | |||
| Понятие корня n-ой степени из действительного числа | |||
| Понятие корня n-ой степени из действительного числа | |||
Функции y = 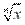 , их свойства и графики , их свойства и графики | |||
Функции y = 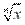 , их свойства и графики , их свойства и графики | |||
Функции y = 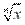 , их свойства и графики , их свойства и графики | |||
| Свойства корня n-ой степени | |||
| Свойства корня n-ой степени | |||
| Свойства корня n-ой степени | |||
| Преобразование выражений, содержащих радикалы | |||
| Преобразование выражений, содержащих радикалы | |||
| Преобразование выражений, содержащих радикалы. Подготовка к контрольной работе. | |||
| 17 | Контрольная работа № 1 «Степени и корни . Степенные функции» | ||
| Анализ контрольной работы. Обобщение понятия о показателе степени | |||
| Обобщение понятия о показателе степени | |||
| Обобщение понятия о показателе степени | |||
| Степенные функции, их свойства и графики | |||
| Степенные функции, их свойства и графики | |||
| Степенные функции, их свойства и графики | |||
| Показательная и логарифмическая функции – 29ч. | |||
| Показательная функция, её свойства и график | |||
| Показательная функция, её свойства и график | |||
| Показательная функция, её свойства и график | |||
| Показательные уравнения и неравенства | |||
| Показательные уравнения и неравенства | |||
| Показательные уравнения и неравенства | |||
| Показательные уравнения и неравенства. Подготовка к контрольной работе. | |||
| 31 | Контрольная работа № 2 «Степенная и показательная функция» | ||
| Анализ контрольной работы. Понятие логарифма | |||
| Понятие логарифма | |||
| Функция y = log a x, её свойства и график | |||
| Функция y = log a x, её свойства и график | |||
| Функция y = log a x, её свойства и график | |||
| Свойства логарифмов | |||
| Свойства логарифмов | |||
| Свойства логарифмов | |||
| Логарифмические уравнения | |||
| Логарифмические уравнения | |||
| Логарифмические уравнения. Подготовка к контрольной работе. | |||
| Контрольная работа № 3 «Понятие логарифма. Логарифмические уравнения» | |||
| Анализ контрольной работы. Логарифмические неравенства | |||
| Логарифмические неравенства | |||
| Логарифмические неравенства | |||
| Переход к новому основанию логарифма | |||
| Переход к новому основанию логарифма | |||
| Дифференцирование показательной и логарифмической функций | |||
| Дифференцирование показательной и логарифмической функций | |||
| Дифференцирование показательной и логарифмической функций. Подготовка к контрольной работе. | |||
| 52 | Контрольная работа № 4 «Логарифмические неравенства. Дифференцирование показательной и логарифмической функции» | ||
| Первообразная и интеграл -8ч. | |||
| Анализ контрольной работы. Первообразная | |||
| Первообразная | |||
| Первообразная | |||
| Определённый интеграл | |||
| Определённый интеграл | |||
| Определённый интеграл | |||
| Определённый интеграл. Подготовка к контрольной работе. | |||
| 60 | Контрольная работа № 5 «Первообразная и интеграл» | ||
| Элементы математической статистики, комбинаторики и теории вероятностей – 15 ч. | |||
| Анализ контрольной работы. Статистическая обработка данных | |||
| Статистическая обработка данных | |||
| Статистическая обработка данных | |||
| Простейшие вероятные задачи | |||
| Простейшие вероятные задачи | |||
| Простейшие вероятные задачи | |||
| Сочетания и размещения | |||
| Сочетания и размещения | |||
| Сочетания и размещения | |||
| Формула бинома Ньютона | |||
| Формула бинома Ньютона | |||
| Случайные события и их вероятности | |||
| Случайные события и их вероятности | |||
| Случайные события и их вероятности. Подготовка к контрольной работе. | |||
| 75 | Контрольная работа № 6 «Элементы математической статистики, комбинаторики и теории вероятностей» | ||
| Уравнения и неравенства. Системы уравнений и неравенств – 20 ч. | |||
| Анализ контрольной работы. Равносильность уравнений | |||
| Равносильность уравнений | |||
| Общие методы решения уравнений | |||
| Общие методы решения уравнений | |||
| Общие методы решения уравнений | |||
| Решение неравенств с одной переменной | |||
| Решение неравенств с одной переменной | |||
| Решение неравенств с одной переменной | |||
| Решение неравенств с одной переменной | |||
| Уравнения и неравенства с двумя переменными | |||
| Уравнения и неравенства с двумя переменными | |||
| Системы уравнений | |||
| Системы уравнений | |||
| Системы уравнений | |||
| Системы уравнений | |||
| Уравнения и неравенства с параметрами | |||
| Уравнения и неравенства с параметрами | |||
| Уравнения и неравенства с параметрами. Подготовка к контрольной работе. | |||
| 94 | Контрольная работа № 7 «Уравнения и неравенства. Системы уравнений и неравенств» | ||
| Повторение – 9 ч. | |||
| Анализ контрольной работы. Повторение. Числа, корни и степени. Модуль (абсолютная величина числа). | |||
| Повторение. Преобразование выражений. | |||
| Повторение. Рациональные уравнения и неравенства. Решение систем уравнений с двумя переменными. | |||
| Повторение. Иррациональные уравнения. | |||
| Повторение. Системы неравенств с одной переменной. Решение неравенств с двумя переменными и их систем. | |||
| Повторение. Преобразование тригонометрических выражений. Тригонометрические уравнения. | |||
| Повторение. Показательные и логарифмические уравнения и неравенства. | |||
| Повторение. Функции и их свойства. Исследование функций с помощью производной. Первообразная и интеграл. |
Базовый учебник
1. Мордкович, А. Г. Алгебра и начала анализа.10-11 классы: учебник / А. Г. Мордкович. - М.: Мнемозина, 2014.
2. Мордкович, А. Г. Алгебра и начала анализа. 10-11 классы: задачник / А. Г. Мордкович, Т. Н. Мишустина, Е. Е. Тульчинская. - М.: Мнемозина, 2014.
Основная литература .
1. Александрова, Л. А. Алгебра и начала анализа. Самостоятельные работы 10-11класс / Л. А. Александрова. - М.: Мнемозина, 2014.
2. Мордкович, А. Г. Алгебра и начала анализа. 10-11 классы. Контрольные работы / А. Г. Мордкович, Е. Е. Тульчинская. - М.: Мнемозина, 2014.
Дополнительная литература
1.Готовимся к ЕГЭ. Задачи с параметрами. Иррациональные уравнения, неравенства, системы, задачи с модулем./ В.В.Локоть / М: Аркти, 2015.
2.А.П.Ершова «Алгебра и начала анализа 10-11 классы. Самостоятельные и контрольные работы», М., «Илекса»,2014
3.Математика: еженедельное приложение к газете «Первое сентября».
4. Математика в школе: ежемесячный научно-методический журнал.
5.Пособия с КИМами ЕГЭ.
Список литературы для учителя.
А.Г Мордкович, П.В Семёнов. Алгебра и начала анализа 10-11 класс. Методическое пособие для учителя, 2014
Список литературы для обучающихся
1. Кукушкин Б.Н. «Подготовка к олимпиадам. Математика. 7-11 классы» -М.: Айрис-пресс, 2011.
2. Л.А. Александрова "Алгебра-11.Самостоятельные работы" / Под ред. А.Г. Мордковича; -М.: Мнемозина, 2015.
3. А.Г. Мордкович, Е.Е. Тульчинская "Алгебра, 10-11 Тесты" - М.: Мнемозина, 2015.
4. Галкин Е.В. «Задачи с целыми числами. 7-11 классы: пособие для учащихся общеобразоват. учреждений - М.: Просвещение, 2012.
5. «ЕГЭ.Тематические тесты.» / Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на Дону: Легион – М, 2016.
Технические средства обучения:
· мультимедийный компьютер;
· мультимедиапроектор;
· экран (на штативе или навесной);
· интерактивная доска.
Информационные средства:
· коллекция медиаресурсов,
· электронные базы данных;
· интернет.
Учебно-практическое и учебно-лабораторное оборудование:
· доска магнитная с координатной сеткой;
· комплект чертёжных инструментов (классных и раздаточных): линейка, транспортир, угольник (30 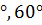 ), угольник (45
), угольник (45  ,45
,45  ), циркуль;
), циркуль;
· комплекты планиметрических и стереометрических тел (демонстрационный и раздаточный);
· комплекты для моделирования (цветная бумага, картон, калька, клей, ножницы, пластилин).
Печатные пособия:
· таблицы по математике для 7-9 классов;
· портреты выдающихся деятелей математики.
02.04
Муниципальное бюджетное общеобразовательное учреждение
«Золотухинская средняя общеобразовательная школа»
Золотухинского района Курской области
| Рассмотрена на заседании педагогического совета протокол № __ от « ___» _________ 2017 г. | Утверждена приказом № __ от «__» ______ 2017 г. Директор школы ________________ В.В. Перьков |
РАБОЧАЯ ПРОГРАММА
по учебному предмету «Математика
(алгебра и начала математического анализа)»
для 11 А класса
среднее общее образование
базовый уровень
2017 - 2018 учебный год
Составлена учителем
высшей квалификационной категории
Семенихиной Л. М.
2017 г.
СТРУКТУРА РАБОЧЕЙ ПРОГРАММЫ
1.Пояснительная записка.
2.Содержание программы.
3.Учебно-тематический план.
4.График контрольных работ.
5.Календарно-тематический план.
6.Ресурсное обеспечение программы.
7.Лист корректировки рабочей программы
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа составлена в соответствии с
1. Государственным стандартом общего образования (2004г).Программа детализирует и раскрывает содержание стандарта, определяет общую стратегию обучения, воспитания и развития учащихся средствами учебного предмета в соответствии с целями изучения математики, которые определены стандартом.
Рабочая программа составлена также на основе авторской программы
А.Г. Мордковича по алгебре и началам математического анализа для общеобразовательных учреждений (базовый уровень) (М.: Мнемозина, 2014).
Выбор данной программы мотивирован тем, что она разработана в соответствии с требованиями федерального компонента государственного стандарта среднего общего образования по математике, обеспечена учебно-методическим комплектом «Алгебра и начала математического анализа» для 11 классов (авторы А.Г. Мордкович и др. (М.: Мнемозина)). Программа призвана содействовать формированию культурного человека, умеющего мыслить, понимающего идеологию математического моделирования реальных процессов, владеющего математическим языком, как языком, организующим деятельность, умеющего самостоятельно добывать информацию и пользоваться ею на практике, владеющего литературной речью и умеющего в случае необходимости построить ее по законам математической речи.
В программе определена последовательность изучения материала в рамках стандарта для средней школы и пути формирования знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования, а также развития учащихся.
Из основных содержательно-методических линий школьного курса алгебры приоритетной в программе является функционально-графическая линия.
В рабочей программе учтены идеи и положения Концепции духовно-нравственного развития и воспитания личности гражданина России, Программы развития и формирования универсальных учебных действий, которые обеспечивают формирование российской гражданской идентичности, овладения ключевыми компетенциями, составляющими основу для саморазвития и непрерывного образования, целостность общекультурного, личностного и познавательного развития учащихся, и коммуникативных качеств личности.
Рабочая программа ориентирована на УМК:
1. Мордкович, А. Г. Алгебра и начала анализа.10-11 классы: учебник / А. Г. Мордкович. - М.: Мнемозина, 2014.
2. Мордкович, А. Г. Алгебра и начала анализа. 10-11 классы: задачник / А. Г. Мордкович, Т. Н. Мишустина, Е. Е. Тульчинская. - М.: Мнемозина, 2014.
Место учебного предмета в образовательном процессе:
Согласно учебному плану МБОУ «Золотухинская средняя общеобразовательная школа» на изучение алгебры и начал анализа отводится 102 часа в год, из расчета 3 часа в неделю.
Уровень изучения учебного предмета: базовый.
Актуальность учебного предмета:
Курс алгебры и начал математического анализа для 11 класса способствует формированию мировоззренческой, гражданской позиций учащихся, расширяет их представление о математике как универсальном языке науки, средства моделирования явлений и процессов, об идеях и методах математики, помогает интеллектуальному и общекультурному развитию школьников. Курс обладает большим познавательным, нравственным и воспитательным значением. При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства». Вводится линия «Начала математического анализа». В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Задачи III ступени образования:
Задачами среднего (полного) общего образования являются развитие интереса к познанию и творческих способностей обучающегося, формирование навыков самостоятельной учебной деятельности на основе дифференциации обучения. В дополнение к обязательным предметам вводятся предметы по выбору самих обучающихся в целях реализации интересов, способностей и возможностей личности.
Основная идея курса:
Программа рассчитана на обучение учащихся 11 классов общеобразовательных классов.
В связи с реальной необходимостью в наши дни большое значение приобрела проблема полноценной базовой математической подготовки учащихся. Учащиеся 11 классов определяют для себя значимость математики, её роли в развитии общества в целом. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Интерес к вопросам обучения математики обусловлен жизненной необходимостью выполнять достаточно сложные расчёты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приёмами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Огромную важность в непрерывном образовании личности приобретают вопросы, требующие высокого уровня образования, связанного с непосредственным применением математики. Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Особенность изучаемого курса состоит в формировании математического стиля мышления, проявляющегося в определённых умственных навыках.
Использование в математике нескольких математических языков даёт возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые средства.
Математическое образование вносит свой вклад в формирование общей культуры человека: знакомство с методами познания действительности (понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач). Изучение математики развивает воображение, пространственные представления. История развития математического знания даёт возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры.
Обучение математики в средней школе направлено на достижение следующих целей:
1) в направлении личностного развития
• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
• воспитание качеств личности, обеспечивающих социальную мобил
