Учет ограничений на параметры
Ограничения на параметры как функционалы задачи могут не иметь производных Фреше и могут дифференцироваться лишь по направлениям в функциональном пространстве (по Гато). Функционалы, соответствующие таким ограничениям, записываются следующим образом:
 , (6.38)
, (6.38)
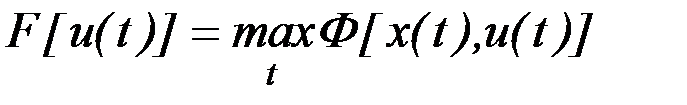 . (6.39)
. (6.39)
Предположим, что для опорного управления максимальное значение функции 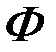 или ее интеграла достигается на отрезке
или ее интеграла достигается на отрезке  в момент времени
в момент времени  . Трудность вычисления производных функционалов вида (6.38) и (6.39) заключается в том, что при изменении управляющей зависимости
. Трудность вычисления производных функционалов вида (6.38) и (6.39) заключается в том, что при изменении управляющей зависимости  на каждой итерации поиска меняется не только максимальное значение функции
на каждой итерации поиска меняется не только максимальное значение функции 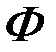 или ее интеграла, но и время его достижения
или ее интеграла, но и время его достижения  .
.
Преобразование исходной задачи в конечномерную позволяет при численном решении аппроксимировать функционалы, дифференцируемые по Гато, несколькими функционалами, дифференцируемыми по Фреше.
В общем случае такая замена производится неоднозначно. Очевидно, что в результате использования этой методики размерность задачи линейного программирования, к многократному решению которой сводится процесс улучшения управления, существенно возрастает в соответствии с увеличением общего числа рассматриваемых функционалов.
В некоторых случаях при формировании управления движением каждый функционал, дифференцируемый по Гато, можно заменять только одним функционалом, дифференцируемым по Фреше. Это позволяет упростить численную процедуру поиска улучшенного управления в условиях наличия многочисленных ограничений вида (6.38) и (6.39).
В соответствии с этим подходом на каждой итерации решения задачи линейного программирования функционалы вида (6.38) и (6.39) заменяются соответственно одним функционалом вида (6.15) или (6.10). Для этого при численном интегрировании траектории движения вычисляются значения функции 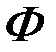 или ее интеграла на отрезке
или ее интеграла на отрезке  и фиксируются их максимальные значения и соответствующие этим значениям моменты времени
и фиксируются их максимальные значения и соответствующие этим значениям моменты времени  .
.
В зависимости от вида функции 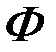 предлагаются два способа учета ограничений на максимальные значения контролируемых параметров траектории.
предлагаются два способа учета ограничений на максимальные значения контролируемых параметров траектории.
Первый способ реализуется для функционалов вида (6.38) при их замене на функционал вида (6.15), а также для функционалов вида (6.39) в том случае, если функция 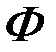 имеет вид аналитического выражения, явно не зависящего от управления, то есть, если функционал (6.39) заменяется на функционал вида (6.10).
имеет вид аналитического выражения, явно не зависящего от управления, то есть, если функционал (6.39) заменяется на функционал вида (6.10).
В этом случае расчет производных осуществляется в соответствии с методикой дифференцирования функционалов вида (6.15) или (6.10). Если значение функционала выходит за пределы назначенного ему ограничения, то каждый компонент вектора управления 
 заменяется в каждом узле аппроксимации на отрезке времени
заменяется в каждом узле аппроксимации на отрезке времени  улучшенным по результатам решения задачи линейного программирования (6.16) - (6.18) значением в соответствии с величиной и знаком производной в этом узле. Изменение управления
улучшенным по результатам решения задачи линейного программирования (6.16) - (6.18) значением в соответствии с величиной и знаком производной в этом узле. Изменение управления  на отрезке
на отрезке  ограничивается величиной малой окрестности
ограничивается величиной малой окрестности  , которая является параметром численного метода решения задачи линейного программирования. В общем случае величина малой окрестности
, которая является параметром численного метода решения задачи линейного программирования. В общем случае величина малой окрестности  может быть различной в разных узлах.
может быть различной в разных узлах.
Второй способ реализуется для функционалов вида (6.39) в том случае, если функция 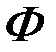 имеет вид аналитического выражения, явно зависящего от управления, то есть, если функционал (6.39) заменяется на функционал вида
имеет вид аналитического выражения, явно зависящего от управления, то есть, если функционал (6.39) заменяется на функционал вида
 . (6.40)
. (6.40)
Улучшение управления на каждой итерации метода последовательной линеаризации производится с учетом возможности непосредственного воздействия на значение контролируемого функционала путем изменения управления в момент времени  .
.
Сначала расчет производных функционалов вида (6.40) осуществляется в соответствии с методикой дифференцирования функционалов вида (6.10). Следует отметить, что для момента времени  в выражении функциональных производных (6.13) для функционалов вида (6.40) по каналам управления, которые оказывают непосредственное влияние на рассматриваемые функционалы, преобладающее значение приобретают производные
в выражении функциональных производных (6.13) для функционалов вида (6.40) по каналам управления, которые оказывают непосредственное влияние на рассматриваемые функционалы, преобладающее значение приобретают производные  , рассчитанные в соответствии с формулами для частных производных функций
, рассчитанные в соответствии с формулами для частных производных функций 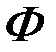 по управлению
по управлению  .
.
Если значение функционала выходит за пределы назначенного ему ограничения, то, как и в предыдущем случае, каждый компонент вектора управления 
 изменяется в каждом узле аппроксимации на отрезке времени
изменяется в каждом узле аппроксимации на отрезке времени  по результатам решения задачи линейного программирования (6.16) - (6.18) в соответствии с величиной и знаком полученных производных функционалов по управлению
по результатам решения задачи линейного программирования (6.16) - (6.18) в соответствии с величиной и знаком полученных производных функционалов по управлению  . Изменение управления
. Изменение управления  ограничивается величиной малой окрестности
ограничивается величиной малой окрестности  .
.
Для узла аппроксимации, соответствующего моменту времени  , компоненты вектора управления изменяются в соответствии со знаком функциональной производной (при численном расчете после проведения конечномерной аппроксимации роль этой производной выполняет соответствующий коэффициент
, компоненты вектора управления изменяются в соответствии со знаком функциональной производной (при численном расчете после проведения конечномерной аппроксимации роль этой производной выполняет соответствующий коэффициент  (6.19)). Однако, допустимое приращение управления по сравнению с величиной малой окрестности
(6.19)). Однако, допустимое приращение управления по сравнению с величиной малой окрестности  существенно увеличивается. Кроме того, поскольку на следующей итерации улучшения управления момент времени
существенно увеличивается. Кроме того, поскольку на следующей итерации улучшения управления момент времени  может изменить свое положение на отрезке
может изменить свое положение на отрезке  , то для соседних узлов допустимое приращение управления также увеличивается.
, то для соседних узлов допустимое приращение управления также увеличивается.
Преобразование задачи к конечномерному виду позволяет в зависимости от ее сложности использовать один из следующих приемов фиксирования момента времени  , соответствующего достижению контролируемым параметром своего экстремального значения.
, соответствующего достижению контролируемым параметром своего экстремального значения.
Первый прием заключается в фиксировании момента времени  после расположения узлов аппроксимации. Этот момент времени выбирается соответствующим узлу с экстремальной величиной функции
после расположения узлов аппроксимации. Этот момент времени выбирается соответствующим узлу с экстремальной величиной функции 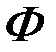 или ее интеграла. При этом расположение узлов на исследуемом участке траектории производится из соображений, не связанных с проблемами аппроксимации функционалов, дифференцируемых по Гато. В этом случае точность фиксирования положения функционала на отрезке
или ее интеграла. При этом расположение узлов на исследуемом участке траектории производится из соображений, не связанных с проблемами аппроксимации функционалов, дифференцируемых по Гато. В этом случае точность фиксирования положения функционала на отрезке  определяется частотой расположения узлов аппроксимации.
определяется частотой расположения узлов аппроксимации.
Второй прием заключается в фиксировании момента времени  в процессе численного интегрирования траектории движения. В этом случае после расположения основных узлов аппроксимации в множество узлов включается дополнительный, момент времени
в процессе численного интегрирования траектории движения. В этом случае после расположения основных узлов аппроксимации в множество узлов включается дополнительный, момент времени  которого соответствует экстремальному значению функции
которого соответствует экстремальному значению функции 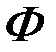 или ее интеграла. В этом случае точность фиксирования положения функционала определяется величиной шага интегрирования траектории движения.
или ее интеграла. В этом случае точность фиксирования положения функционала определяется величиной шага интегрирования траектории движения.
