Метод последовательной линеаризации
Математическая модель движения задана в виде системы обыкновенных дифференциальных уравнений
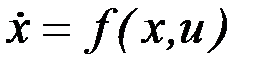 (6.1)
(6.1)
с начальным условием
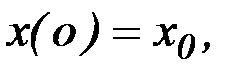 (6.2)
(6.2)
где  - вектор-функция правых частей уравнений движения размерности
- вектор-функция правых частей уравнений движения размерности  ,
,  - вектор фазовых координат размерности
- вектор фазовых координат размерности  ,
,  - вектор управляющих зависимостей размерности
- вектор управляющих зависимостей размерности  .
.
Требуется определить управление  на отрезке времени
на отрезке времени  для системы (6.1) с начальным условием (6.2), удовлетворяющее ограничениям на управление
для системы (6.1) с начальным условием (6.2), удовлетворяющее ограничениям на управление

 при всех
при всех  , (6.3)
, (6.3)
ограничениям на функционалы

 (6.6)
(6.6)
и минимизирующее функционалы
 . (6.5)
. (6.5)
Функционалы 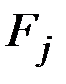
 и
и 
 рассматриваются как неявные зависимости управляющих воздействий
рассматриваются как неявные зависимости управляющих воздействий  , поэтому в общем случае запись
, поэтому в общем случае запись  выражает принципиальную возможность вычислить
выражает принципиальную возможность вычислить  по известной зависимости
по известной зависимости  .
.
Рассмотренная задача в частных случаях приводится к основной задаче управления [18], задаче оптимизации управления или многокритериальной задаче.
Метод последовательной линеаризации предназначен для формирования приближенно-оптимального управления при наличии ограничений на функционалы задачи и управляющие зависимости. Метод является типичным методом спуска в пространстве управлений и сводится к построению минимизирующей последовательности управлений. Подробное описание метода последовательной линеаризации, а также вопросов, связанных с его численной реализацией, приведены в [19]. Модификация метода последовательной линеаризации, результаты решения конкретных задач, а также ссылки на работы, результаты которых использованы при написании этого раздела приведены в [23, 24].
Метод последовательной линеаризации состоит в построении последовательности итераций улучшения управления. На каждой итерации вычисляется малое конечное приращение 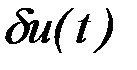 опорного управления
опорного управления  , позволяющее перейти к новому улучшенному опорному управлению
, позволяющее перейти к новому улучшенному опорному управлению  . В начале работы метода задается начальное приближение опорного управления
. В начале работы метода задается начальное приближение опорного управления  , которое затем последовательно улучшается в процессе поиска с целью удовлетворения всем условиям задачи (6.3) - (6.5).
, которое затем последовательно улучшается в процессе поиска с целью удовлетворения всем условиям задачи (6.3) - (6.5).
Если имеется некоторое опорное управление  , то расчет приращения
, то расчет приращения 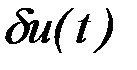 осуществляется следующим образом.
осуществляется следующим образом.
1. Интегрируется система (6.1) с опорным управлением  . Вычисляются опорное решение
. Вычисляются опорное решение  и функционалы задачи
и функционалы задачи 
 , входящие в (6.4) и (6.5).
, входящие в (6.4) и (6.5).
2. Для опорного закона движения  вычисляются функциональные производные
вычисляются функциональные производные  от функционалов
от функционалов  по управлению
по управлению 

 .
.
3. Вводится малая окрестность  опорного управления
опорного управления  . При этом должны быть выполнены следующие требования:
. При этом должны быть выполнены следующие требования:
во-первых, окрестность  опорного управления
опорного управления  должна входить в допустимую область изменения управления
должна входить в допустимую область изменения управления  , то есть
, то есть  ;
;
во-вторых, в окрестности  приращения функционалов
приращения функционалов 
 должны с достаточной точностью описываться формулами первого порядка
должны с достаточной точностью описываться формулами первого порядка
 ;
;
в третьих, окрестность  должна быть не слишком малой,
должна быть не слишком малой,
чтобы обеспечить быстроту процесса перехода от начального приближения опорного управления к искомому, удовлетворяющему условиям задачи (6.3) - (6.5).
4. Определяется приращение  , являющееся решением линейного приближения исходной задачи (6.3) - (6.5) в окрестности опорного закона движения
, являющееся решением линейного приближения исходной задачи (6.3) - (6.5) в окрестности опорного закона движения  . В соответствии с этим
. В соответствии с этим  должно удовлетворять следующим условиям
должно удовлетворять следующим условиям
 при всех
при всех 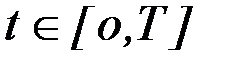 , (6.6)
, (6.6)
 , (6.7)
, (6.7)
 ,
,
 . (6.8)
. (6.8)
5. Проверяется выполнение условий окончания поиска. Если полученное улучшенное управление  удовлетворяет всем условиям исходной задачи (6.3) - (6.4), то поиск искомого управления считается законченным. Если условия не выполняются, то рассчитывается следующая итерация улучшения управления, начиная с пункта 1. В качестве опорного принимается улучшенное управление
удовлетворяет всем условиям исходной задачи (6.3) - (6.4), то поиск искомого управления считается законченным. Если условия не выполняются, то рассчитывается следующая итерация улучшения управления, начиная с пункта 1. В качестве опорного принимается улучшенное управление  .
.
