Статические задачи оптимизации
Статические задачи оптимизации называются также задачами математического программирования.
Задача математического программирования формулируется следующим образом. Найти вектор 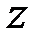 с компонентами
с компонентами 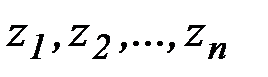 из некоторого допустимого множества
из некоторого допустимого множества 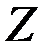 , задаваемого в виде ограничений
, задаваемого в виде ограничений
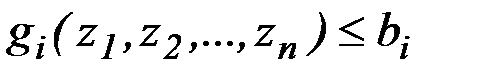
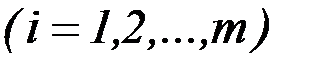 , (1.1)
, (1.1)
который минимизирует (или максимизирует) целевую функцию
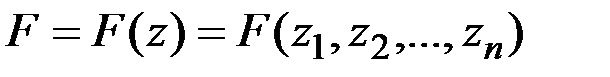 ,
,
т.е.
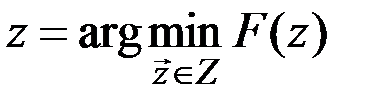 или
или 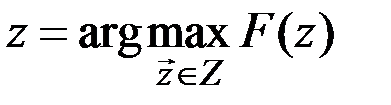 . (1.2)
. (1.2)
В зависимости от вида функций 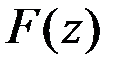 и
и 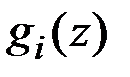 выделены отдельные типы задач, для которых разработаны специальные методы.
выделены отдельные типы задач, для которых разработаны специальные методы.
В классических задачах оптимизации среди ограничений, задающих допустимое множество 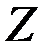 , отсутствуют неравенства, нет условий неотрицательности или дискретности переменных, а функции
, отсутствуют неравенства, нет условий неотрицательности или дискретности переменных, а функции 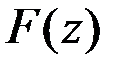 и
и 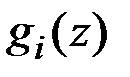 непрерывны и имеют частные производные, по крайней мере, до второго порядка. Типичными задачами являются задачи на отыскание минимума (или максимума) функции
непрерывны и имеют частные производные, по крайней мере, до второго порядка. Типичными задачами являются задачи на отыскание минимума (или максимума) функции 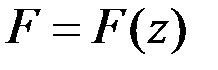 либо в предположении, что на вектор
либо в предположении, что на вектор 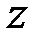 никаких ограничений не накладывается (задачи на безусловный экстремум), либо в предположении, что вектор
никаких ограничений не накладывается (задачи на безусловный экстремум), либо в предположении, что вектор 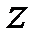 связан только равенствами (задачи на условный экстремум). При решении классических задач оптимизации используется дифференциальное исчисление.
связан только равенствами (задачи на условный экстремум). При решении классических задач оптимизации используется дифференциальное исчисление.
Задачи линейного программирования характеризуются тем, что функции 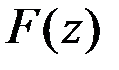 и
и 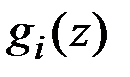 являются линейными по
являются линейными по 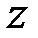 .Требуется найти вектор
.Требуется найти вектор 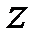 с компонентами
с компонентами 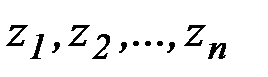 , обеспечивающий минимум (или максимум) функции
, обеспечивающий минимум (или максимум) функции
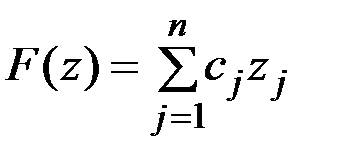 (1.3)
(1.3)
при условиях 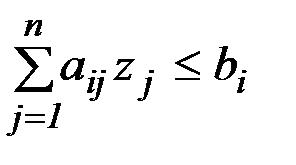
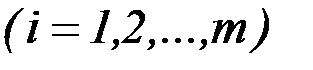 ,
, 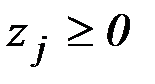
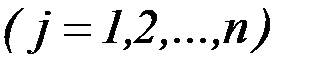 .
.
В основе большинства методов решения задач линейного программирования лежит симплекс-метод [10,12].
К задачам нелинейного программирования относятся все задачи с нелинейной целевой функцией или нелинейными ограничениями. Частным случаем являются задачи квадратичного программирования, которые характеризуются квадратичной зависимостью целевой функции 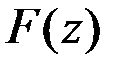 и линейной зависимостью функций
и линейной зависимостью функций 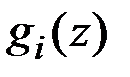 . Методы решения задач этого типа в основном базируются на теореме Куна-Таккера [4].
. Методы решения задач этого типа в основном базируются на теореме Куна-Таккера [4].
В детерминированных задачах целевая функция является детерминированной (неслучайной) функцией параметров. В стохастических задачах параметры являются случайными величинами, а целевая функция представляет собой статистическую характеристику случайной функции параметров.
Для решения задач нелинейного программирования применяются методы поиска, которые, в свою очередь, могут быть детерминированными и стохастическими.
Детерминированные методы поиска имеют жесткий алгоритм поиска (без случайных элементов). К этим методам относятся градиентные методы, метод поочередного изменения параметров, метод штрафных функций, овражные методы, одномерные методы поиска и другие.
Методы случайного поиска характеризуются наличием элемента случайности в алгоритме поиска (например, случайными могут быть величины пробного шага, рабочего шага и другие). К этим методам относятся методы ненаправленного случайного поиска, комбинированные методы поиска, методы случайного поиска с самообучением.
