Задачи и методы классического вариационного

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ

УНИВЕРСИТЕТ имени академика С.П. КОРОЛЁВА

(Национальный исследовательский университет)»

Программа повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013-2020 годы

Ю.Н. Лазарев

СОВРЕМЕННАЯ ТЕОРИЯ

ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Электронное учебное пособие

Самара, 2015

Содержание

Введение…………………………………………………………..…. 4

1. Классификация задач оптимизации………..…………………. 7

1.1. Статические задачи оптимизации ……………...….……….. 7

1.2. Динамические задачи оптимизации ………….…....……….. 8

КЛАССИФИКАЦИЯ ЗАДАЧ ОПТИМИЗАЦИИ

ЗАДАЧИ И МЕТОДЫ

КЛАССИЧЕСКОГО ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ

Необходимое условие экстремума функционала

Рассмотрим некоторый функционал и его приращение , где - вариация .

Определение. Вариацией функции , принадлежащей определенному классу функций, называется разность между двумя функциями при одинаковом значении аргумента : .

Определение. Если можно представить в виде

, (2.4)

где при , то линейная по отношению к часть приращения функционала, т.е. , называется вариацией функционала и обозначается .

Функционал достигает экстремума при , если величина приращения функционала сохраняет свой знак в некоторой окрестности . Различают сильный и слабый экстремумы.

Если существует величина , что сохраняет знак для всех , входящих в пространство (класс) , у которых норма , то говорят, что при достигается слабый экстремум функционала. Аналогично, экстремум называется сильным, если сохраняет знак для всех и удовлетворяет условию . Всякий сильный экстремум будет одновременно и слабым, а слабый сильным быть не может, так как достигается на более узком множестве функций.

Теорема. Для того, чтобы функционал достигал экстремума при , необходимо, чтобы при .

Доказательство

Пусть функционал имеет минимум при , тогда

.

С другой стороны .

При достаточно малом знак определяется знаком , а в силу линейности имеем: . Следовательно, может быть и меньше и больше 0 при сколь угодно малом разного знака, т.е. экстремум невозможен. Противоречие устраняется, если . Аналогично доказывается необходимое условие максимума функционала.

2.3. Простейшая задача вариационного исчисления

(задача с закрепленными концами). Основная лемма

Вариационного исчисления. Уравнение Эйлера

Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями , .

Лемма. Если для каждой непрерывной функции

,

где функция непрерывна на отрезке , то на том же отрезке.

Доказательство

Предположив, что в точке , лежащей на отрезке , , придем к противоречию. Действительно, из непрерывности функции следует, что если , то сохраняет знак в некоторой окрестности точки ; выбрав функцию также сохраняющую знак в этой окрестности и равную нулю вне этой окрестности, получим

,

так как произведение сохраняет знак на интервале и обращается в нуль вне этого отрезка. Итак, мы пришли к противоречию, следовательно, .

Теорема. Для того, чтобы функционал

,

определенный на множестве непрерывных функций , имеющих непрерывную первую производную и удовлетворяющих граничным условиям , , достигал на экстремума, необходимо, чтобы функция удовлетворяла уравнению Эйлера

, (2.5)

или в развернутом виде

. (2.6)

Доказательство

Получим формулу для первой вариации функционала. Применяя операцию варьирования подынтегрального выражения при условии, что , получим

. (2.7)

Проинтегрируем второе слагаемое по частям и, принимая во внимание, что , получим

. (2.8)

Но поскольку концы экстремали закреплены, то , , и получаем необходимое условие экстремума в виде

. (2.9)

В силу основной леммы вариационного исчисления, поскольку , получаем результат (2.5).

Интегральные кривые уравнения Эйлера называются экстремалями, только на них достигается экстремум рассматриваемого функционала. Чтобы установить, реализуется ли на них в действительности экстремум, и притом максимум или минимум, надо воспользоваться достаточными условиями экстремума.

Краевая задача для уравнения (2.6) с граничными условиями , не всегда имеет решение, а если решение существует, то оно может быть не единственным.

Получим необходимые условия экстремума функционала , зависящего от независимых функций :

при заданных граничных условиях всех функций

, ,..., ,

, ,..., .

Если варьировать одну из функций , оставляя остальные неизменными, то рассматриваемый функционал превращается в функционал, зависящий лишь от одной функции, которая, следовательно, должна удовлетворять уравнению Эйлера

.

Так как это рассуждение применимо к любой функции , то мы получим систему дифференциальных уравнений второго порядка

, (2.10)

определяющих -параметрическое семейство интегральных кривых (экстремалей).

Поле экстремалей

Если на плоскости через каждую точку некоторой области проходит одна и только одна кривая семейства , говорят, что это семейство кривых в области образует собственное поле. Угловой коэффициент касательной к кривой семейства , проходящей через точку , называется наклоном поляв точке : .

Поле называется центральным, если кривые покрывают всю область и нигде не пересекаются кроме одной точки (центра пучка кривых), принадлежащей области .

Если собственное или центральное поле образовано семейством экстремалей некоторой вариационной задачи, то оно называется полем экстремалей.

Говорят, что экстремаль включена в поле экстремалей, если найдено семейство экстремалей , образующее поле, содержащее при некотором значении экстремаль , причем последняя не лежит на границе области .

Известно, что две бесконечно близкие кривые семейства пересекаются в точках -дискриминантной кривой, определяемой уравнениями

, .

Если дуга экстремали не имеет отличных от точки общих точек с -дискриминантной кривой пучка экстремалей, включающего данную экстремаль, то достаточно близкие к дуге экстремали пучка не пересекаются, т.е. образуют в окрестности дуги центральное поле, включающее эту дугу.

Если дуга экстремали имеет отличную от точки общую точку с -дискриминантной кривой пучка экстремалей, то близкие кривые пучка могут пересекаться между собой вблизи точки и, вообще говоря, поля не образуют. Точка называется точкой, сопряженной с точкой и является точкой пересечения двух бесконечно близких кривых семейства .

Условие Якоби. Для построения центрального поля экстремалей с центром в точке , содержащего дугу экстремали, достаточно, чтобы точка , сопряженная с точкой , не лежала на дуге .

Изопериметрическая задача

Изопериметрическими задачами в узком смысле этого слова называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.

В настоящее время изопериметрическими задачами называется значительно более широкий класс задач, а именно, все вариационные задачи, в которых требуется определить экстремум функционала

,

при наличии так называемых изопериметрических условий

,

где - постоянные, а может быть больше, меньше или равно .

Рассмотрим следующую изопериметрическую задачу.

Среди всех кривых , удовлетворяющих условиям , , на которых функционал

,

найти такую, которая дает экстремум функционалу

.

Пусть и имеют непрерывные производные на отрезке . Предположим, что искомая кривая не является экстремалью , тогда имеет место теорема [1].

Теорема. Если кривая обеспечивает экстремум функционала и удовлетворяет условиям , , , но не является экстремалью , то существует такое число , что является экстремалью функционала

. (2.15)

Этот результат используется следующим образом. Составляется уравнение Эйлера для функционала . Получается дифференциальное уравнение второго порядка и находится его общее решение, которое содержит параметр и две произвольные постоянные. Эти три величины определяются из граничных условий и условия .

Уравнение Гамильтона-Якоби

Рассмотрим центральное поле экстремалей с центром в точке для функционала

.

На экстремалях поля функционал превращается в функцию координат второй граничной точки . Воспользуемся выражением для вариации функционала (2.11)

.

(2.29)

С другой стороны .

Для точки : , , тогда

, . (2.30)

Следовательно,

. (2.31)

Это уравнение называется уравнением Гамильтона-Якоби.

В этом случае решение канонической системы равносильно решению дифференциального уравнения в частных производных относительно неизвестной функции

(2.32)

с граничным условием .

2.12. Вторая вариация функционала.

Необходимое условие слабого минимума функционала

Для нахождения необходимого условия слабого минимума функционала введем понятие второй вариации функционала. Функционал имеет вторую вариацию, если его приращение можно представить в виде

, (2.33)

где - линейный относительно вариации функции функционал (первая вариация функционала),

- квадратичный относительно функционал (вторая вариация функционала),

- содержит члены высших порядков малости ( при ).

Теорема. Для того, чтобы функционал достигал своего минимума на кривой , необходимо чтобы выполнялись условия

, . (2.34)

Доказательство

Пусть имеется кривая , которая неограниченно приближается к экстремали . Это означает, что , т.е. кривые сближаются. Тогда , , следовательно, знак определяется знаком . Это означает, что неотрицательность второй вариации обеспечивает минимум функционала.

Получим формулу для второй вариации функционала в задаче с закрепленными концами. Зададим функционал

с граничными условиями . В этом случае первая и вторая вариации функционала определяются формулами

,

. (2.35)

Интегрируя по частям среднее слагаемое в подынтегральном выражении формулы (2.35), получим

.

Тогда с учетом граничных условий получим

. (2.36)

Получим условие, при котором . Если мала, то с учетом граничных условий мала и сама , а если мала , то может быть не мала. Поэтому слагаемое в выражении для играет определяющую роль и знак второй вариации функционала определяется знаком . Следовательно, необходимым условием минимума функционала является условие

. (2.37)

Это условие называется условием Лежандра.

Замечание. Для случая функционалов, зависящих от функций условие Лежандра сводится к требованию положительной определенности матрицы

.

Условие Лежандра, как и условие Эйлера, носит локальный характер, т.е. относится не к кривой в целом, а к ее отдельным точкам и поэтому не является достаточным для экстремума.

ПРИНЦИП МАКСИМУМА

Рис.3.1. Вариации управления

Влияние игольчатого варьирования управления на поведение системы аналогично влиянию короткого импульса (рис. 3.2). Степень влияния импульса определяется площадью 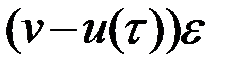. Поскольку эта величина при 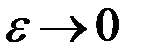становится бесконечно малой, то ее влияние на дальнейшее движение системы бесконечно мало. Малость возмущения позволяет использовать линеаризацию, что упрощает решение задачи, а также рассматривать вариации управления в разные моменты времени независимо друг от друга.

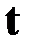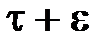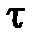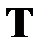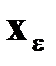Рис.3.2. Влияние игольчатого варьирования управления

на поведение системы

Свойства гамильтониана

На оптимальной траектории гамильтониан обладает следующими свойствами.

1. Гамильтониан 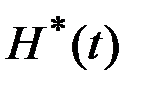- непрерывная функция времени для всех .

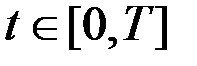Это свойство очевидно для любого , не совпадающего с точками разрыва управления 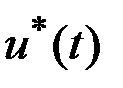. Пусть 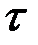- одна из точек разрыва. Рассмотрим значения 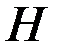слева и справа от точки 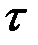. В силу непрерывности по времен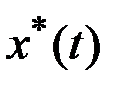и и 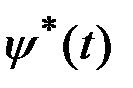можно записать

.

,

.

.

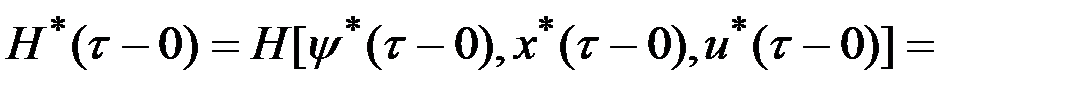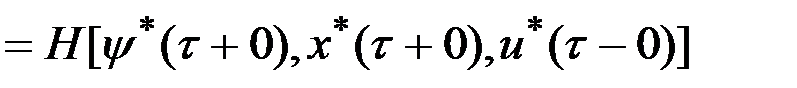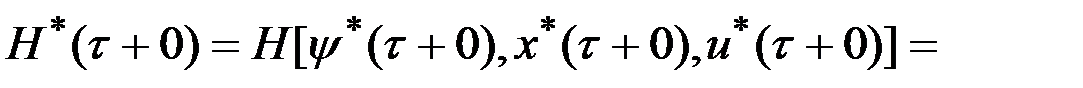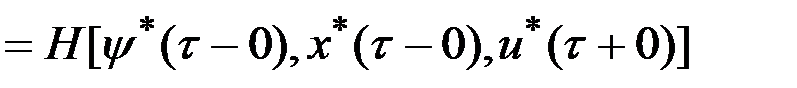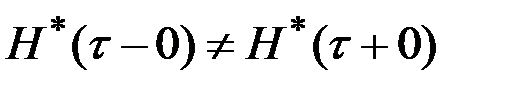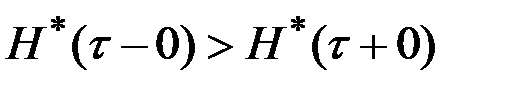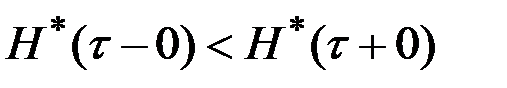Предположим, что . Возможны два случая: и или

.

,

.

.

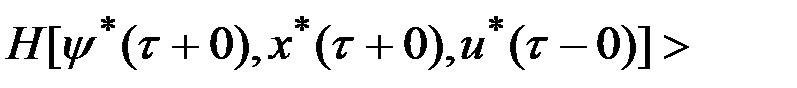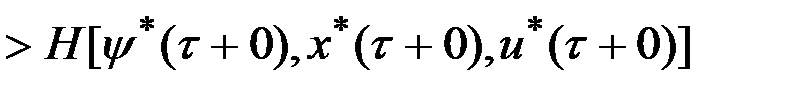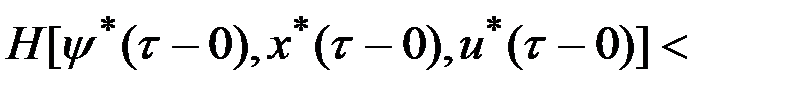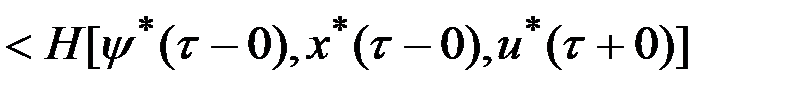И то и другое противоречит основной теореме принципа максимума, согласно которой гамильтониан всегда принимает максимальное значение. Следовательно, 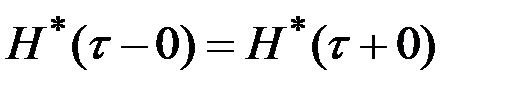, то есть функция 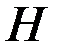непрерывна.

2. Гамильтониан постоянен на оптимальной траектории, т.е. 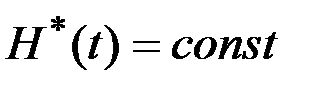для всех .

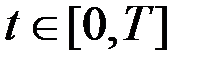Рассмотрим некоторый отрезок 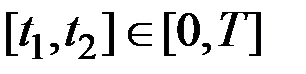, на котором функция 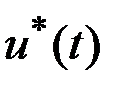непрерывна. Для любых 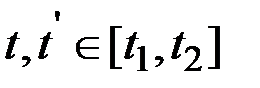в силу основной теоремы принципа максимума

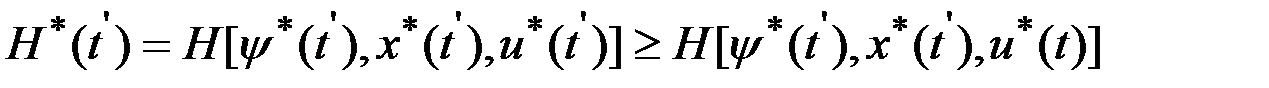
и поэтому

.

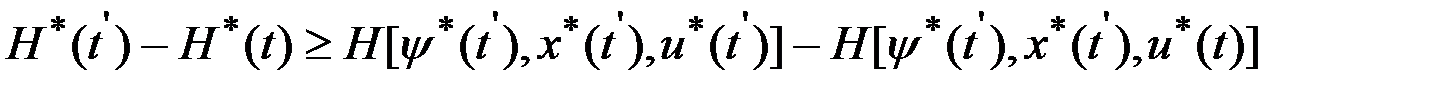Если 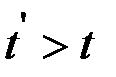, то

.

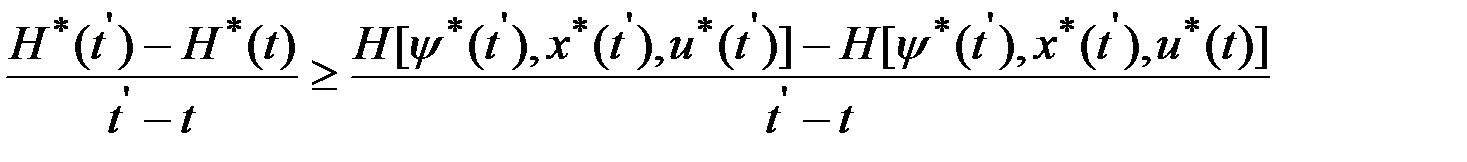При 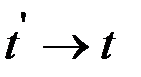получаем неравенство

.

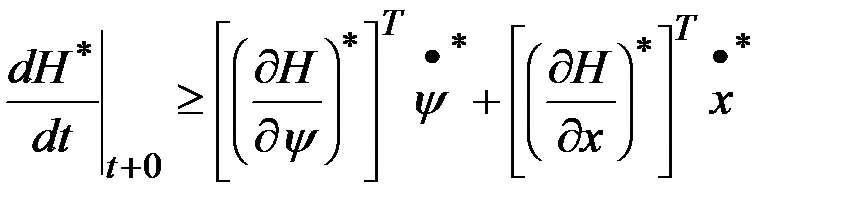Правая часть равна нулю, что следует из канонической системы уравнений. Следовательно,

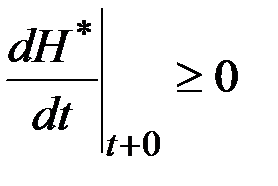. (3.16)

Если 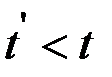, то аналогично можно получить, что

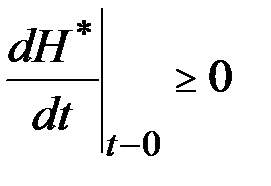. (3.17)

Из (3.16) и (3.17) следует, что 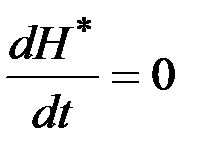, т.е. 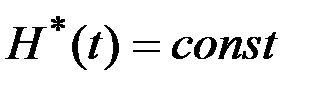для всех 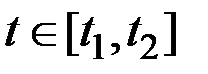. В силу непрерывности 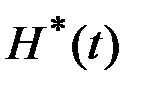по времени 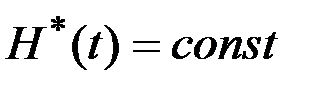для всех .

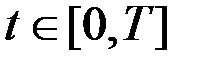3. Если 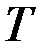свободно, то 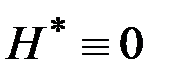для всех .

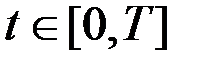Проварьируем управление в конечный момент времени 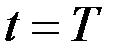, изменив величину 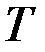на бесконечно малую величину 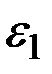и сохранив при этом величину 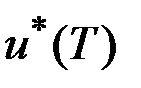. В отличие от игольчатой такая вариация называется временной вариацией управления. Видно, что вариация траектории 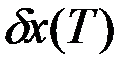с точностью до малых высшего порядка будет равна

.

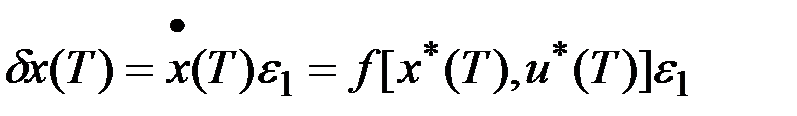Умножив на 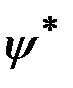с учетом (3.9), получим

.

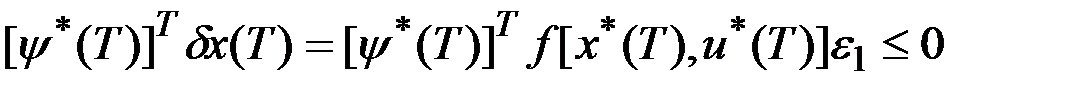Т.к. 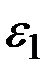может быть положительным и отрицательным, то

.

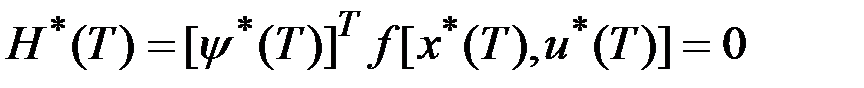Гамильтониан на всей оптимальной траектории постоянен, поэтому

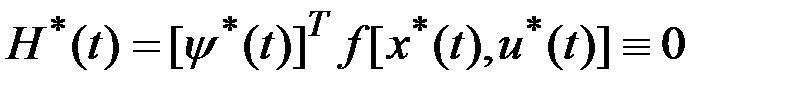
для всех .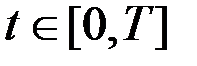

С квадратичным функционалом

1. Задача программирования оптимального управления

Рассмотрим линейную динамическую систему

, , , ,

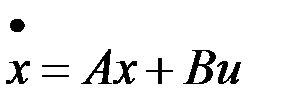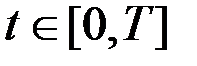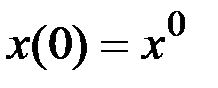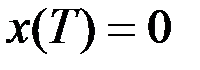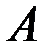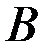где и - матрицы порядков 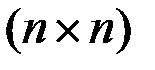и 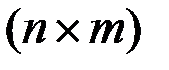, зависящие от времени, 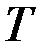- фиксировано, 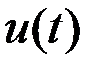- не ограничено.

Критерий оптимальности зададим в виде

,

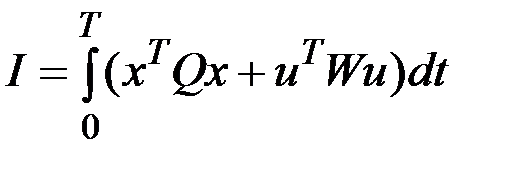где 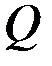и 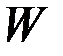- положительно определенные матрицы порядков 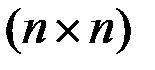и 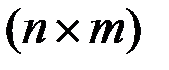, зависящие от времени.

Для определения оптимального управления 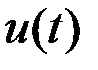, минимизирующего функционал 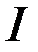, используем принцип максимума, Составим гамильтониан 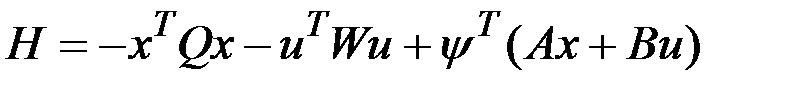. Оптимальное управление определим из условий максимума :

, .

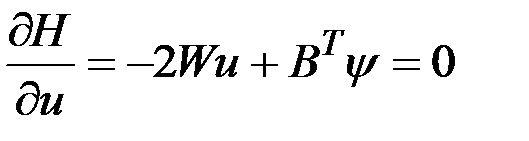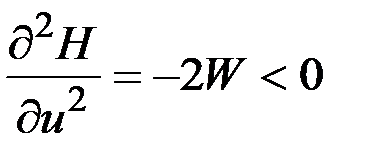Второе условие выполняется, поскольку 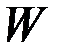- положительно определенная матрица. Следовательно, в соответствии с первым условием оптимальный закон управления имеет вид программы

.

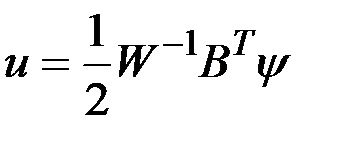Каноническая система уравнений принимает вид

, , ,

.

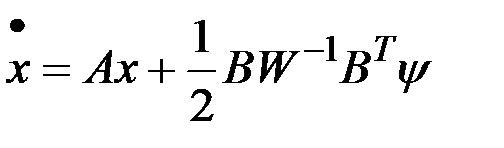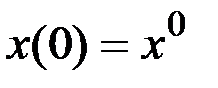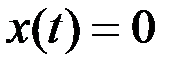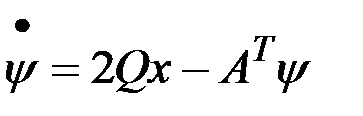Получили краевую задачу для системы линейных дифференциальных уравнений.

2. Задача синтеза оптимального управления

Рассмотрим задачу синтеза оптимального управления системой

, ,

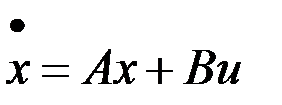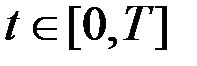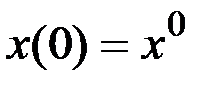
из условия обращения в минимум критерия оптимальности

.

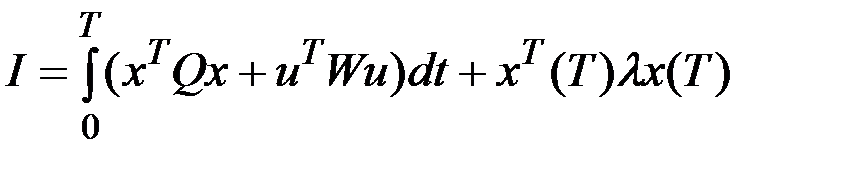Полагаем, что , , , 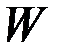- матрицы, зависящие от времени, причем 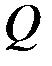, , 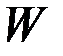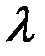- положительно определенные, 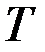- фиксировано.

Как и в предыдущей задаче в соответствии с принципом максимума оптимальное управление определяется зависимостью

.

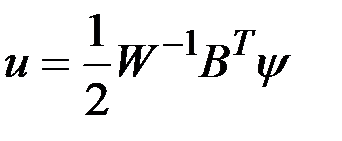Каноническая система уравнений имеет также прежнюю структуру, но другие граничные условия:

, , ,

, .

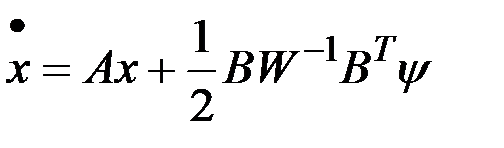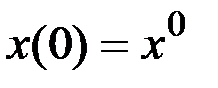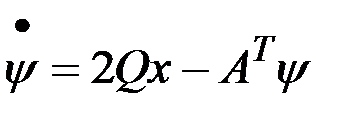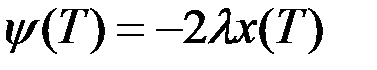Если решение второго уравнения искать в виде 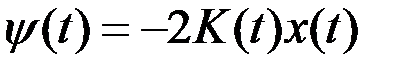, то для матрицы 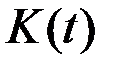можно получить уравнение, которое позволит найти ее непосредственно:

, .

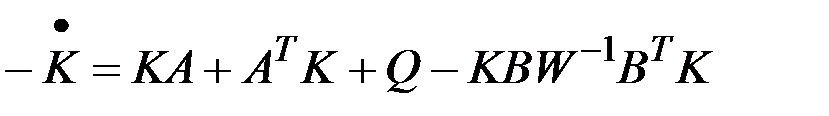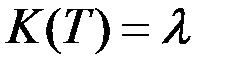Это уравнение представляет собой нелинейное матричное дифференциальное уравнение Риккати. Определив 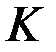, получим закон оптимального управления:

.

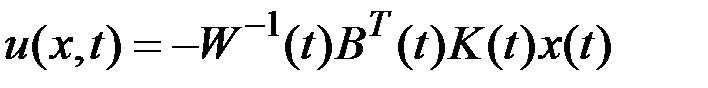Если 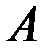, , 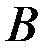, 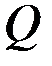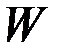не зависят от времени, то при достаточно большом 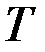можно говорить об «установившемся» режиме. В этом случае полагается 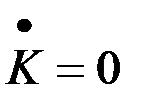. Тогда матрица 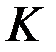является постоянной и определяется из линейного матричного алгебраического уравнения:

.

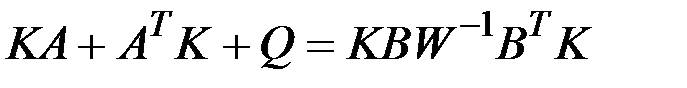Решение этого уравнения можно рассматривать как предел решения дифференциального уравнения Риккати при 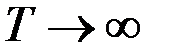, если он существует.

Связь принципа максимума

Уравнение Беллмана

В основе метода динамического программирования лежит принцип оптимальности, сформулированный Р.Беллманом: оптимальный процесс обладает тем свойством, что каким бы ни было начальное управление последующее управление должно быть оптимальным по отношению к состоянию, происходящему от начального управления.

Предположим, что 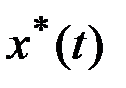- оптимальная траектория, приводящая систему из начального состояния 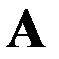в конечное , промежуточное состояние 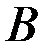соответствует моменту времени 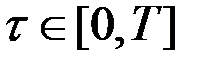(рис.4.1). Согласно принципу оптимальности Беллмана участок траектории 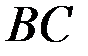представляет собой оптимальную траекторию по отношению к начальному состоянию 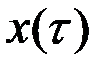, т.е. оптимальное управление на участке 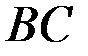не зависит от того, каким образом система приведена в состояние .

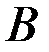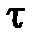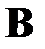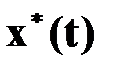Рис.4.1. Оптимальная траектория

Другими словами, каждый участок оптимальной траектории является оптимальной траекторией относительно своей начальной точки, оптимальное управление не зависит от предыстории движения системы и для будущих моментов времени определяется только состоянием в данный момент. Таким образом, всю траекторию движения системы можно разбить на части, двигаясь от ее конца к началу, и оптимизировать движение по частям.

Рассмотрим задачу оптимального управления динамической системой:

, , , , , ,

.

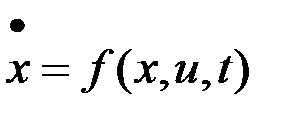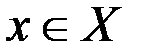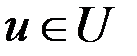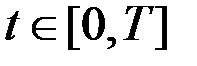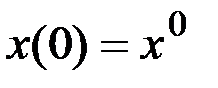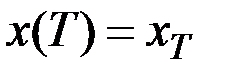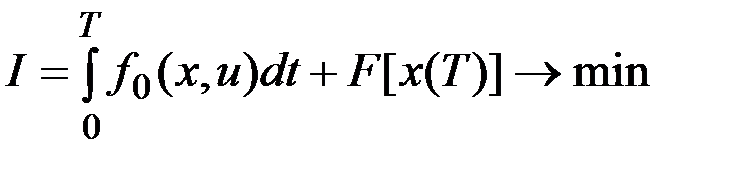Требуется синтезировать закон оптимального управления .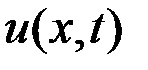

Пусть поставленная задача решена. Введем обозначение: 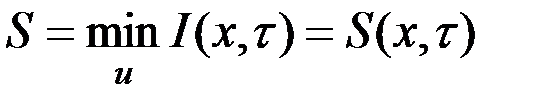- минимальное значение функционала для участка траектории , тогда 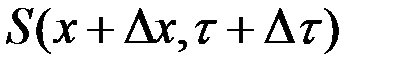- есть минимальное значение функционала 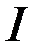для измененного относительно 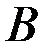состояния и времени. Очевидно, что 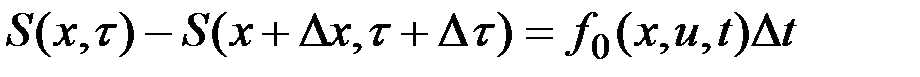. Тогда в общем случае независимых изменений состояния и времени получим в соответствии с принципом оптимальности Беллмана

.

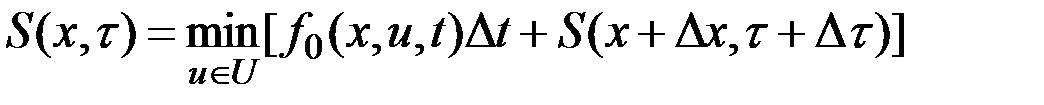Введем допущения о том, что функция 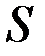непрерыв<