Среднее квадратическое отклонение взвешенное

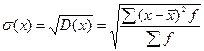
Получим:

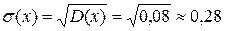– среднее квадратическое отклонение выборки,

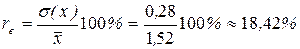– коэффициент вариации.

Среднее квадратическое отклонение показывает, что масса тушек бройлера по данной совокупности колеблется в пределах 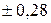кг по отношению к среднему уровню. Коэффициент вариации показывает, что разброс величин (масса тушек) по отношению к среднему уровню средний.

5. Для нахождения моды, медианы и построения гистограммы, полигона, кумуляты построим интервальный ряд распределения (табл.2).

Число групп в ряду распределения определяют по формуле Стерждесса и округляют до целого числа.

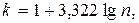
где n – численность совокупности.

Длина интервала должна быть постоянной.

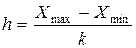
Количество интервалов и длина каждого интервала равны:

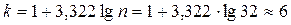
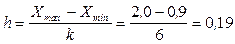
За нижнюю границу первого интервала можно принять .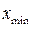

Нижняя граница каждого последующего интервала равна верхней границе предыдущего интервала.

Верхняя граница каждого интервала x_в вычисляется по формуле

x_в = x_н+h,где 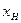– нижняя граница каждого интервала

Середину интервалов определяют по формуле

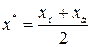
В результате получим Табл.2 (выполним округление до второго знака после запятой).

Табл. 2

№ интервала	Группа тушек по величине хi - масса	Число тушек fi
Нижняя граница Хн	Верхняя граница Хв
	0,9	1,09
	1,09	1,28
	1,28	1,47
	1,47	1,66
	1,66	1,85
	1,85	2,04

f_i – число тушек, попавших в данный интервал.

f_i* – накопленная частота. Определяется как сумма частот предыдущих интервалов и частота текущего интервала.

В результате расчетов (Табл.2) получилось 6 интервалов.

Замечание: интервал, частота которого равна нулю, объединяют с соседним интервалом, который имеет наименьшую частоту. При этом шаг полученного интервала равен сумме шагов объединенных интервалов.

В итоге получим Табл.3.

Табл. 3

№ интервала	Группа тушек по величине хi - масса	Число тушек fi	Середина интервала xi*	Накопленная частота fi*
Нижняя граница Хн	Верхняя граница Хв
	0,9	1,09		0,995
	1,09	1,28		1,185
	1,28	1,47		1,375
	1,47	1,66		1,565
	1,66	1,85		1,755
	1,85	2,04		1,945

6. Средние величины, описанные выше, являются обобщающими характеристиками совокупности по тому или иному признаку. Вспомогательными характеристиками являются, так называемые, структурные средние, к которым относятся мода, квартили, децили, медиана и др. Наиболее употребляемыми являются мода и медиана.

Модальный интервал – интервал с наибольшей частотой.

Мода вычисляется по формуле:

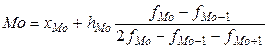
Наибольшая частота f_i = 11 на интервале 1,62 – 1,8. Следовательно, модальным является интервал 1,62 – 1,8.

х_Мо = 1,66

h_Мо = 0,19

f_Мо = 11

f_Мо-1 = 9

f_Мо+1 = 1

Тогда, мода равна:

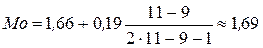
Медианный интервал – интервал, накопленная частота которого равна или превышает половину суммы частот.

Медиана вычисляется по формуле

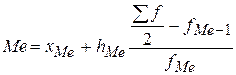
Половина суммы частот равна 16 (32/2). Следовательно, медианным интервалом будет интервал 1,47 – 1,66.

х_Ме = 1,47

h_Ме =0,19

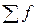= 32

f_Ме−1 = 11

f_Ме = 9.

Тогда, медиана равна:

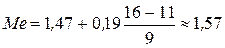
7. Существенную помощь в анализе ряда распределения и его свойств оказывает графическое изображение.

Интервальный ряд отображается гистограммой, в которой ось ОХ – интервалы значений варьирующего признака, а ось OY – частоты.

Если имеется дискретный ряд распределения или используются середины интервалов, то такой ряд отображается в виде полигона -координаты X_i^* (ось ОХ) и f_i. (ось OY).

Кумулятаотображает накопленные частоты, последовательное суммирование (кумуляция) частот в направлении от первого класса до конца вариационного ряда.

По данным Табл. 3 построим гистограмму, полигон и кумуляту (Рис. 6 – 8).

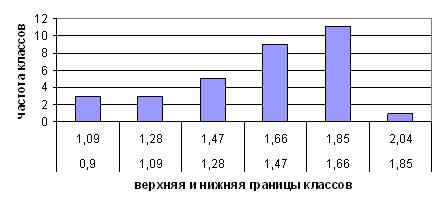
Рис. 6. Гистограмма распределения массы тушек

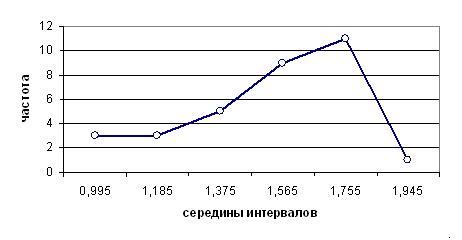
Рис. 7. Полигон распределения массы тушек

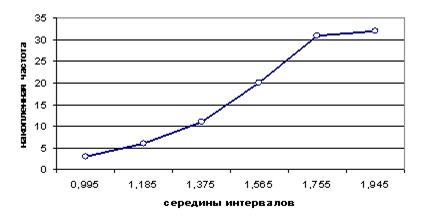
Рис. 8. Кумулята распределения массы тушек

Данные гистограммы и полигона показывают: чаще встречаются тушки бройлера с массой от 1,66 до 1,85 кг, среди них 11 штук имеют среднюю массу 1,755 кг.

Данные кумуляты показывают: количество тушек бройлера с массой до 1,09 кг – 3; с массой до 1,28 кг – 6; с массой до 1,47 кг – 11; с массой до 1,66 кг – 20; с массой до 1,85 кг – 31; с массой до 2,04 кг – 32 штуки.

Для вычисления числовых характеристик асимметрии и эксцесса (A_s, E) составим следующую таблицу:

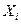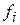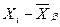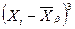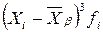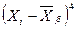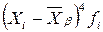0,9		-0,6	-0,216	-0,648	0,1296	0,3888
1,2		-0,3	-0,027	-0,081	0,0081	0,0243
1,4		-0,1	-0,001	-0,005	0,0001	0,0005
1,5
1,6		0,1	0,001	0,007	0,0001	0,0007
1,7		0,2	0,008	0,04	0,0016	0,008
1,8		0,3	0,027	0,162	0,0081	0,0486
		0,5	0,125	0,125	0,0623	0,0625

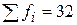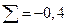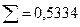Применим формулы для вычисления моментов распределения третьего и четвертого порядков:

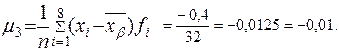
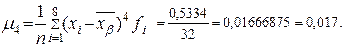
Рассчитаем третью и четвертую степень среднего квадратического отклонения

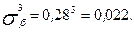
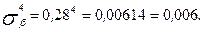
Найдем коэффициент асимметрии и эксцесса:

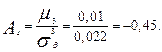
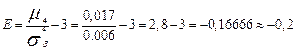
Выводы: коэффициент асимметрии отрицательный, следовательно, имеем левостороннюю асимметрию распределения полигона.

Коэффициент эксцесса отрицательный, следовательно, имеем плосковершинное распределение.

Вопросы для самопроверки

1. Что понимается под генеральной совокупностью?

2. Что такое выборка, объем выборки? Как обеспечивается представительность выборки?

3. Как получают повторную и бесповторную выборки?

4. Перечислите способы отбора статистического материала.

5. Что такое частота появления варианты в выборке?

6. Как получают относительную частоту варианты в выборке?

7. Как получают вариационный ряд распределения?

8. Как графически изображают вариационные ряды?

9. Как построить многоугольник распределения относительных частот?

10. Как построить гистограмму распределения плотностей относительных частот?

11. Дайте определение моды и медианы выборки.

12. В чем сущность задачи по определению параметров генеральной совокупности? В чем особенность этой задачи?

13. Как вычисляется средняя арифметическая выборки при малых и больших ее объемах?

14. Как вычисляется дисперсия выборки в случаях малого и большого ее объемов?

15. Какую величину принимают за среднюю генеральной совокупности?

16. Какую величину принимают за дисперсию генеральной совокупности?

17. Что понимают под доверительным интервалом и доверительной вероятностью?

18. Как вычисляют среднее квадратическое отклонение выборки?

19. Какова вероятность попадания генеральной средней в интервал размером ±2 (±3) средних квадратических отклонения средней выборки при нормальном распределении?

20. Если доверительная вероятность будет увеличена, то как изменится доверительный интервал при других равных условиях?

21. Что надо сделать с объемом выборки, чтобы уменьшить доверительный интервал при том же значении доверительной вероятности?