Законы распределения непрерывной случайной величины

Равномерное распределение.Пусть плотность вероятности равна нулю всюду, кроме отрезка 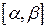, на котором все значения случайной величины Х одинаково возможны. Тогда выражение плотности распределения вероятностей р(х)имеет следующий вид:

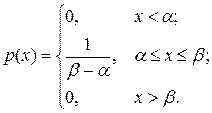(7.1)

Функция равномерного распределения задается формулой:

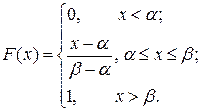(7.2)

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:

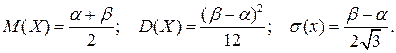(7.3)

Нормальное распределение.Распределение непрерывной случайной величины называется нормальным, если плотность распределения вероятностей описывается формулой:

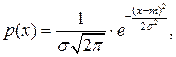(7.4)

где 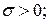m – параметры распределения.

Функция распределения случайной величины Х, распределенной по нормальному закону:

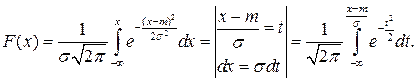(7.5)

Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:

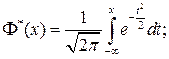( или ),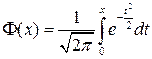

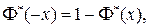
называемую нормальной функцией распределения (функцией Лапласа). Эта функция неубывающая, непрерывная слева 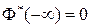и

и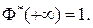

Математическое ожидание и дисперсия нормально распределенной случайной величины Х соответственно равны М(Х)=m; D(Х)=σ².

Центральные моменты случайной величины с нормальным законом распределения вычисляются при помощи следующих рекуррентных соотношений: 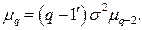Поскольку μ₁=0, то нечетные центральные моменты равны нулю, а четные центральные моменты равны: μ₂=σ², μ₄=Зσ⁴, μ₆=15σ⁶. Коэффициенты асимметрии и эксцесса для нормального закона распределения равны нулю, так как они характеризуют «скошенность» и «крутизну» исследуемого закона распределения по сравнению с нормальным. Вероятность попадания случайной величины Х, подчиненной нормальному закону распределения, на заданный интервал (α, β), определяется следующим образом:

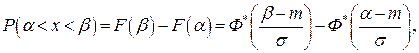
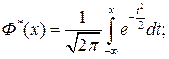(7.6)

или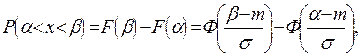

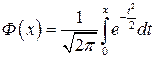– функция Лапласа.

Функция Лапласа удовлетворяет свойствам функции распределения и Ф(0)=0;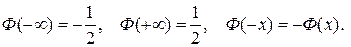

Вероятность заданного отклонения вычисляется по формуле:

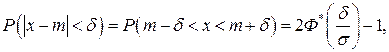или

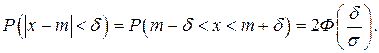(7.7)

Интервалом практически возможных значений случайной величины Х, распределенной по нормальному закону, будет интервал (m–Зσ; m+Зσ).

Показательное распределение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается функцией плотности вероятности:

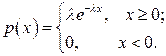(7.8)

где λ > 0 постоянная и называется параметром экспоненциального распределения.

Функция распределения случайной величины, распределенной по показательному закону, имеет вид:

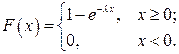(7.9)

Математическое ожидание: 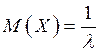. Дисперсия 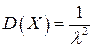, среднее квадратическое отклонение: .

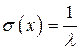Задачи

7.1.Шкала секундомера имеет цену деления 0,2 сек. Считая, что случайная величина Х – ошибка округления, записать ее плотность распределения, функцию распределения. Вычислить М(Х), D(Х), σ(Х)случайной величины Х. Какова вероятность сделать по этому секундомеру отсчет времени с ошибкой более 0,05 сек., если отсчет делается с округлением в ближайшую сторону?

Решенеие. Так как стрелка секундомера двигается скачкообразно и цена деления равна 0,2 сек., то случайная величина Х – ошибка округления, распределена равномерно в интервале (0; 0,2). Воспользуемся формулой (7.1). Тогда плотность распределения вероятностей для случайной величины Х – ошибка округления, запишется в виде:

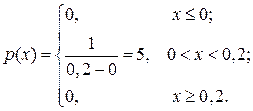
Функция распределения, согласно (7.2), задается формулой:

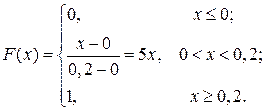
Математическое ожидание, дисперсия и среднее квадратическое отклонение, согласно формулам (7.3), равны:

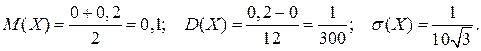
Ошибка в отсчете времени будет больше 0,05 сек., если стрелка секундомера будет «находится» на интервале (0,05; 0,15). А вероятность того, что значения случайной величины Х принадлежат интервалу (0,05; 0,15) вычислим по формуле (6.3):

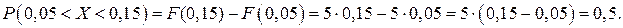
Ответ: вероятность сделать ошибку более 0,05 равна 0,5.

7.2.Автобусы некоторого маршрута идут строго по расписанию, интервал движения 5 минут. Считая, что случайная величина Х – время ожидания автобуса на остановке – распределена равномерно, найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 2 минут.

7.3. Цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

7.4.Шкала рычажных весов, установленных в торговой точке, имеет цену деления 100г. При измерении массы товара отсчет делается с точностью до целого деления с округлением в ближайшую сторону. Какова вероятность, что абсолютная ошибка определения массы: 1) не превысит величины среднеквадратического отклонения возможных ошибок определения массы; 2) будет заключена в пределах от 0 до 3σ(Х)?

7.5.Пациенты заходят в кабинет врача каждые 10 минут. Пусть время ожидания пациентом посещения врача случайная величина Х, которая имеет равномерное распределение. Найти плотность распределения, функцию распределения, математическое ожидание, среднее квадратическое отклонение этой случайной величины Х. Вычислить вероятность того, что пациент будет ожидать посещения врача меньше 3 минут.

7.6.Определить закон распределения случайной величины Х, если ее плотность распределения вероятностей задана функцией:

а) 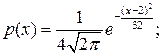б)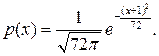

Определить математическое ожидание, дисперсию и функцию распределения.

Решение. а) Поскольку 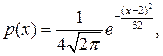то, сравнив эту функцию с формулой (7.4), заключаем, что случайная величина Х распределена по нормальному закону с параметрами т=2; σ=4. Так как параметр т – это математическое ожидание, а σ – среднее квадратическое отклонение нормально распределенной случайной величины, то М(Х)=2, D(Х)=16.

Согласно формуле (7.5) определяем функцию распределения:

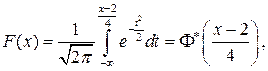
или 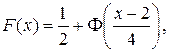где Ф(х) – функция Лапласа.

7.7.Записать плотность распределения вероятностей и функцию распределения нормально распределенной случайной величины Х, если: а) М(Х)=5; D(Х)=9; б) М(Х)=–3; D(Х)=16.

Решение. а) Так как параметры т и σ в формуле плотности распределения вероятностей являются математическим ожиданием и средним квадратическим отклонением нормально распределенной случайной величины Х, то плотность определяется функцией:

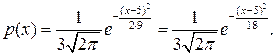
Согласно формуле (7.5) записываем функцию распределения:

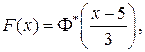или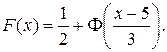

7.8.Известны числовые характеристики М(Х)=6; D(Х)=25 нормально распределенной случайной величины Х. Вычислить вероятность того, что значения случайной величины Х принадлежит полуинтервалу [7;12].

Решение. Для вычисления искомой вероятности воспользуемся формулой (7.6), учитывая, что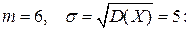

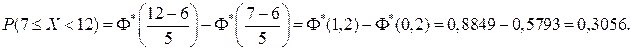
7.9.Математическое ожидание случайной величины Х распределенной по нормальному закону равно 5. Вычислить Р(0≤Х<5), если известно, что Р(0≤Х<10)=0,1.

Решение. Воспользуемся формулой (7.6):

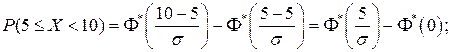
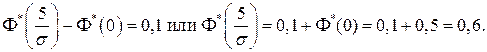
Тогда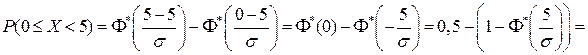

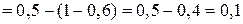(при вычислении 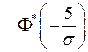воспользовались формулой ).

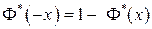Ответ: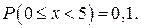

7.10.Станок-автомат изготавливает втулки, которые удовлетворяют стандарту, если отклонение Х от проектного размера по модулю не превышает 0,35 мм. Каково наиболее вероятное число стандартных втулок из 200, если случайная величина распределена нормально с параметром σ=0,2 мм.

Решение. Вначале вычислим вероятность отклонения Х от проектного размера по формуле (7.7), учитывая, что δ=0,35, а σ=0,2:

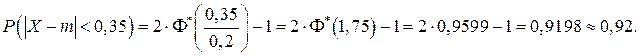
Для определения наиболее вероятного числа m₀ стандартных втулок воспользуемся формулой (5.2), в которой р=0,92; q=1–0,92=0,08, п=200:

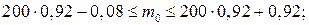
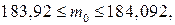откуда т₀ = 184.

Ответ: т₀ = 184.

7.11.Коробки с шоколадом упаковываются автоматически: средняя масса одной коробки – 1,06 кг. Известно, что только 5% коробок имеют массу меньше 1 кг. Найти стандартное отклонение, предполагая, что масса коробок распределена нормально.

Решение. Пусть случайная величина Х – масса коробки с шоколадом. Из условия задачи следует, что случайная величина Х распределена нормально и что М(Х) = 1,06. Тогда стандартное отклонение 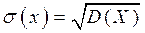найдем, из формулы, используя равенство 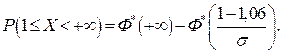Так как только 5% коробок имеют массу меньше 1 кг и, следовательно, масса остальных коробок больше 1 кг, то можно записать:

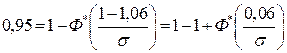или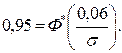

По таблице 1 находим 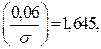откуда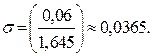

Ответ: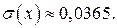

7.12.На автоматическом токарном станке изготавливаются болты, номинальная длина которых 30мм. Наблюдаются случайные отклонения от этого размера, распределенные по нормальному закону с математическим ожиданием m=0 и средним квадратическим отклонением σ = 1мм. При контроле бракуются все болты, размеры которых отличаются от номинального больше, чем на допуск Δ = 3 мм. Найти вероятность того, что наудачу выбранный болт будет бракованный.

7.13.Случайная величина Х подчинена нормальному закону с математическим ожиданием m = 0 и средним квадратическим отклонением σ. При каком значении σ вероятность попадания случайной величины Х в интервал (2; 4) достигает максимума?

7.14.В нормально распределенной совокупности 15% значений Х меньше 12 и 40% значений Х больше 16,2. Найти среднее значение и стандартное отклонение данного распределения.

7.15.Химический завод изготавливает серную кислоту номинальной плотности 1,84 г/см³. В результате статистических испытаний обнаружено, что практически 99,9% всех выпускаемых реактивов имеют плотность в интервале (1,82; 1,86). Найти вероятность того, что кислота удовлетворяет стандарту, если для этого достаточно, чтобы ее плотность не отклонялась от номинальной более, чем на 0,01 г/см³, предполагая, что значение плотности распределено по нормальному закону.

7.16.В пакете 5% всех акций отклоняется от средней цены в 120$ более чем на 2$. Считая, что распределение цены акций подчиняется нормальному закону, найти, какой процент акций имеет цену в пределах от 119 до 121$.

7.17.Вероятность банкротства отдельной фирмы равна 0,75. Основываясь на нормальном законе распределения, определить какова вероятность того, что из 200 фирм обанкротятся не менее 140 и не более 180.

7.18.Станок-автомат изготавливает цилиндры, номинальный диаметр которых равен m=10 мм. Случайная величина Х – величина диаметра, распределена нормально со средним квадратическим отклонением 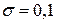. Найти интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных цилиндров.

7.19.100 фирм одной отрасли работают независимо друг от друга. Известно, что каждая фирма обеспечена работой в течение рабочего времени с вероятностью равной 0,8. Определить вероятность того, что в произвольно взятый момент времени будут работать от 70 до 86 фирм, если распределение занятости работой подчиняется нормальному закону.

7.20.Средний процент выполнения плана некоторыми предприятиями составляет 100%, среднее квадратическое отклонение – 9%. Полагая, что выполнение плана этой группой предприятий подчиняются закону нормального распределения, определить процент предприятий: а) не выполняющих план; б) выполняющих план от 110 до 150%.

7.21.Два небольших завода F₁ и F₂ производят некоторый товар. Количество товара Х₁ и Х₂ производимого соответственно заводами F₁ и F₂ за неделю, распределены независимо и можно считать, что они имеют приближенно нормальное распределение. Количество товара Х₁ имеет среднее значение, равное 6000 и дисперсию, равную 900, Х₂ имеет среднее значение, равное 15000 и дисперсию, равную 3600. Товар, производимый на заводе F₁, приносит прибыль 3 ден. ед. в расчете на 1 единицу товара, а товар, производимый на F₂ – 2 ден. ед. Предполагая, что сумма издержек производства заводов составляет 10000 ден. ед. в неделю, найти вероятность того, что за некоторую неделю суммарная чистая прибыль завода будет больше 38500 ден. ед.

7.22.В среднем брак составляет 3%. Какова вероятность того, что в партии из 500 изделий число бракованных не превышает 20? Будем исходить из предложения, что число бракованных изделий в определенных партиях подчиняется нормальному закону распределения.

7.23.При определении доли прибыли допускают случайные ошибки, подчиненные нормальному закону распределения со средним отклонением 10 ден. ед. Найти вероятность того, что определение прибыли будет проведено с ошибкой, не превосходящей 15 ден. ед., если систематические ошибки отсутствуют.

7.24.Деталь, изготовленная станком-автоматом, считается годной, если отклонение ее контролируемого размера от проектного не превышает 1 мм. Случайные отклонения контролируемого размера от проектного подчинены нормальному распределению со средним квадратическим отклонением σ=0,5мм и математическим ожиданием m=0. Сколько процентов годных деталей изготавливает станок-автомат?

7.25.Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону распределения со средним квадратическим отклонением равным 3 мм, а систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготавливаются четыре изделия.

7.26.Как, зная среднее квадратическое отклонение σ и математическое ожидание т случайной величины Х,распределенной по нормальному закону, ориентировочно указать интервал ее практически возможных значений?

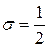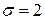7.27.Как изменяется ордината кривой нормального распределения для и при ?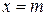

7.28.Непрерывная случайная величина распределена по показательному закону, заданному плотностью распределения вероятностей:

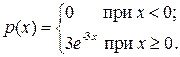
Вычислить функцию распределения, математическое ожидание и дисперсию заданной случайной величины Х. Найти вероятность того, что значение случайной величины принадлежит интервалу (1; 3).

Решение. Воспользовавшись формулой (7.9) запишем функцию распределения:

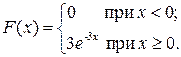
Так как параметр показательного распределения λ=3, то 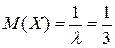; 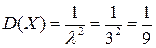. Вероятность попадания Х в интервал (1; 3) равна разности значений функции распределения на концах интервала, т.е.

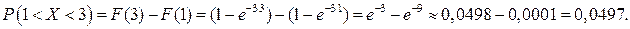
Ответ: .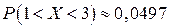

7.29.Функция распределения случайной величины Т времени безотказной работы радиоаппаратуры имеет вид: 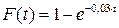, 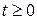. Какому закону распределения подчиняется эта случайная величина Т? Вычислить: а) вероятность безотказной работы радиоаппаратуры в течение времени t=100 ч.; б) вероятность того, что радиоаппаратура откажет в течение времени t=100 ч.

Решение. Воспользовавшись формулой (6.2) определим плотность распределения вероятностей случайной величины Т:

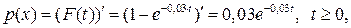
которая совпадает с функцией (7.8). Следовательно, случайная величина Т распределена по показательному закону.

Функция распределения 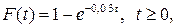определяет вероятность отказа радиоаппаратуры за время длительностью t с интенсивностью отказов (среднее число отказов в единицу времени) равной 0,03.

а) Вероятность безотказной работы радиоаппаратуры в течение времени t=100 ч. равна: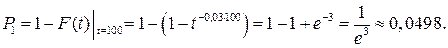

б) Так как функция распределения F(t) определяет вероятность отказа за время длительностью t, то, подставив t=100 в функцию распределения, получим вероятность отказа радиоаппаратуры за время длительностью t=100 ч.:

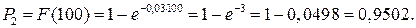
Ответ: Р₁=0,0498; Р₂=0,9502.

7.30.Время ожидания у бензоколонки автозаправочной станции является случайной величиной Х, распределенной по показательному закону со средним временем ожидания, равным 10 минутам. Найти вероятности следующих событий: А = {5≤ Х≤ 15}, В = {X ≥ 20}.

7.31.На шоссе установлен контрольный пункт для проверки технического состояния автомобилей. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Т – времени ожидания очередной машины контролером, если поток машин простейший и время (в часах) между прохождениями машин через контрольный пункт распределено по показательному закону р(t)=5e^–5t.

7.32.Студент помнит, что плотность распределения вероятностей показательного распределения имеет вид:

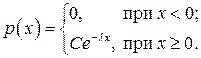
Однако он забыл, чему равна постоянная С. Найти постоянную С.

7.33.Производится испытание двух приборов, работающих независимо друг от друга. Длительность безотказной работы приборов распределена по показательному закону с плотностями распределения 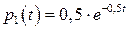, 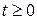; 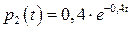, , 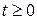соответственно. Найти вероятность того, что в интервале (0; 5) часов откажут: 1) оба прибора; 2) только один прибор; 3) хотя бы один прибор.

7.34.Искусственный спутник земли, движущийся по своей орбите в течение п суток, может случайным образом сталкиваться с метеоритами. Метеориты, пересекающие орбиту и сталкивающиеся со спутником, образуют пуассоновский поток с плотностью h (метеоритов в сутки). Метеорит, попавший в спутник, пробивает его оболочку с вероятностью р₀.Метеорит, пробивший оболочку с вероятностью р₁, выводит из строя аппаратуру спутника. Найти вероятность следующих событий: а) за время полета его оболочка будет пробита; б) за время полета его аппаратура будет выведена из строя; в) за время полета будет пробита оболочка, а аппаратура будет действовать.

7.35.При работе некоторого прибора в случайные моменты времени возникают неисправности. Время Т работы прибора от его включения до возникновения неисправности распределено по показательному закону:

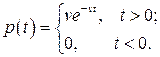
При возникновении неисправности она мгновенно обнаруживается, и прибор поступает в ремонт. Ремонт продолжается время t₀, после чего прибор снова включается в работу. Найти плотность распределения 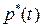и функцию распределения F^*(t) промежутка времени Т^* между двумя последовательными неисправностями. Найти его математическое ожидание и дисперсию. Найти вероятность того, что время Т^* будет больше 2t₀.

7.36.Время t между двумя сбоями в работе вычислительной машины распределено по показательному закону с параметром λ:

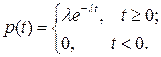
Решение задачи требует безотказной работы машины в течение времени τ. Если за время τ произошел сбой, то задачу приходится решать заново. Сбой обнаруживается только через время τ после начала решения задачи. Найти закон распределения случайной величины Т – времени, за которое задача будет решена.