Непрерывные случайны величины.

Случайная величина Х, которая может принимать все значения из некоторого промежутка, называется непрерывнойслучайной величиной.

Множество значений Ω_х непрерывной случайной величины Х – некоторый числовой интервал.

Плотностью распределения вероятностей р(х) непрерывной случайной величины Х называют предел, если он существует, отношения вероятности попадания случайной величины Х на отрезок [х;х+Δх], примыкающий к точке x, к длине этого отрезка, когда последний стремится к 0, т.е.

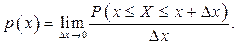
Свойства плотности распределения вероятностей:

1. р(х) – неотрицательная функция, т.е.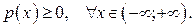

2. Вероятность достоверного события 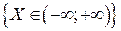равна 1, т.е.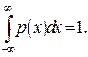

3. р(х) – непрерывная или кусочно-непрерывная функция.

Функция распределения случайной величины Х – это функция Р(х) действительной переменной х, определяющая вероятность того, что случайная величина принимает, значение меньше некоторого фиксированного числа х, т.е. :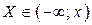

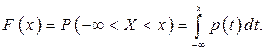(6.1)

Более строгое определение непрерывной случайной величины формулируется следующим образом.

Случайная величина Х называетсянепрерывной, если существует такая неотрицательная, интегрируемая по Риману функция р(х), называемая плотностью распределения вероятностей, что при всех 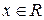выполняется равенство (6.1).

Зная функцию распределения F(x) непрерывной случайной величины, плотность распределения в точках непрерывности F(x)можно вычислить по формуле:

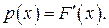(6.2)

Если Х – непрерывная случайная величина, то вероятность того, что она принимает значения из полуинтервала [x₁;x₂) вычисляется по формуле:

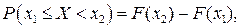(6.3)

или через плотность распределения вероятностей:

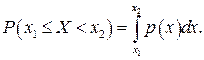(6.4)

Математическое ожидание и дисперсия непрерывной случайной величины:

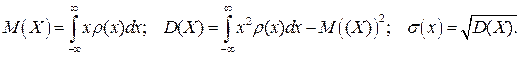(6.5)

Модой непрерывной случайной величины Х называется действительное число М_о, определяемое как точка максимума плотности распределения вероятностей р(х).

Медианой непрерывной случайной величины Х называется действительное число М_e, удовлетворяющее условию Р(Х<М_e)=Р(Х>М_e), т.е. корень уравнения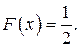

Начальный момент k-го порядка: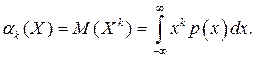

Центральный момент k-го порядка:

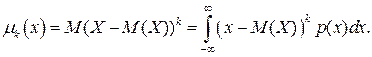
Из определения моментов следует, что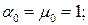

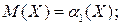
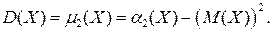
Коэффициент асимметрии или «скошенности» распределения:

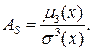
Коэффициент эксцессаили островершинности распределения:

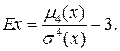
Случайная величина X называется центрированной, если М(X)=0. Если же для случайной величины X: М(Х)=0, σ(х)=1, то она называется центрированной и нормированной (стандартизованной) случайной величиной.

Задачи

6.1.Случайная величина X имеет плотность распределения вероятностей: 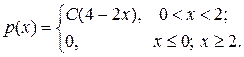Найти параметр С и функцию распределения F(x). Построить график функции распределения.

Решение. Для нахождения С воспользуемся свойством 2 плотности распределения вероятностей: 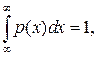т.е.

,

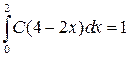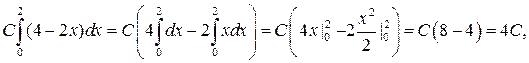
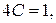откуда С=1/4.

Следовательно: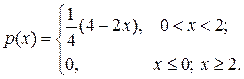

Значение функции распределения F(x) зависит от значения действительного числа х, поэтому если:

1. 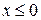,то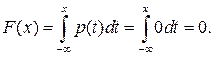

2. 0<x<2,то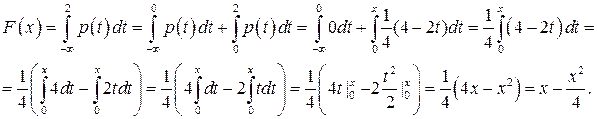

3. 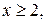то

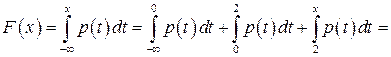
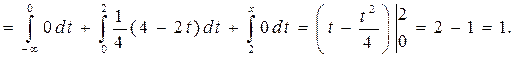
Итак,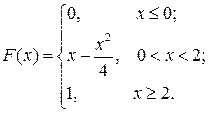

График функции распределения состоит из двух лучей y=0, y=1 и отрезка параболы 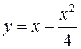и изображен на рис.6.1:

Рис.6.1

6.2.Случайная величина Х задана функцией распределения:

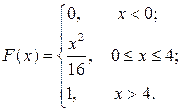
Найти плотность распределения вероятностей р(х) и вычислить вероятность того, что случайная величина Х примет значение из интервала (0;2).

Решение: Так как в точках непрерывности F(х) 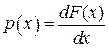, см.(6.2), то

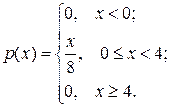
Искомую вероятность вычисляем по формуле (6.4):

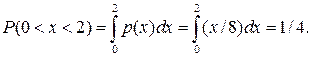
Эту вероятность можно вычислить с помощью функции распределения по формуле (6.3):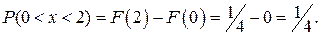

6.3.Дана функция распределения непрерывной случайной величины Х:

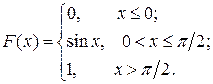
Найти плотность распределения. Построить графики р(х) и F(x).

6.4.Дана функция распределения непрерывной случайной величины Х:

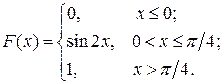
Найти плотность распределения. Построить графики р(х) и F(x).

6.5.Случайная величина задана плотностью распределения вероятностей:

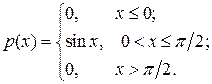
Определить математическое ожидание и дисперсию этой случайной величины.

6.6.Найти дисперсию случайной величины Х, заданной функцией распределения:

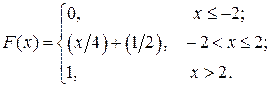
6.7.Случайная величина Х распределена по закону, определенному плотностью распределения вероятностей вида:

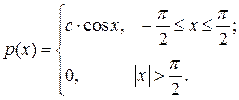
Найти константу с, определить F(х), вычислить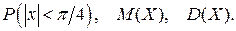

6.8.Пусть функция распределения годовых доходов лиц, облагаемых налогом равна:

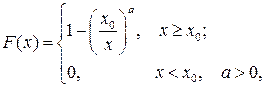
где х₀ – минимальный доход.

Определить размер годового дохода, который для случайно выбранного налогоплательщика может превзойти с вероятностью 0,5.

6.9.Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея:

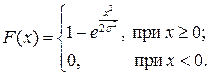
Найти: 1) плотность распределения р(х);2) медиану распределения; 3) моду распределения.

6.10.Функция распределения Вейбулла

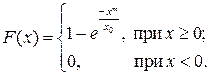
в ряде случаев характеризует срок службы электронной аппаратуры. Найти: 1) плотность распределения вероятностей; 2) моду распределения.

6.11.Случайная величина Х непрерывного типа имеет плотность распределения вероятностей изображенную на рис. 6.2.

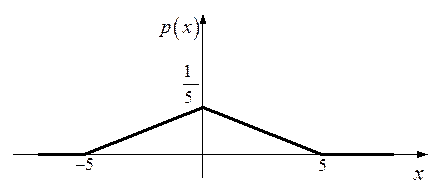
Рис.6.2

Написать аналитическое выражение для плотности р(х), вычислить функцию распределения, математическое ожидание, дисперсию, моду, медиану. Нарисовать график функции распределения.